反転を用いた東大入試の解法
反転について
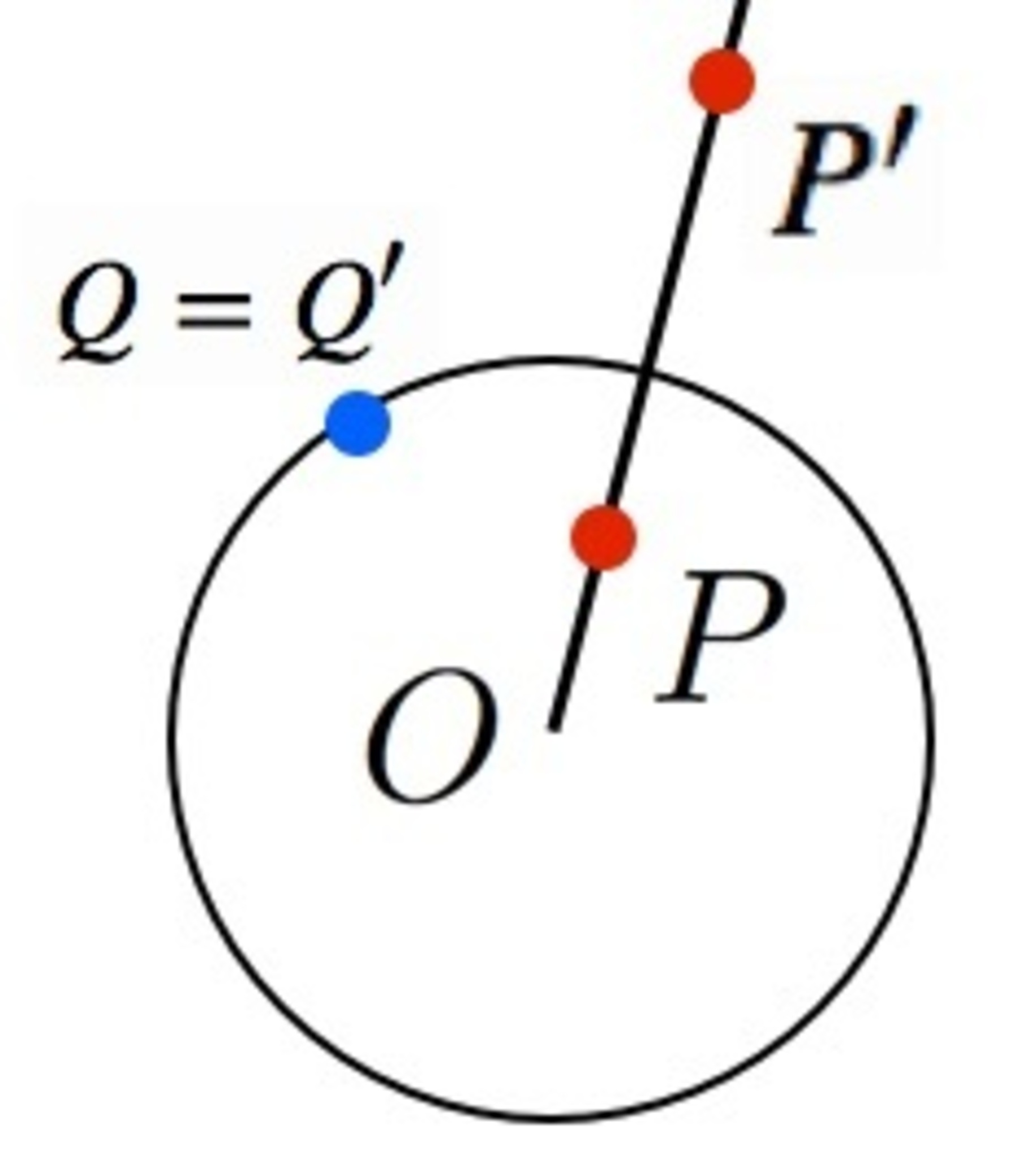
中心$O$,半径$r$の円がある.このとき,円$O$による反転を以下のように定義する.
- 点$P$の行き先は,半直線$OP$の上で$OP\cdot OP'=r^2$を満たす点$P'$.
 高校数学の美しい物語
高校数学の美しい物語
無限遠点は原点にうつるものとします.反転には以下のような性質があります.
反転によって,
$1$:原点を通る直線は原点を通る直線にうつる
$2$:原点を通らない直線は原点を通る円にうつる
$3$:原点を通る円は原点を通らない直線にうつる
$4$:原点を通らない円は原点を通らない円にうつる
複素数平面上の反転
今回は単位円での反転のみを考えるので,$r=1$とします.
複素数平面における反転は以下のように表される.
$f:\mathbb C \to \mathbb C$
\begin{align*}
f(z)=\dfrac{1}{\bar z}
\end{align*}
$z$の行き先を$\omega$とする.このとき,
\begin{align*}
|z|\cdot|\omega|=1\tag{1}
\end{align*}
また,$\omega$は半直線$OZ$上の点であることから,正の実数$t$を用いて$\omega=tz$と表される.$(1)$より,$|\omega| = \dfrac{1}{|z|}$を得る.よって,
\begin{align*}
|\omega|&=t|z|\\
&=\dfrac{1}{|z|}\\
\therefore t&=\dfrac{1}{|z|^2}
\end{align*}
よって,$\omega=\dfrac{1}{\bar z}$となる.つまり,
\begin{align*}
f(z)=\dfrac{1}{\bar z}
\end{align*}
問題
複素数平面上の原点以外の点$z$に対して$\omega=\dfrac{1}{z}$とする.
$(1)$ $\alpha$を$0$でない複素数とし,$\alpha$と原点$O$を結ぶ線分の垂直二等分線を$L$とする.点$z$が$L$上を動くとき,$\omega$の軌跡は円から一点を除いたものになる.この円の中心と半径を求めよ.
$(2)$ $1$の$3$乗根のうち,虚部が正であるものを$\beta$とする.点$\beta$と点$\beta^2$を結ぶ線分上を$z$が動くときの点$\omega$の軌跡を求め,複素数平面上に図示せよ.
解法
今回,反転させた後で工夫が必要です.$\omega=\dfrac{1}{z}$なので,単位円で反転させて得た図形を実軸で折り返すと良いです.
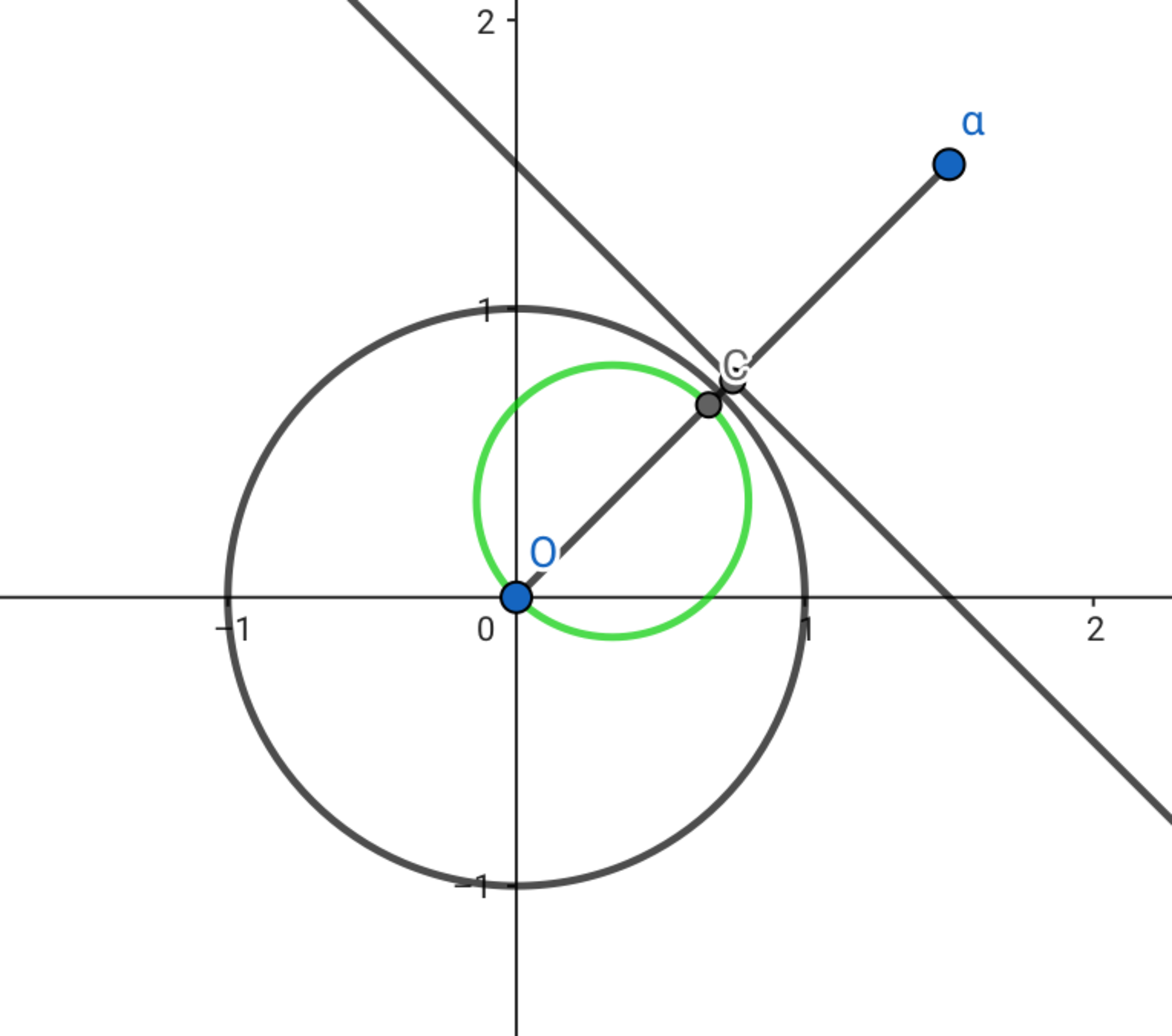
$(1)$からやりましょう.線分と垂直二等分線の交点は$\dfrac{\alpha}{2}$です.また,$L$を反転させると,原点を通る円になります.$\dfrac{\alpha}{2}$を反転させた点と原点を結んだ線分は,$L$を反転させてできる円の直径となります.これは簡単に証明できるので是非挑戦してみてください.
点$\dfrac{\alpha}{2}$の行き先は,点$\dfrac{2}{\bar\alpha}$です.この点と原点を結ぶ線分が直径となるので,反転して得た円の半径は$\dfrac{1}{|\alpha|}$,中心は$\dfrac{1}{\bar\alpha}$です.
直線$L$を反転させると,以下の図で緑色の円になります.
 反転❶
反転❶
後は実軸で折り返せば終わりです.$(1)$答は半径$\dfrac{1}{|\alpha|}$,中心$\dfrac{1}{\alpha}$の円です.
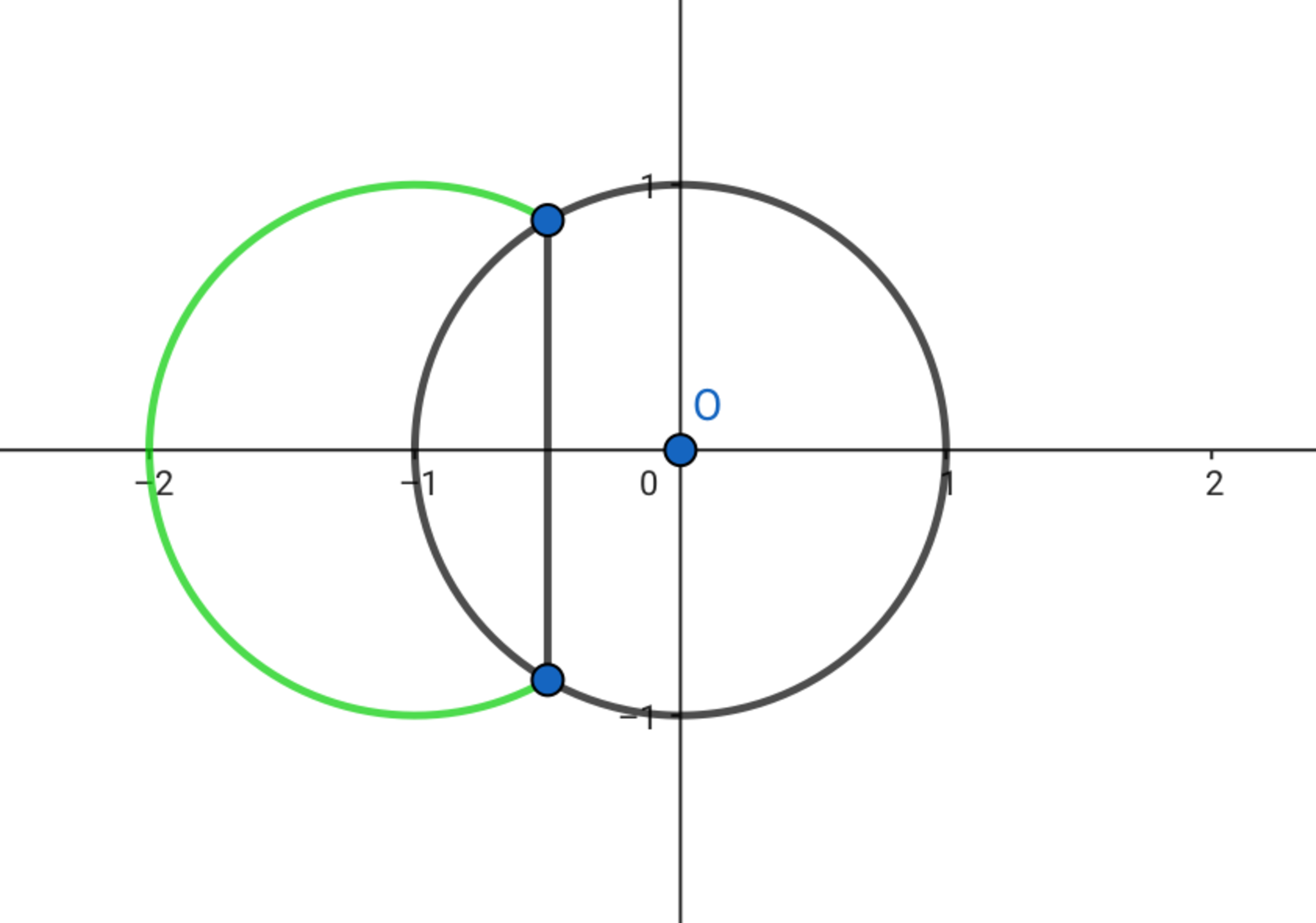
$(2)$の問題です.明らかに$ \beta=e^{\frac{\pi i}{3}}$ですね.$\beta$と$\beta^2$は共役の関係にあるので,線分は虚軸に平行です.一回反転してみると以下の図のようになります.
 反転❷
反転❷
明らかに実軸対称ですから,これが答えとなります.