文献あり

結合幾何学の紹介

227

結合幾何学とは

点と直線とこれらの接続の仕方をまとめた結合構造と呼ばれる構造を用いて行う幾何のことを結合幾何と呼び、その結合幾何について考える分野を結合幾何学と呼ぶ。
接続の仕方しか考慮しなくてよいので、結合幾何はいろいろな分野で利用されている。幾何学のほかに、例えば組合せ論や論理学などにも応用されてる。
結合構造について、詳しくはMathlogの記事結合構造基礎の基礎を参照してほしい。

定義

結合幾何（接続幾何）

結合構造$\paren{\mathcal{P},\ \mathcal{L},\ \mathcal{I}}$が次を満たすときに結合幾何と呼ぶ。

$\abs{\mathcal{P}} \geq 2$
任意の異なる点$P$, $Q$に対して、$P \in l,\ Q \in l$を満たす直線$l \in \mathcal{L}$が唯一つ存在する。
$\forall l \in \mathcal{L}$に対して、直線$l$上の点の集合$\Gamma_\mathcal{P}\paren{l}$は$\abs{\Gamma_\mathcal{P}\paren{l}} \geq 2$を満たす。
$\forall l \in \mathcal{L}$に対して、$P \notin l$となる点$P \in \mathcal{P}$が存在する。

共線的

点の集合$\mathcal{P}^\prime \subseteq \mathcal{P}$に対して、$\mathcal{P}^\prime \subseteq l$となる直線$l \in \mathcal{L}$が存在するとき、$\mathcal{P}^\prime$を共線的と呼ぶ。

平行

直線$l, m$の共通が存在しない、つまり$\abs{\Gamma_\mathcal{P}\paren{l} \cap \Gamma_\mathcal{P}\paren{m}} = 0$のとき、$l$と$m$は平行であるという。また、$l$と$m$は平行であるとき$ l \parallel m$と書く。

直線の交点

直線$l, m$の共通が一点しかない、つまり$\abs{\Gamma_\mathcal{P}\paren{l} \cap \Gamma_\mathcal{P}\paren{m}} = 1$のときにその点を$l$と$m$の交点と呼ぶ。また、交点が$A$のとき$l$と$m$は交点$A$で交わるという。

略記

異なる点$A,\ B \in \mathcal{P}$を通る直線を$\lrvec{AB}$と書く。
結合幾何の定義より$\lrvec{AB}$が表す直線は一意に決まる。

具体例

ここでいくつか具体例を見ていく。

ユークリッド平面 $\R^2$

$\mathcal{P} = \R^2$, $\mathcal{L} = \bigcup_{a,b \in \R}\toset{\paren{x,\ y}}{y = ax + b} \cup \bigcup_{a \in \R}\toset{\paren{x,\ y}}{x = a}$, $\mathcal{I} = \mathcal{P} \times \mathcal{L}$とする。
このとき結合構造$\R^2 = \paren{\mathcal{P},\ \mathcal{L},\ \mathcal{I}}$は結合幾何になる。この結合幾何をユークリッド平面と呼ぶ。

位数$3$の有限アフィン平面 $\mathcal{A}_3$

$\mathcal{P} = \brace{A,\ B,\ C,\ D,\ E,\ F,\ G,\ H,\ I}$, $\mathcal{L} = \brace{\brace{A,\ B,\ C},\ \brace{D,\ E,\ F},\ \brace{G,\ H,\ I},\ \brace{A,\ D,\ G},\ \brace{B,\ E,\ H},\ \brace{C,\ F,\ I},\ \brace{A,\ F,\ H},\ \brace{B,\ D,\ I},\ \brace{C,\ E,\ G},\ \brace{A,\ E,\ I},\ \brace{B,\ F,\ G},\ \brace{C,\ D,\ H}}$, $\mathcal{I} = \mathcal{P} \times \mathcal{L}$とする。
このとき結合構造$\mathcal{A}_3 = \paren{\mathcal{P},\ \mathcal{L},\ \mathcal{I}}$は結合幾何になる。この結合幾何を位数$3$の有限アフィン平面と呼ぶ。

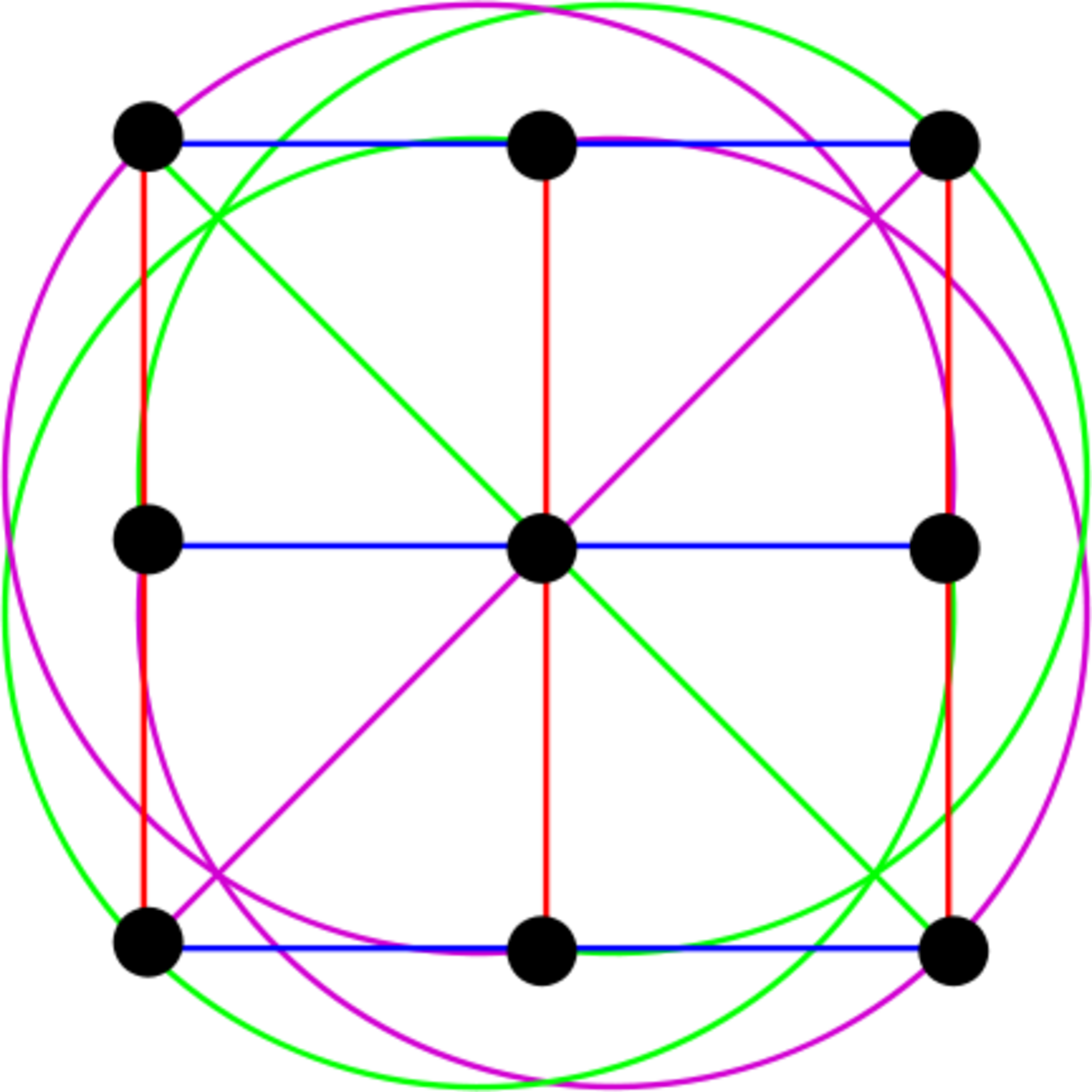9点と12直線を持つ位数3の有限アフィン平面の図。同じ色の「直線」は「平行」の関係にある Wikipediaの有限幾何学>有限平面>有限アフィン平面参照

位数$2$の有限射影平面 $\mathcal{P}_2$

$\mathcal{P} = \brace{A,\ B,\ C,\ D,\ E,\ F,\ G}$, $\mathcal{L} = \brace{\brace{A,\ B,\ E},\ \brace{E,\ F,\ G},\ \brace{A,\ C,\ G},\ \brace{B,\ C,\ F},\ \brace{A,\ D,\ F},\ \brace{B,\ D,\ G},\ \brace{C,\ D,\ E}}$, $\mathcal{I} = \mathcal{P} \times \mathcal{L}$とする。
このとき結合構造$\mathcal{P}_2 = \paren{\mathcal{P},\ \mathcal{L},\ \mathcal{I}}$は結合幾何になる。この結合幾何を位数$2$の有限射影平面と呼ぶ。また、この位数$2$の有限射影平面はファノ平面（Fano plane）としてよく知られている。

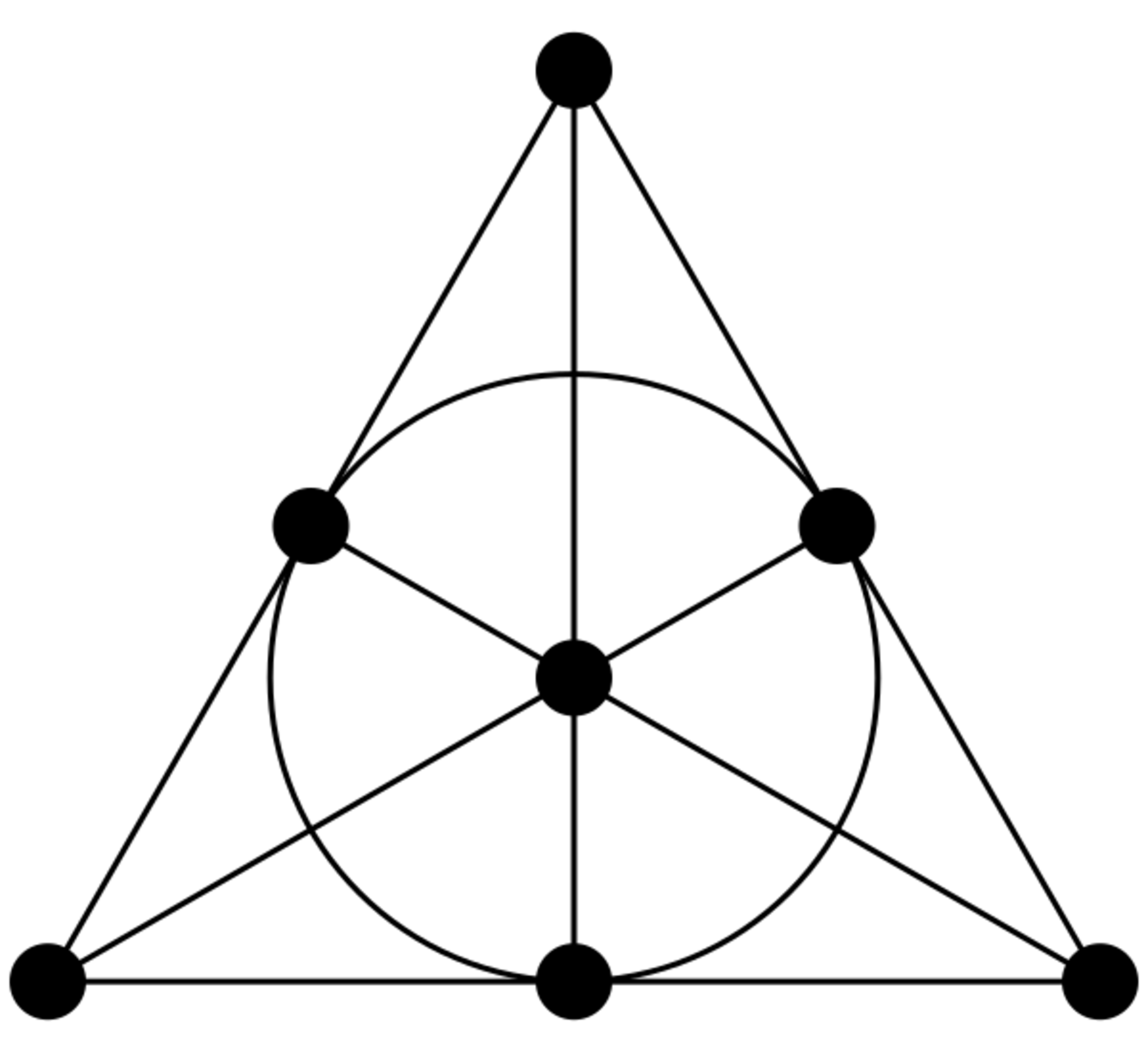7点と7直線を持つファノ平面の図 Wikipediaの有限幾何学>有限平面>有限射影平面参照

$2$-$\paren{v,\ k,\ 1}$デザイン

$v,\ k$を$v \geq k \geq 0$を満たす整数とする。
$\mathcal{P}$と$\mathcal{L}$を次の条件を満たすように作る。

$\abs{\mathcal{P}} = v$
任意の$l \in \mathcal{L}$に対し、$\abs{\Gamma_{\mathcal{P}}\paren{l}} = k$
任意の異なる$A,\ B \in \mathcal{P}$に対し、$A$と$B$を共に通る直線$l \in \mathcal{L}$が唯一つ存在する。

このとき、$\paren{\mathcal{P},\ \mathcal{L},\ \mathcal{P} \times \mathcal{L}}$は結合幾何となる。この結合幾何を$2$-$\paren{v,\ k,\ 1}$デザインと呼ぶ。
実は、$2$-$\paren{n^2,\ n,\ 1}$デザインは位数$n$のアフィン平面となり、$2$-$\paren{n^2+n+1,\ n+1,\ 1}$デザインは位数$n$の射影平面になるが、ここでは詳しく説明しない。
（詳しくは Wikipediaのブロックデザイン参照）

練習問題

相異なる点$A$, $B$, $C$において次は同値。

点$C$は直線$\lrvec{AB}$上にない
点$A$は直線$\lrvec{BC}$上にない
点$B$は直線$\lrvec{AC}$上にない
3点$A$, $B$, $C$を同時に通る直線は存在しない（$A$, $B$, $C$は共線的ではない）

1=>2=>3=>1を示すことができれば4と1が同値であることがすぐわかる。

まず1=>2を示す。
もし$A \in \lrvec{BC}$だとすると、三点$A$, $B$, $C$は共線的である。つまり、$C \in \lrvec{AB}$なので1より矛盾。よって1=>2が成り立つ。
2=>3, 3=>1も同様に示すことができる。$\QED$

任意の点に対してその点で交わる直線が少なくとも2本存在する。

任意の点を$P \in \mathcal{P}$とする。
$\abs{\mathcal{P}} \geq 2$より$P$と異なる点を取ることができるので、その点を取り$Q$とする。さらに任意の直線に対して直線上にない点が取れるので$\lrvec{PQ}$上にない点を$R$とする。
いま、$\lrvec{PQ} = \lrvec{PR}$とすると$R \in \lrvec{PQ}$であるが、$R$の取り方から$R \notin \lrvec{PQ}$なので矛盾する。よって$\lrvec{PQ} \neq \lrvec{PR}$となり、点$P$を通る直線が2本取れた。$\QED$

任意の点に対してその点を通らない直線が存在する。

任意の点を$P \in \mathcal{P}$とする。
$\abs{\mathcal{P}} \geq 2$より$P$と異なる点を取ることができるので、その点を取り$Q$とする。さらに任意の直線に対して直線上にない点が取れるので$\lrvec{PQ}$上にない点を$R$とする。
ここで$R \notin \lrvec{PQ}$と問題１より、$P \notin \lrvec{QR}$が成り立つ。よって、点$P$を通らない直線として$\lrvec{QR}$が取れた。$\QED$