9
解説競技数学
市松模様テクニック
$$$$
0.市松模様とは
市松模様
こんな感じの模様です。
1.有名なテクニック
問題$1$
$10×10$のマス目をT型テトロミノで敷き詰められない事を示せ。
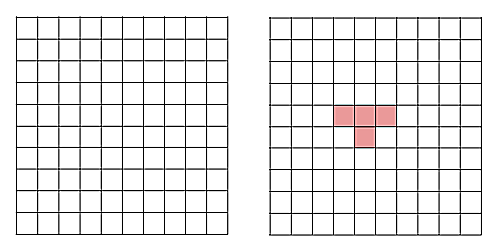Tmino
背理法で示します。
マス目を白と青の市松模様に塗ると、T型テトロミノ(以下T)を置いた時、
①白$1$マス、青$3$マスにかかる
②青$3$マス、白$1$マスにかかる
のどちらかになります。
Tichimatu
盤面の白と青の個数は同じなので、
①を満たすTと②を満たすTの個数は等しくなければいけません。
しかし、Tの個数は$25$個なのでそんなことはありえません。
よって背理法により示されました。
2.さらなるテクニック
問題2
$10×10$のマス目をI型テトロミノで敷き詰められない事を示せ。
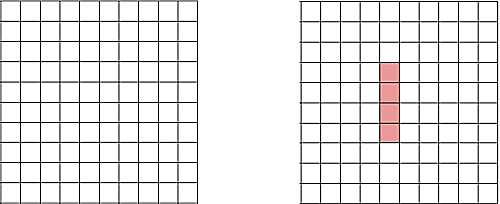Imino
これも背理法で示します。
マス目を市松模様を$2$倍に引きのばしたように塗ります。
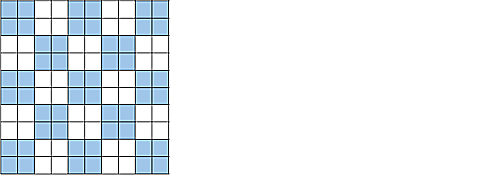bigichimatu
I型テトロミノを置くと、必ず白$2$マス、青$2$マスにかかります。
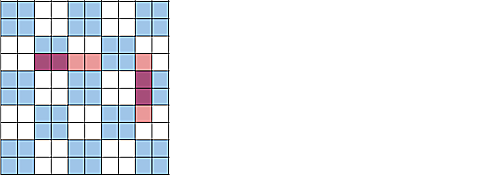Ioki
白いマスは$48$マスしかないのでI型テトロミノは$24$個より多く置けません。
しかし、I型テトロミノは$25$個置かなければならないので矛盾します。
よって背理法により示されました。
3.おわりに
何かこれだけじゃ物足りないので、最後にかなり難しめの自作問題を出します。(というか、今までのが前座です)
問題3
$3×6$のマス目を白と黒で塗ります。その塗り方のスコアを、
$2^p$ $(p=(白の連結成分の個数)+(黒の連結成分の個数))$とします。
この時、塗り方2^18通り全てのスコアの和を求めてください。
(例)下の図の場合、白の連結成分は$3$つで、黒の連結成分も$3$つなのでスコアは$64$です。
36
解答は載せません。
投稿日：2020年11月10日
更新日：2021年11月9日
投稿者
投稿者
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
コメント
コメント