歴史上の数学者さん達とコラボしてみた(*´∀｀*)

ガリレオシーケンス

・ガリレオ featuring みゆ
ガリレオ
みゆれお
$$\frac12=\frac{1+2+3}{3+4+5}=\frac{1+2+3+4+5}{4+5+6+7+8}=\frac{1+2+3+4+5+~6~+~7~}{5+6+7+8+9+10+11}=\cdots$$

$$\\[8pt]$$

二平方恒等式

・ディオファントス featuring みゆ
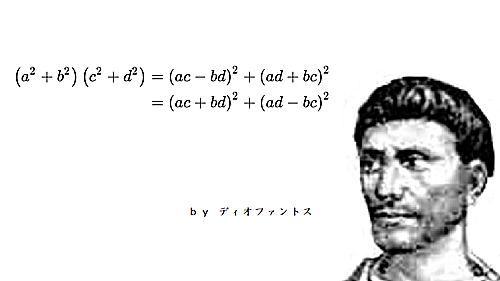ディオファントス
みゆふぁんとす
$$\begin{align} &(a^2+b^2-2ab\cos\theta)(c^2+d^2-2cd\cos\theta)\\ =&(ac-bd)^2+(ad+bc-2bd\cos\theta)^2-2(ac-bd)(ad+bc-2bd\cos\theta)\cos\theta\\ =&(ad-bc)^2+(ac+bd-2bc\cos\theta)^2-2(ad-bc)(ac+bd-2bc\cos\theta)\cos\theta\\ \end{align}$$

$$\\[8pt]$$

円周率を求める公式

・マチン featuring みゆ
マチン
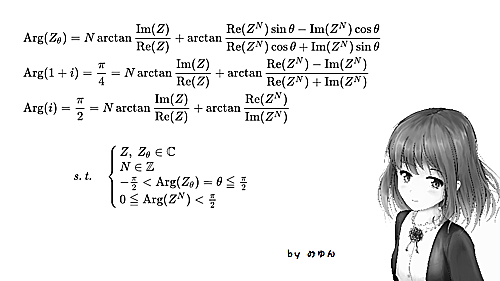みゆん
$$\begin{align} &\mathrm{Arg}(Z_\theta)=N\arctan\frac{\mathrm{Im}(Z)}{\mathrm{Re}(Z)}+\arctan\frac{\mathrm{Re}(Z^N)\sin\theta-\mathrm{Im}(Z^N)\cos\theta}{\mathrm{Re}(Z^N)\cos\theta+\mathrm{Im}(Z^N)\sin\theta}\\ &\mathrm{Arg}(1+i)=\frac{\pi}4=N\arctan\frac{\mathrm{Im}(Z)}{\mathrm{Re}(Z)}+\arctan\frac{\mathrm{Re}(Z^N)-\mathrm{Im}(Z^N)}{\mathrm{Re}(Z^N)+\mathrm{Im}(Z^N)}\\ &\mathrm{Arg}(i)=\frac{\pi}2=N\arctan\frac{\mathrm{Im}(Z)}{\mathrm{Re}(Z)}+\arctan\frac{\mathrm{Re}(Z^N)}{\mathrm{Im}(Z^N)}\\\\ &\mathit{s.t.}\quad\begin{cases} Z,\ Z_\theta\in\mathbb{C}\\ N\in\mathbb{Z}\\ -\frac\pi2\lt\mathrm{Arg}(Z_\theta)=\theta\leqq\frac\pi2\\ 0\leqq\mathrm{Arg}(Z^N)\lt\frac\pi2 \end{cases} \end{align}$$

$$\\[8pt]$$

極座標と直交(斜交)座標の関係式

・オイラー featuring みゆ
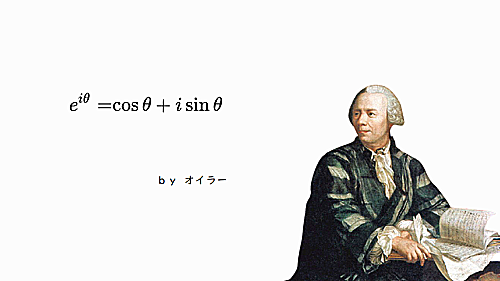オイラー
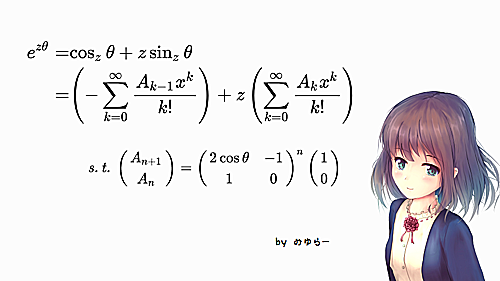みゆらー
$$\begin{align} e^{z\theta}=&\cos_z\theta+z\sin_z\theta\\ =&\left(-\sum_{k=0}^\infty\frac{A_{k-1}x^k}{k!}\right)+z\left(\sum_{k=0}^\infty\frac{A_{k}x^k}{k!}\right)\\\\ &\mathit{s.t.}\quad \begin{pmatrix}A_{n+1}\\A_n\end{pmatrix}=\begin{pmatrix}2\cos\theta&-1\\1&0\end{pmatrix}^n\begin{pmatrix}1\\0\end{pmatrix} \end{align}$$

$$\\[8pt]$$

立方和の恒等式

・ラマヌジャン featuring みゆ
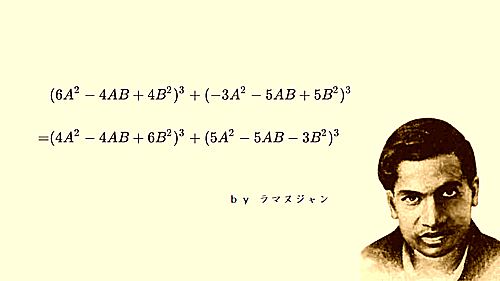ラマヌジャン
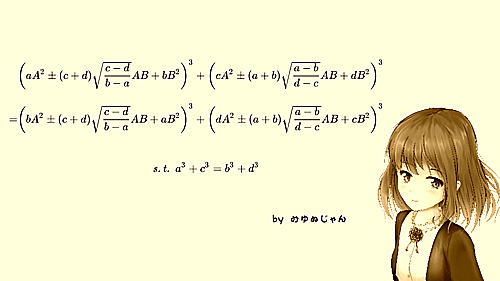みゆぬじゃん
$$\begin{align} &\left(aA^2\pm(c+d)\sqrt{\frac{c-d}{b-a}}AB+bB^2\right)^3+\left(cA^2\pm(a+b)\sqrt{\frac{a-b}{d-c}}AB+dB^2\right)^3\\ =&\left(bA^2\pm(c+d)\sqrt{\frac{c-d}{b-a}}AB+aB^2\right)^3+\left(dA^2\pm(a+b)\sqrt{\frac{a-b}{d-c}}AB+cB^2\right)^3\\ \\ &\mathit{s.t.}\quad a^3+c^3=b^3+d^3\\ \end{align}$$