底が負の指数関数、対数関数を定義したい記事

底が負の指数関数や対数関数について

皆さん、突然ですが底が負の指数関数や対数関数を定義してみたいと思ったことはありませんか？
ありますね？あるに決まっています。(圧)

そこでこの記事では、底が負の指数関数、対数関数を定義して、性質について調べてみたいと思います。

指数関数の定義

底を$a(a<0,a≠-1)$とすると
$ f(x)=a^{x} =(-1)^{x}(-a)^{x} =e^{(2n-1) \pi ix}(-a)^{x} (n \in \mathbb{Z}) $
よって
$$ Re(f(x))=(-a)^{x} \cos(2n-1)πx $$
$$ Im(f(x))=(-a)^{x} \sin(2n-1)πx $$
ここで、$f(x)$は実変数複素関数であるためギリギリ3次元で描画できます。
そこで、この式をもとに我らがdesmos様に描画していただきましょう。
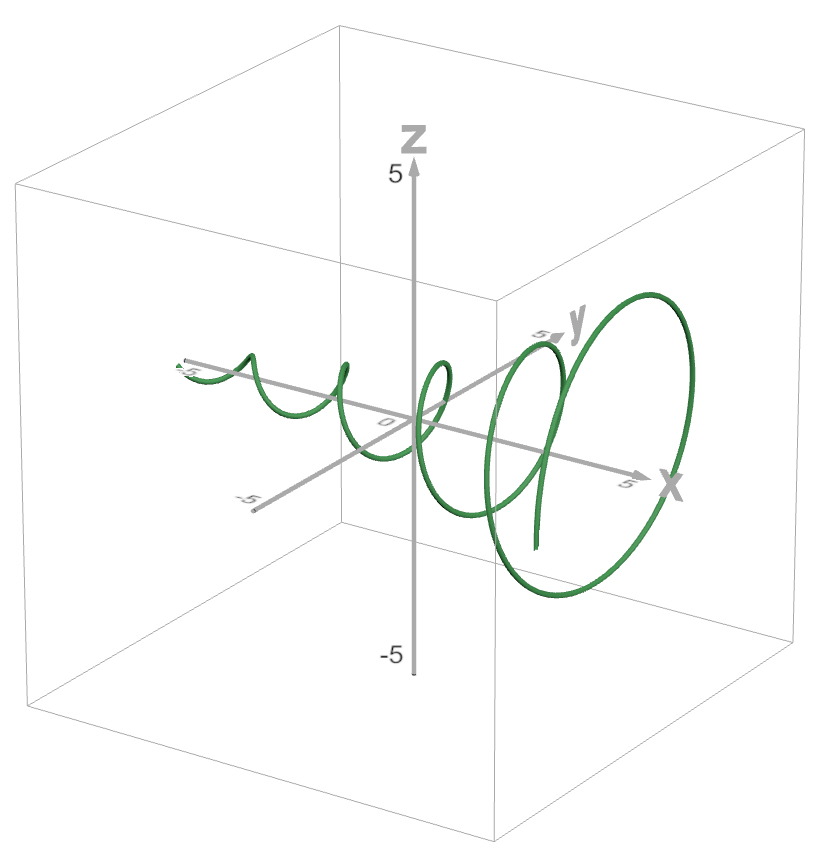n=1のみの図
螺旋型になっていますね。
$x$軸からの距離が$a^{x}$で偏角が$(2n-1)\pi x$の点が集まっているので、$x$が増えるにつれて幅が広がっていっています。
実際には$n$がたくさんあるので、下の図のようになります。
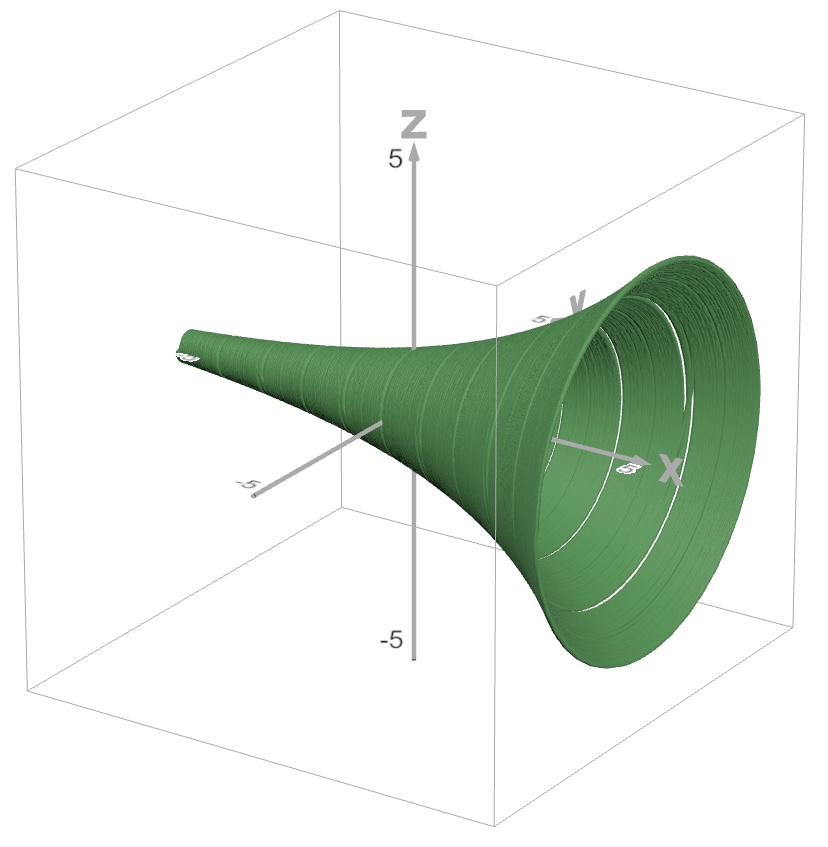nをたくさんにした図
ラッパのような形をしていますね。
よく見るとところどころ線が無いところがありますが、
これはxが整数のとき$e^{(2n-1)iπ}=-1$であるため、その部分だけ点がf(x)=1に集まるためです。
(これがこの後対数関数を定義するときに悪さします。)
よく、底が負の指数関数のグラフというと
$y=±a^x$の格子点のみをプロットしたものを浮かべることが多いと思いますが、
実は3次元の螺旋になっていたんですね。
(この螺旋の実部を切り取るとそのようなグラフになっています。)

対数関数の定義

これは、先程のグラフで複素平面上のとある点からx軸に平行に直線を引き、ラッパとの交点のx座標で定義できます。
とある条件を満たす(後述)複素数zがどのxで交点をもつかを考えると、
$|z|=|a|^{x}$より両辺底が$|a|$の対数をとって
$\log_{|a|}|z|=x$
という形で定義される、
と言いたい所ですが、先程の条件というものについて考えていきます。

指数関数のグラフのときに言及した、線が無い部分について、実は$x$が整数のときだけでなく$x$が有理数の時にもまた線がなくなります。
x=1.2のときの図
なぜなら、$x$が有理数のとき$x=p/q$とすると
$f(x)=e^{(2n-1)iπ･p/q}$
であり$n=m+q$とすると、
$e^{(2(m+q)-1) \pi i·p/q}=e^{(2m-1) \pi i·p/q+2p\pi i}$
より、$q$周期でプロットした点が重なるため線でなくなります。

よって、$\log_{|a|}|z|=x$が有理数で$z$の偏角$arg(z)$が$(2k-1)\pi p/q (k \in \mathbb{Z})$でないとき$z$に対応する$x$が存在しません。

これが先程言及した条件で、底が負であるとき対数関数は式にすると
$\log_{|a|} |z| \notin \mathbb{Q}$
$\log_{|a|}|z|=x$が有理数である場合は、
$x=p/q$とおくと
$arg(z)=(2k-1)\pi p/q (k \in \mathbb{Z})$
のときに$\log_{a}z$が存在し$\log_{|a|}|z|$をとる。
まとめると、底が負の対数関数の存在条件は
$\log_{|a|}|z| \notin \mathbb{Q}$または$arg(z)=(2k-1)\pi p/q (k \in \mathbb{Z},x=p/q)$のとき
であるとわかります。

性質を確かめてみる

底が正のときに成り立っていた指数法則や対数の性質は底が負でも成立にしているのか確かめてみましょう。

指数法則

$ \begin{eqnarray} \left\{ \begin{array}{l} A^{n} A^{m}= A^{n+m} & (A \lt0) &\cdots \spadesuit \\ \displaystyle \frac{A^{n}}{A^{m}}=A^{n-m}&(A\lt 0) &\cdots \heartsuit \\ A^{n}B^{n}=(AB)^{n}&(A,B\lt0) &\cdots \diamondsuit \\ (A^{n})^{m}=A^{nm} &(A\lt0) &\cdots \clubsuit\\ \end{array} \right. \end{eqnarray} $
が成り立っていることを確かめます。

$\spadesuit$については
$ \begin{align*} A^{n}A^{m} &=(-A)^{n}(-A)^{m}e^{(2k-1)\pi in}e^{(2k-1)\pi im}\\ &=(-A)^{(n+m)}e^{(2k-1)\pi i(n+m)}\\ &=A^{(n+m)} \blacksquare \end{align*} $

$\heartsuit$も同様です。

$\diamondsuit$については
$\begin{align*} A^{n}B^{n}&=(-A)^{n}(-B)^{n}e^{(2k-1)\pi in}e^{(2k-1)\pi in}\\ &=(AB)^{n}(-1)(-1)\\ &=(AB)^{n}\blacksquare \end{align*}$

$\clubsuit$についても
$\begin{align*} (A^{n})^{m}&=((-A)^{n})^{m}(e^{(2k-1)\pi in})^{m}\\ &=(-A)^{nm}e^{(2k-1)\pi inm}\\ &=A^{nm}\blacksquare \end{align*}$

というように、底が負でも指数法則は成り立つようです。

対数法則

底が正のときと同様に指数法則から導けますが、底が負の場合では値が存在しない場合があり非常に面倒くさいので今回は割愛します。

まとめ

今回は指数関数や対数関数の底を負に拡張してみました。
それぞれのグラフは3次元空間で螺旋の集合体として描画されていて、個人的にすごく面白い結果となっていて満足しています。
読んでいただきありがとうございました。
描画に使ったdesmosのリンクも貼っておきます。
指数関数