ハンターと見えないうさぎを解いてみた
この記事は9割以上が以下の問題のネタバレによって構成されています.
- JMO春合宿2022 第12問(2021 IMO Shortlist C6)
- IMO2017 第3問
12月11日,
Advent Math Calendar2023
11日目です. 私は最近解けた(と思う)ハンターと見えないうさぎ問題の解答を書いてみます. 両方とも今まで解いた中でかなり好きな部類に入っています.
ちなみにMathlog初投稿です. 読みづらい箇所が多いかもしれませんがどうぞお付き合いください.
JMO春合宿2022 第12問(2021 IMO Shortlist C6)
ハンターと見えないうさぎが無限に広がるマス目でゲームをする. はじめハンターは正整数 $k$ を選び, 各マスに $k$ 以下の正整数を書き込み, うさぎと共有する. うさぎはあるマスに潜んだ後, 現在居るマスに割り当てられた整数をハンターに伝え, まだ訪れたことがなく, 辺を共有するマスに移動することを繰り返す. うさぎが動けなくなるか, ハンターがうさぎが最初に潜んだマスを特定できたとき, ゲームは終了する.
うさぎはハンターの行動によらずゲームが終了しないように行動し続けることは可能か.
予想としては, ハンターの方に必勝法がありそうなので, その前提で進めていく.
以下, ハンターは適当に1マスを決め, そこから右に$x$マス, 上に$y$マス進んだ所にあるマスを $(x,y)$ と呼ぶ.
問題のゲームをゲーム0 とし, ハンターが正整数$m$を選び, 各マスに$m$個の有限な正整数を順番付きで書きこめるようにルールを変更したゲームを ゲーム1 とする.
ゲーム1でハンターに必勝法があるならば, ゲーム0でもハンターに必勝法がある.
ゲーム1において, ハンターが必ず勝利できるような盤面が存在すると仮定し, そのうちの一つを$A$とする. $A$の全てのマスについて書かれた整数の最大値を$M$とする. 各マスについて書き込まれた$m$個の整数を順に$a_1,a_2,\cdots a_m$として, それを一つの整数$a_1(M+1)^{m-1}+a_2(M+1)^{m-2}+\cdots+a_m(M+1)^0$に書き換えた盤面を$B$とする. (つまり$(M+1)$進法表記として解釈する.)
$M$と$B$が与えられたとき, $A$を一意に復元することが可能であるから, $A$を用いてゲーム1をすることは$M$と$B$を用いてゲーム0をすることと等価である. よって, ゲーム1でハンターに必勝法があるならばゲーム0でもハンターに必勝法がある.
以下では, (マスに整数がいくつか書けて嬉しいので)ゲーム1でハンターに必勝法があることを示す.
各マスに$2$個の正整数を書き込んで, うさぎがそれぞれの移動でどの方向に進んだのかわかるようにできる.
マス$(x,y)$について, $x-y\pmod3$を書き込み(図A), $x+y\pmod3$を書き込む(図B)事を考える.(ただし$0$の代わりに$3$を書き込む.)
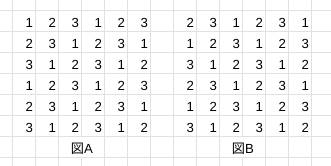
図Aに書かれた数から, うさぎが左または上か,右または下のどちらに進んだかがわかる. さらに, 図Bに書かれた数から, うさぎが右または上か, 左または下のどちらに進んだかがわかる. よって, これらを組み合わせればうさぎが各移動で上下左右のどの向きに進んだかがわかる.
ハンターはうさぎの移動の向きを知ることができることがわかった. つまり, ハンターはうさぎが今いるマスが, 最初にうさぎがいるマスから見て左右及び上下に何マス進んだ位置にあるかを常に知ることができる.
この情報を使ってうさぎがいたマスを特定していく. (感覚的なお話:上下左右のうち一つの方向には無限に進んでいくことを使って, )$x$座標または$y$座標が特定できることを示す.
ハンターはうさぎが最初にいたマスの$x$座標または$y$座標を特定可能である.
$a$を正整数とする
$x$座標が$2^a$で表せるようなマスの集合を$S_a$, $-2^a$で表せるようなマスの集合を$S_{-a+1}$とし, 全ての$a$について$S_a$の和集合を$S$, $S_{-a+1}$の和集合を$T$とする. それぞれのマスについて, $S$に属すなら$1$を, $T$ に属すなら$2$を, どちらにも属さないなら$3$を書き加える.
つぎに,$y$座標が$2^a$で表せるようなマスの集合を$U_a$, $-2^a$で表せるようなマスの集合を$U_{-a+1}$とし, 全ての$a$について$U_a$の和集合を$U$, $U_{-a+1}$の和集合を$V$とする. それぞれのマスについて, $U$に属すなら$1$を, $V$ に属すなら$2$を, どちらにも属さないなら$3$を書き加える.
任意の整数$b,c$について, $S_{b-1},S_{b+1},U_{c-1},U_{c+1}$に属すマスで囲まれた部分にあるマスの数は有限個であるため, うさぎはこの範囲だけで無限に移動を続けることはできない. よって, ある整数$b,c$について, うさぎは$S_b$に属すマスと$S_{b+1}$に属すマスの両方, または$U_c$に属すマスと$U_{c+1}$に属すマスの両方を通る.
前者の場合について考える. ハンターはうさぎが最初にいたマスからみて, うさぎが左右方向にどの向きに何マス離れたマスにいるか常に知ることができるから, うさぎが最初にいたマスの$x$座標を$X$として, 異なる整数$d,e$について$X+d$と$X+e$が, $2^a$で表せる, あるいは$-2^{a}$で表せるという情報が得られる.
このとき, $X+d$と$X+e$の間に$2^a$または$-2^a$で表せる整数は存在しないと仮定して良い.($\cdots$①)
$s,t$を非負整数とする.
- $X+d,X+e$のうち, 一方が$2^s$,もう一方が$-2^t$と表せるとき
①より$s=t=0$と定まる. よって, $X+d,X+e$のうち大きい方が$1$と等しいので, $X$は一意に定まる. - $X+d=2^s,X+e=2^t$と表せるとき
$d\neq e$より$s\neq t$である.
$d< e$であるとき, $s< t$であるから, ①より$t=s+1$. よって, $2^{s+1}-2^{s}=e-d$. つまり$2^s=e-d$.
$2^s$は狭義単調増加であるから, $s$は一意に定まる. $X=2^s-d$より, $X$も一意に定まる.
$d>e$の場合も同様に$X$は一意に定まる. - $X+d=-2^s,X+e=-2^t$と表せるとき
上と同様にして, $X$は一意に定まる.
以上より, ハンターはうさぎが最初にいたマスの$x$座標を特定できることが示された.
同様にして, $U_c$に属すマスと$U_{c+1}$に属すマスの両方を通る場合, ハンターはうさぎが最初にいたマスの$y$座標を特定できることが示される.
したがって, ハンターはうさぎが最初にいたマスの$x$座標または$y$座標を特定することが可能である.
(上下か左右のどちらかの座標がわかった. これを斜めにしたやつも重ねればマスを特定できそう. )
ハンターはうさぎが最初にいたマスの$x$座標と$y$座標の和または差を特定可能である.
$a$を正整数とする. 各マスの$x$座標, $y$座標をそれぞれ$x$,$y$と表し, うさぎが最初にいたマスの$x$座標, $y$座標をそれぞれ$X,Y$とする..
$x+y$が$2^a$と表せるようなマスの集合を$S_a$, $-2^a$で表せるようなマスの集合を$T_{-a+1}$とし, 全ての$a$について$S_a$の和集合を$S$, $S_{-a+1}$の和集合を$T$とする. それぞれのマスについて, $S$に属すなら$1$を, $T$ に属すなら$2$を, どちらにも属さないなら$3$を書き加える.
つぎに,$x-y$が$2^a$で表せるようなマスの集合を$U_a$, $-2^a$で表せるようなマスの集合を$U_{-a+1}$とし, 全ての$a$について$U_a$の和集合を$U$, $U_{-a+1}$の和集合を$V$とする. それぞれのマスについて, $U$に属すなら$1$を, $V$ に属すなら$2$を, どちらにも属さないなら$3$を書き加える.
このようにすれば, 補題3と同様にして$X+Y$または$X-Y$が特定可能であることが示せる.
ハンターはうさぎが最初にいたマスの$x$座標または$y$座標と, うさぎが最初にいたマスの$x$座標と$y$座標の和または差を特定できたので, うさぎが最初にいたマスの$x$座標と$y$座標をともに一意に特定できる. つまり, ゲーム1はハンターが必勝である.
以上より, ゲーム0ではハンターが必勝である.(終)
IMO2017 第3問
ハンターと見えないうさぎが平面上でゲームを行う. うさぎが最初にいる点$A_0$ とハンターが最初にいる点$B_0$ は一致している. $n-1$回のラウンドが終わった後, うさぎは点$A_{n-1}$ におり, ハンターは$B_{n-1}$ にいる. $n$回目のラウンドにおいて, 次の3 つが順に行われる:
(i) うさぎは$A_{n-1}$ からの距離がちょうど1 であるような点$A_{n}$ に見えないまま移動する.
(ii) 追跡装置がある点$P_{n}$ をハンターに知らせる. ただし, $P_{n}$ と$A_{n}$ の距離が1 以下であるということだけが保証されている.
(iii) ハンターは$B_{n-1}$ からの距離がちょうど1 であるような点$B_{n}$ に周りから見えるように移動する.
うさぎがどのように移動するかにかかわらず, またどの点が追跡装置によって知らされるかにかかわらず, ハンターは$10^9$回のラウンドが終わった後に必ずうさぎとの距離を$100$以下にすることができるか.
(多分, できなさそう. うさぎと追跡装置が協力すればハンターからいくらでも離れられそう.)
線分$B_nA_n$の$A_n$側の延長上に$P_{n+1}$があるとき, ハンターにとっての最善の行動は$P_{n+1}$の向きに進むことである.
$A_0=B_0=(0,0)$とする. $A_1(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}), P_1(1,0)$とすると, ハンターは$B_1(1,0)$とするのが最善. このとき, うさぎとハンターの距離は$1$.
ところで, $A_n(d,0)$,$B_n(0,0)$(ただし$1\leq d\leq 100$)とし, この時点でハンターはうさぎの位置をわかっているものとする. $m$を正整数とし, $\theta$を$\sin\theta=\dfrac{1}{m}$となる実数とする. $1\leq k\leq m$を満たす正整数$k$について, $A_{n+k}(d+k\cos\theta,k\sin\theta)$,$P_{n+k}(d+k\cos\theta,0)$とする. このとき, ハンターの最善の動きは$B_{n+k}(k,0)$とすることであり, そのように動けば$A_{n+m}(d+\sqrt{m^2-1},1)$,$B_{n+m}(m,0)$となっている. このとき, $(A_{n+m}B_{n+m})^2=(d-m+\sqrt{m^2-1})^2+1$である. $l=m-\sqrt{m^2-1}$とおくと, $(A_{n+m}B_{n+m})^2=(d-l)^2+1$と表せる.
ここで, $l\leq\dfrac{1}{4d}$となる場合を考える.
$(A_{n+m}B_{n+m})^2=(d-\dfrac{1}{4d})^2+1=d^2+\dfrac{1}{2}+\dfrac{1}{16d^2}$より, $(A_{n+m}B_{n+m})^2-(A_nB_n)^2\geq\dfrac{1}{2}$.
また, $l=m-\sqrt{m^2-1}$より$m-\sqrt{m^2-1}\leq\dfrac{1}{4d}$. これを$m$について解いて, $m\geq2d+\dfrac{1}{8d}$. $1\leq d\leq 100$より, $m\geq201$であればこれは常に満たされる.
以上より, 任意の正整数$n$について, $A_nB_n\leq100$であるならば$(A_{n+201}B_{n+201})^2-(A_nB_n)^2\geq\dfrac{1}{2}$となるようにうさぎは行動できる.
$(A_1B_1)^2\geq1$となるよううさぎは行動できるから, $(A_{(201\cdot19999+1)}B_{(201\cdot19999+1)})^2\geq1+19999*\dfrac{1}{2}=10000.5$となるようにできる.
$201\cdot19999+1<10^9$より, うさぎは$10^9$回の行動の後にハンターとの距離が$100$より大きくすることができる. つまり, ハンターは$10^9$回のラウンドが終わった後に必ずうさぎとの距離を$100$以下にすることはできない. (終)
感想など
両方とも最小値を求める問題じゃなくてよかった. 結局どちらも有限回で終わるらしいが, $1$秒に$1$回行動したとして$10$億回行動すれば$32$年になるらしい. うさぎの平均寿命は$8$年, 人間の平均寿命は$80$年くらいらしいので, 終わる前にうさぎが亡くなりそう. そもそも, 無限に広がるマス目だったり, 無限に広がる平面だったり, ここは地球上ではないのかもしれない...
将来, 万が一ハンターとうさぎの問題がShortlistとかで出たら追記するか, 別の記事を書くことにします. かなり変な記事になりましたが, 最後までお付き合いいただきありがとうございました!