コラッツの予想の証明

要約

　
コラッツ予想は任意の自然数nを「偶数なら2で割り、奇数なら３倍して１を足す」という操作を有限回繰り返すと、必ず１になるという予想である。
思うにこの証明を困難にしているのは「偶数なら２で割り」という部分であると考える。この操作は連続で生じることもあれば、１回で終わることもある。何回目の操作において何回連続でこの操作が生じるかは、手順に従って計算を繰り返してゆく他、我々がそれを知る有効な算術が存在しない。確かに、初期値を設定し、個々にそれを計算してゆく過程で、神出鬼没にすら思える「2で割る操作の連続性」を織り込んだ計算方法を一般化するのは困難である。しかしそれを織り込んだ上で「コラッツ予想の計算手順の果てが１に収束する」ことの証明は可能である。
この証明を可能にするために私は偶数について２で割る操作を、その連続回数に関わらず全て１回とみなして考える方法を採用した。これによってコラッツ計算に一定の規則性が付与され、結果的に初期に設定した任意の自然数を証明可能な形に持ってゆくことが可能となる。
尚この先数式には順に（eq)で番号を振り、その他の必要な前提事項には(ag)として番号を振ってゆく。

1定義

1コラッツ計算における数値の動きと記号の定義

ここでは証明を進めるうえで必要な記号とその記号が意味する表の上での位置などを定義する。コラッツ予想が示す計算手順（以降「手順」と記す）を遂行する過程で生じる数の並びを表にまとめると（表-1)のようになる。
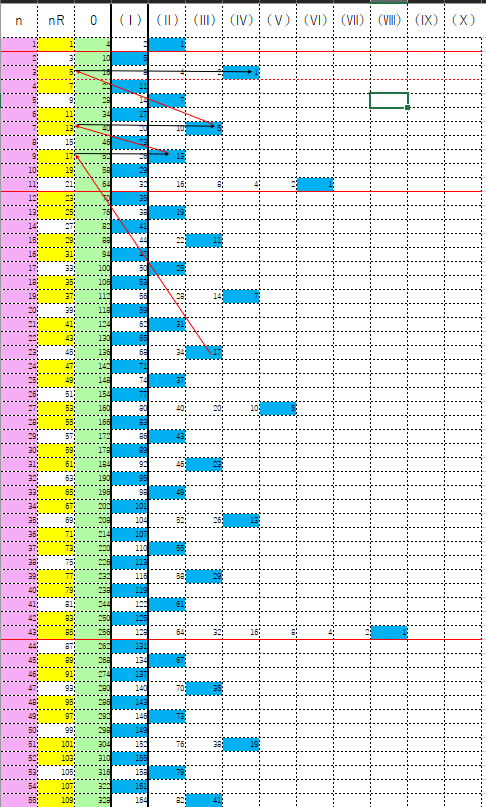表-1

1. 表の横の並びを行、縦の並びを列と呼ぶ
2. 任意に選択できる初期値を$\varDelta$$\lbrace \varDelta \in \mathbb{Z} \vert \varDelta \gt 0 \rbrace$と表す。
3. 奇数の時に行う３倍して1を足す操作をA操作とし、Aと表記する。
4. 偶数の時に行う２で割る操作をB操作とし、Bと表記する。
5. 0，Ⅰ、Ⅱ、Ⅲ、...と続く列を一般にNと表記する。
6. 手順によって算出された数値をZとし、そのZがどの列に存在するかを表すために$Z_{N}$を用いる。存在する列が明らかな場合は、例えば0列に存在するならば$Z_{0}$と表記する。更に実際の数値を入れて$52_{0}$などと書くこともあり、これは0列の数値52を示している。
7. Bによって最終的に奇数となった値を終止と呼び、$EZ_{N}$と表記する。$EZ_{N}$はそれがどの列の存在するか明らかな場合は、例えば終止がⅡ列上にある場合は$EZ_{2}$と書く。さらには実際の数値を入れて$E17_{1}$などと表すこともあり、これはⅠ列の終止17を示している。
8. $\varDelta$が偶数の場合Bによって最初に到達した$EZ_{N}$を他の$EZ_{N}$と明確に区別するために特に$\psi$と表記する。$\varDelta$が奇数であった場合は後述する奇数の網羅性より$\varDelta$$=$$\psi$となる。したがって$\lbrace \psi \in \mathbb{Z} \vert \psi \gt 0 \vert \psi = 2n-1\rbrace$である。
9. nR列は便利のために設けた列で証明には関与しない。この列はAが行われるひとつ前の$EZ_{N}$を表しており、表を眺める際に次にどの項に移動するか目視できるように設けたものである。例えば$E17_{1}$はAによって$52_{0}$に移動するのだが、$52_{0}$の同一行のnR列は17となっている。
10. 0列は$EZ_{N}$からAによって数値が移動してくる列であり、奇数を3倍して1を足したものである。奇数を2n-1とすると$Z_{0}$$=$3(2n-1)+1$=6n-2$である。
11. N列はBに関与した動きを示しており$Z_{1}$$=$$\frac{ Z_{0} }{2}$,$Z_{2}$$=$$\frac{ Z_{1} }{2}$,$Z_{3}$$=$$\frac{ Z_{2} }{2}$,$\cdots$なので
    $$ Z_{N}=\frac{3n-1}{ 2^{N-1} } $$
    (eq-1)
    である。ただし命題に準拠し表中では$Z_{N}$$\in$$\mathbb{Z}$となるものだけを表示し、それ以外のものは数値としては存在しても空欄としてある。
12. ＜表-1＞中の赤い矢印はAによる移動を、青い矢印はBによる移動を示している。本稿ではコラッツ計算による数値の動きをこのように捉える。
13. 表中の奇数に３の倍数は存在しない。これはコラッツ計算過程で、Bの計算途中以外で3の倍数は出現しないということである。これはAにより３の倍数に１を足すことで３の倍数が排除され、続くBでは２で割る操作を行うのだが、２と３は互いに素であるので３の倍数が復活することはない、ということに由来している。もちろん$\varDelta$に関しては３の倍数を選択しても構わないのだが、１回目のAでこれが排除されて以降は３の倍数に戻ることはない（ag-1)

2補題

2-1.$\boldsymbol{ pk }$について

手順によって最終的に$\varDelta$が１に収束するには、先ず$Z_{0}$$=$$2^{t}$$\times$1$\lbrace t \in \mathbb{Z} \vert t \gt0 \rbrace$に到達する必要がある。これはBによって最終的に1まで到達する項であり、例えばn$=$3の16→8→4→2→1などのことである。このような$Z_{0}$を特に$pkZ_{0}$と表すことにする。$pkZ_{0}$が現れる項数は1,3,11,43,171,683,...でありこれは階差数列として認識できる。$pkZ_{0}$が現れる項数を$pkn_{0}$とすると。
$$ pkn_{0} = 1+\sum_{j=1}^{n-1}2 \times 4^{j-1} = \frac{1}{6}( 2^{2n} +2) $$
と表され、$pkZ_{0}$は0列上の値であるので

$pkZ_{0}$$=$6$pkn_{0}$-2$=$$2^{2n}$
(eq-2)

2-2.コラッツ計算過程で出現する奇数の網羅性について

手順中に現れる数値は＜表-1＞中に現れる数値と同じである。ここでは任意の$N_{2N-1}$(奇数列)と$N_{2N}$(偶数列)という一組の奇数列と偶数列のペアが3の倍数を除くすべての奇数を表すことについて示す。奇数を調べることは$EZ_{N}$を調べることに他ならない。（※これを示すのは、全ての初期値が最終的に1に収束することを示すのがコラッツ予想の命題であるから、表中の数値を用いて証明するのに、そこに存在しない奇数があってはそもそもの前提が崩れてしまうからである）

$EZ_{N}$が奇数列に含まれる項はⅠ列目は2n,Ⅲ列目は8n-1,Ⅴ列目は32n-5,Ⅶ列目は128n-21,...
これらはnの係数項と定数項に分けることによって以下のように規則性を見出せる。

$$ 係数項＝2^{N}n $$

$$ 定数項＝\frac{1}{12} \left( 4^{n} -4 \right) $$
定数項の次数nはⅠ列目を1、Ⅲ列目を2、Ⅴ列目を3，...と数えたのもの、即ち奇数列のみで考えたた場合の列順番号です。よって以下のように書き直す
$$ \frac{1}{12} \left( 4^{ \frac{N}{2}+ \frac{1}{2} }-4 \right) $$
これでⅠ列目を1、Ⅲ列目を3、Ⅴ列目を5，...と数えたのものに変換できたことになります。以上より奇数列に$E_{Z}$が現れる項数は
$2^{N}n$$-$$\frac{1}{12}$($4^{ \frac{N}{2}+ \frac{1}{2} }$$-4$)
(eq-3)
$E_{Z}$の内奇数列に現れるものを$ \widehat{E} _{Z}$とし、（eq-3)を(eq-1)のｎに代入すると
$ \widehat{E} _{Z}$=$\frac{1}{ 2^{N-1} }$$\lbrack 3 \lbrace 2^{N}n- \frac{1}{12} \left( 4^{ \frac{N}{2}+ \frac{1}{2} }-4 \right) \rbrace-1 \rbrack$
これを整理すると
$ \widehat{E} _{Z}$$=6n-1$
(eq-4)
同様に偶数列も考えて
$EZ_{N}$が偶数列に含まれる項はⅡ列目は4n-3,Ⅳ列目は16n-13,Ⅵ列目は64n-53,Ⅷ列目は256n-213,...
係数項は奇数列の場合と同じであるので、定数項を考えると
$\frac{1}{6}$(5$\times$$4^{ \frac{N}{2} }$$-2$)
$E_{Z}$の内偶数列に現れるものを$ \widetilde{E} _{Z}$とすると、奇数列の場合と同じように処理して
$ \widetilde{E} _{Z}$=$\frac{1}{ 2^{N-1} }$$\lbrack 3 \lbrace 2^{N}n- \frac{1}{6} \left( 5 \times 4^{ \frac{N}{2} }-2 \right) \rbrace-1 \rbrack$
整理して
$ \widetilde{E} _{Z}$$=6n-5$
(eq-5)
(eq-4)(eq-5)を用いて

$6n-5$...奇数(eq-5)
$6n-4=2(3n-2)$...偶数
$6n-3=3(2n-1)$...3の倍数
$6n-2=2(3n-1)$...偶数
$6n-1$...奇数(eq-4)
$6n=2(3n)$...偶数
従って表-1の任意の奇数列と偶数列のペアによって3の倍数を除く全ての奇数が表されている、即ち表-1には全ての奇数が存在していると云える(ag-2)

3コラッツ計算によって全ての正の整数が1に収束することの証明

3-1計算単位

A→Bの連続する操作を一つのユニットと考えることにし、その起点の数値を$u_{0}$とし、１組のユニットの一連の操作をユニット操作と呼ぶ。
Bは連続して掃除生じる場合があるが、本稿では連続回数に関わらずBは１回と数えることとする。これはA→B→B→A→B→B→B→A→B→Aという操作であったなら
A→(B)→A→(B)→A→(B)→A→(B)→Aとみなすということである。※通常のB１回分と区別するために()を付した、特に深い意味はない。
Bで辿り着く$EZ_{N}$を辿り着いた順に$EZ_{1N}$(これは$\psi$である),$EZ_{2N}$,$EZ_{3N}$,...,$EZ_{ \sigma N}$とすると、一つのユニット操作開始時が$EZ_{2N}$であったならば操作終了時は$EZ_{3N}$であることになる。即ち一つのユニット操作は$EZ_{ \sigma N}$から$EZ_{( \sigma+1 )N}$へ移動させる操作である。１回目のユニット操作後の数値を$u_{1}$,2回目のユニット操作後の数値を$u_{2}$,３回目のユニット操作後の数値を$u_{3}$,...,とする、コラッツ予想が正しいと仮定すると、何度目かのユニット操作完了後に必ず1に到達する。この時の操作回数を$p$とすると$u_{p}$=1と書ける。

3-2計算過程の一般化

$\varDelta$=2nの場合は最初の操作がBとなり、 $\psi$ に辿り着く・・・(1)
$\varDelta$=2n-1の場合は初期より$\psi$ からのスタートとなる・・・(2)
(2)は$\psi$ からのスタートと同義となる。以上より(1)(2)共に$\psi$をユニット操作の起点と考えればよい。(ag-3)
Bは何回連続で行うことになるのか予め知ることはできない、順を追った計算過程の中で初めて明らかになってゆくものである。しかしながらその操作内容は常に$\times 2^{-1} $で同じであるから１回目のユニット操作中に行われるBをまとめて$B_{u1}$,２回目のユニット操作を$B_{u2}$,３回目のユニット操作を$B_{u3}$,...と順次書くことにする。
実際に計算過程を追ってみる。

$\psi \times A \times B= u_{1}$
$u_{1} \times A \times B =u_{2} $
$u_{2} \times A \times B =u_{3} $
$u_{3} \times A \times B =u_{4} $
であるので、AとBを其々具体的な操作に戻し、u{0}からu{4}まで求めると以下のようになる。
$$ \psi...u_{0} $$
$$ \frac{3\psi+1}{ 2^{ Bu_{1} } } ...u_{1} $$
$$ \frac{9\psi+3+ 2^{ Bu_{1} } }{ 2^{ Bu_{1} } \times 2^{ Bu_{1} } } ...u_{2} $$
$$ \frac{27\psi+9+3 \times 2^{ Bu_{1} } + 2^{ Bu_{1} } \times 2^{ Bu_{2} } }{ 2^{ Bu_{1} } \times 2^{ Bu_{2} } \times 2^{ Bu_{3} }}...u_{3} $$
$$ \frac{81\psi+27+9 \times 2^{ Bu_{1} } +3 \times 2^{ Bu_{1} } \times 2^{ Bu_{2} } +2^{ Bu_{1} } \times2^{ Bu_{2} } \times 2^{ Bu_{3} } }{2^{ Bu_{1} } \times2^{ Bu_{2} } \times 2^{ Bu_{3} } \times 2^{ Bu_{4} } }...u_{4} $$
これらはユニット操作の起点$\psi$から一定の演算規則に従って行われる繰り返し操作の結果であるから、この先$u_{p}$まで同じパターンで変化してゆく、したがって一般化が可能である。以下に計算過程を一般化したものを示す。
$$ \frac{ 3^{p} \times \psi +3^{p-1}+ 3^{p-2} \times 2^{ Bu_{1}}+ 3^{p-3} \times 2^{ Bu_{1}+ Bu_{2} }+...+ 3^{p-p} \times 2^{{ Bu_{1}+...+ Bu_{p-1} } } }{ 2^{{ Bu_{1}+...+ Bu_{p-1} } } } $$
この分数式はコラッツ手順を繰り返し、次の一連のB操作を経れば1に収束するという段階におけるところまでの計算過程を示したものとなる。この段階は正に表-1における$pkZ_{0}$を示している。つまり$pkZ_{0}$と統合で結べるということであるから(eq-2)より以下のような等式で書ける。
$$ \frac{ 3^{p} \times \psi +3^{p-1}+ 3^{p-2} \times 2^{ Bu_{1}}+ 3^{p-3} \times 2^{ Bu_{1}+ Bu_{2} }+...+ 3^{p-p} \times 2^{{ Bu_{1}+...+ Bu_{p-1} } } }{ 2^{{ Bu_{1}+...+ Bu_{p-1} } } } $$
$$ = 2^{2n} $$
(eq-6)
(eq-6)について左辺の分子末項を除く全体は6の倍数になっているので変数を$h$として用いると$6h$と表わせる。分母は次数を$\tau$とすれば$2^{\tau}$と表わせる。分子末項と分母は1となるので結果として
$$ \frac{3h}{ 2^{\tau-1} }+1= 2^{2n} $$
これを変形して
$\left( 4^{n}-1 \right) 2^{\tau-1}=3h $
(eq-7)
を得る。(eq-7)の左辺は６の倍数であり、右辺は３の倍数であるから$n$,$\tau$がいかなる正の整数の組み合わせであったとしてもそれに対応する正の整数$h$は必ず存在する。
書き換えると
$$ f(n,\tau)= \frac{\left( 4^{n}-1 \right) 2^{\tau-1}}{3} $$
となる、この関数が成り立つ$n,\tau$の組み合わせは必ず存在する、即ち(eq-6)は正の整数の範囲で常に成り立っている。ただしこれが成り立つのは$n$が偶数の時のみである。このことはコラッツ手順を踏んだ場合辿り着く$pkZ_{0}$は$4^{n}$のみであるということを示している。
ここまででコラッツ計算が初期値$\Delta$がいかなる正の整数であっても最終的に1に収束することが証明できているともいえるのだが、もう少し検証してゆく。

3-3,具体例

$\psi=25$を用いる。
25-A-76-B-38-B-19
これが$ u_{1} $であり、Bは2回行われている。
-A-58-B-29
これが$ u_{2} $、Bは１回
以下同様に
-A-88-B-44-B-22-B-11
$ u_{3} $,B３回
-A-34-B-17
$ u_{4} $,B1回
-A-52-B-26-B-13
$ u_{5} $,B2回
-A40-B-20-B-10-B-5
$ u_{6} $,B3回
-A-16-B-8-B-4-B-2-B-1
$ u_{7} $,B4回
である。ここで$ u_{7} $の16が$pkZ_{0}$である。(eq-6)に当てはめると
$$ \frac{ 3^{7} \times 25+ 3^{6}+ 3^{5} \times 2^{2}+3^{4} \times 2^{3}+3^{3} \times 2^{6}+3^{2} \times 2^{7}+3^{1} \times 2^{9}+3^{0} \times 2^{12} }{ 2^{12} } $$
$$ = 4^{2} $$
最終的に$pkZ_{0}= 4^{2} $に到達してその後の一連のBによって１に収束していることが実際の順を追った計算と一致していることがわかる。

3-4,$\psi$がいかなる正の整数であってもコラッツ計算過程を経ることで1に至ることの証明

(eq-6)を$\psi$について解くことをする。
$$ \psi= \frac{1}{ 3^{p} } ( 2^{ Bu_{1}+...+ Bu_{p-1}+2n }- 3^{p-p} \times 2^{ Bu_{1}+...+ Bu_{p-1}}-...- 3^{p-3} \times 2^{ Bu^{1}+ Bu^{2} } $$
$$ - 3^{p-2} \times 2^{ Bu_{1} } - 3^{P-1} ) $$

(eq-8)
(eq-8)において括弧内の末項以外すべての項は2の倍数であるので$k$を用いて$2k$と書ける、括弧内の末項の次数は$p$の値に関わらず常に$p-1$となるから、全体として以下のように書き換えられる。
$$ \psi= \frac{2k- 3^{p-1} }{ 3^{p} } $$
(eq-9)
ここで$\psi$は整数でなければならないので、整数となる条件を考えると
$2k- 3^{p-1}= 3^{p}m $$\lbrace m \in \mathbb{Z} \vert m \gt 0 \rbrace$
よって
$2k= 3^{p}m+ 3^{p-1} $
(eq-10)
これを(eq-9)に代入して
$$ \psi= \frac{ 3^{p}m }{3^{p}} $$
この式より
$\psi=m$
(eq-11)
を得る。
次に、値$m$のとり得る範囲を調べるために(eq-10)について考える。
(eq-10)を
$2k=3^{p}m+3^{p-1}$
とし、以下のように書く
$$ f(m,p)= \frac{3^{p}m+3^{p-1}}{2} $$
この関数が整数となるには分子が偶数であればよい、分子第2項は3の累乗なので奇数である。分子第1項は３の累乗と$m$の積、$m$は正の整数なので$m$が奇数の場合、奇数✕奇数＝奇数、$m$が偶数の場合、奇数✕偶数＝偶数。分子全体として偶数になるためには第１項が奇数でなければならない,ここで奇数を$2n-1$と表わすと、結果として(eq10)は$m=2n-1$の場合常に成り立つことになる。
この結果と(eq-11)より$\psi$も同様のことがいえる、$\psi$は定義(8)より奇数でしかありえない、またユニット操作の起点は(ag-3)より$\psi$であったので全ての奇数について(eq-8)は成立すると云える。
更に(eq-8)はコラッツ手順を忠実に再現した(eq-6)を逆に辿ったものであるので、$\psi$は順序通りコラッツ手順を経ることでも$pkZ_{0}$に辿り着くと云える。このことは全ての奇数がコラッツ手順を経ることで$pkZ_{0}$に辿り着くことと同義である。そして全ての奇数が$pkZ_{0}$に辿り着くのであれば、次の一連のBによって最終的に１に到達することは自明である。更に全ての奇数が１に到達するということは自明に全ての偶数も１に到達すると云える。
以上の知見よりコラッツ手順を経ることで全ての正の整数は１に収束すると云える。

4,議論

(eq-10)は無限ループに陥ることが知られている計算手順においても成り立っている。即ち無限ループに陥る計算手順でもループに陥ることさえしなければ、基本的には1に収束する方向性であるということである。そこでループに陥ることが知られている手順と陥らないコラッツ手順の違いを明確に示す必要がある。次のセクションからはコラッツ手順がループに陥らない仕組みを紐解き、コラッツ手順がループに陥らないことを証明する。

5,コラッツ手順ではループに陥ることはないことの証明

5.1ループについて

ループはコラッツ手順のマイナスの領域で生じる他、コラッツ手順を「奇数の場合は3倍して１を引く」と書き換えた手順の場合によっても生じる。確認済みのループは1→2→1、5→14→7→20→10→5、その他$\Delta=17$とした場合に確認されているがその他でのループは確認されていない。ループには２種類あると考える一つは途中から例えば56→28→14→7→20と途中から先に挙げた5から始まるループに合流してループに陥るもの、これを開ループとすると、対してループの環から一度も外れることなく無限ループに陥る$\Delta=2,5,17$などのループを閉ループとする。ここで議論するのは閉ループについてである。
上記で閉ループを$\Delta=2,5,17$とし$\Delta=1,5,17$としなかった理由はこの後明らかになる。
奇数の時に３倍して１を引くという手順を考えてゆく、この手順をMコラッツと呼ぶことにする。以降通常のコラッツ即ち奇数の場合に３倍して１を足す手順とMコラッツを対比するために通常のコラッツ手順を単にコラッツと呼ぶこととする。
ループを考えるにあたってコラッツが閉ループを持たないことを証明するに、先ずMコラッツが閉ループを有することを論じる。
表-1において、例えばⅡ列の52項には終止$(EZ_N)$として77という数値があるのだが、これを$E77_2$と表記するのであった、ここで閉ループが確認されている数少ない数値は全て$E(2^{N}+1)_N$と表記できる。具体的には$E2_0=2^{0}+1$,$E5_2=2^{2}+1$,$E7_4=2^{4}+1$である。
では$\psi=17$の場合の計算過程を順を追ってみてみる
17→50→25→74→37→110→55→164→82→41→122→61→182→91→272→136→68→34→17
最後のB操作に着目すると272→136→68→34→17であり、これは$E17_4$即ちⅣ列目に存在する17以外に考えられない計算過程である。
同様に$\psi=5$の場合も確認する
5→14→7→20→10→5、最後のB操作に着目すると20→10→5でありこれは$E5_2$即ちⅡ列目に存在する5以外には考えられない計算過程となっている。
更に$\psi=2$の場合、1→2→1B操作は2→1であり、これは$E2_0$即ち０列目に存在する2の計算過程以外は考えられない。
先ほど閉ループの生じる初期値を１でなく２としたのはこのことに由来する。
※これは$n^{0}=1$と定められているように整合性をとったものである。以下にMコラッツの表を提示する。

5.2Mコラッツ表

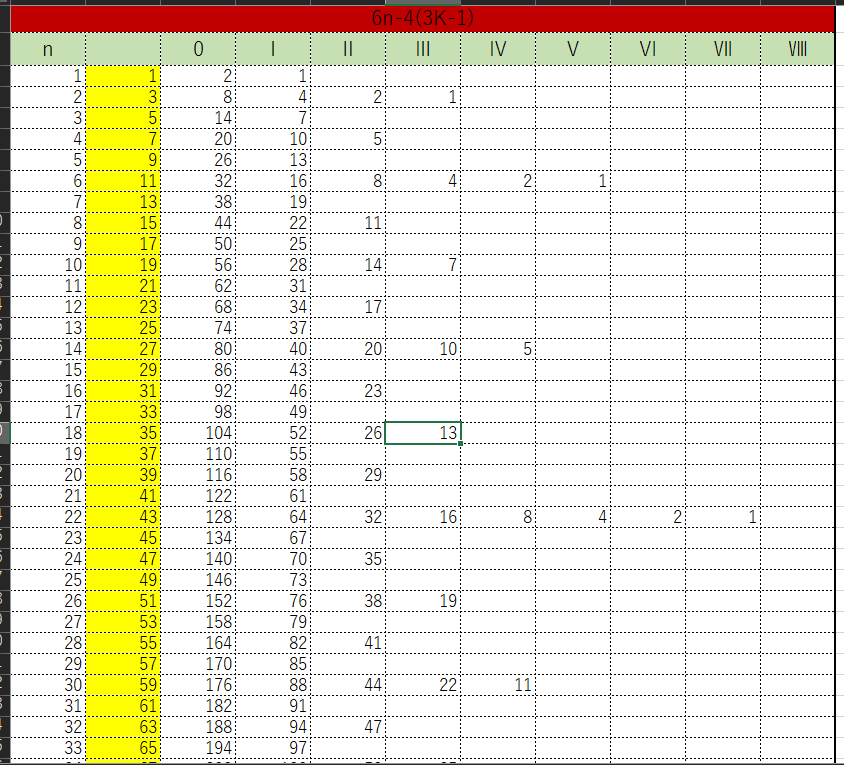Mコラッツ
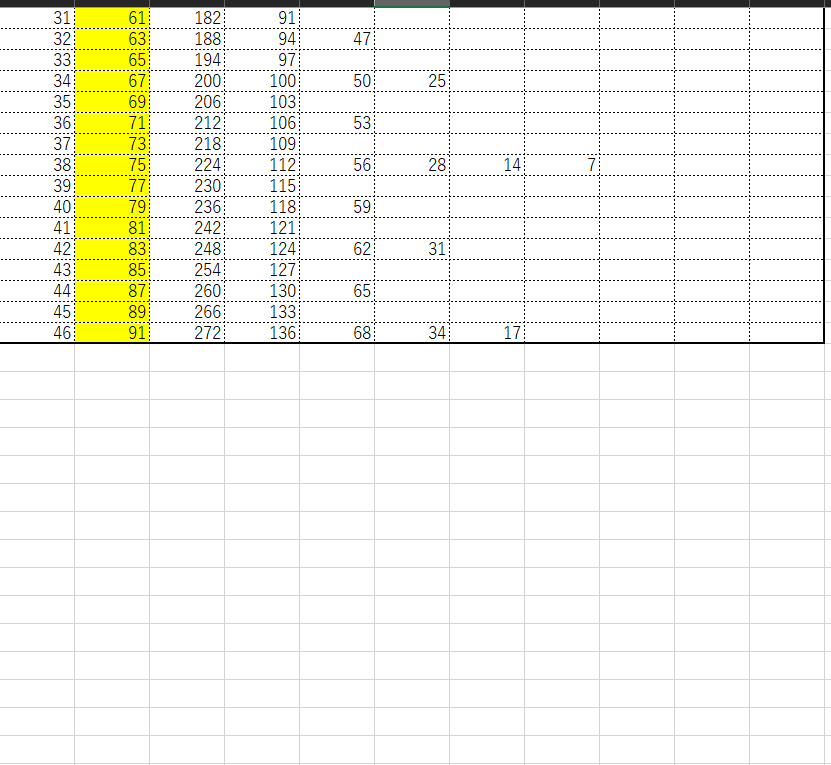Mコラッツ続き
Mコラッツ表中の定義は先に示したコラッツ表の定義とほぼ同じであるが、異なる点だけを示しておく。
$Z_0=6n-4$
(eq-12)
$$ Z_N= \frac{3n-2}{2^{N-1}} $$
(eq-13)

5.3Mコラッツで閉ループが生じるシステム

先ずは(eq-6)の左辺をMコラッツに書き換える
$$ \frac{ 3^{p} \times \psi -3^{p-1}- 3^{p-2} \times 2^{ Bu_{1}}- 3^{p-3} \times 2^{ Bu_{1}- Bu_{2} }-...- 3^{p-p} \times 2^{{ Bu_{1}+...+ Bu_{p-1} } } }{ 2^{{ Bu_{1}+...+ Bu_{p-1} } } } $$
(fo-1)
(fo-1)の分母は$2^{ Bu_{1}+...+ Bu_{p-1} } $即ち$Bu_{p-1}$までなので$Z_0$の値を返している。仮にここが$EZ_N$であれば続けて最後のB操作を行うことによって$EZ_N$に至るので、返される値は$EZ_N$である
$Z_0$は任意の$EZ_N$に対してBを行う前の状態といえるから$2^{N}EZ_N$といえる。例えば$\Delta=17$の場合17→50→25→74→37→110→55→164→82→41→122→61→182→91→272→136→68→34→17という経路をたどるのでループ完成の17に至る前の、つまり272→136→68→34→17というBを行う前の状態は$Z_0=272$であるが、ここまでの計算は$Bu_{p-1}$としたときであり、$EZ_N=17$でループ完成した時まで計算するときは$EZ_N$までの計算となるということである。そして$E17_4$は272でありこれは$2^{4} \times 17$である。
このことはセクション3.3で行った具体例を参照してほしい。またMコラッツの数値の動き方についてはセクション5.2のMコラッツ表を参照してほしい。以上のことから$\psi=(2^{N}+1)$とし、(fo-1)の対辺を$2^{N}(2^{N}+1)$とすると
$$ \frac{ 3^{p} \times (2^{N}+1) -3^{p-1}- 3^{p-2} \times 2^{ Bu_{1}}- 3^{p-3} \times 2^{ Bu_{1}- Bu_{2} }-... }{ 2^{{ Bu_{1}+...+ Bu_{p-1} } } } $$
$$ \frac{- 3^{p-p} \times 2^{{ Bu_{1}+...+ Bu_{p-1} } }}{{ 2^{{ Bu_{1}+...+ Bu_{p-1} } } }}=2^{N}(2^{N}+1)$$
(eq-14)
を得る。
【※右辺を奇数全般として与えれば話は早いのですが（もちろん後程奇数全般についても考えます）、具体的な数値を当てはめることでMコラッツがループする要件をいかに満たし、コラッツがループ要件をいかに回避しているかのシステムを語ることができるようになるため、先ずこのような形をとっています】
(eq-14)の分子については末項を除いて6の倍数であるので$6k$と書く末項は分母と同じであるので1となる。結果として以下のように書ける。
$$ \frac{3h}{2^{\tau-1}}-1=2^{N}(2^{N}+1) \lbrace h,\tau \in + \mathbb{N} \rbrace $$
(eq-15)
(eq-15)の右辺は先にも述べたように$Z_0 $である、コラッツでは$Z_0=6n-2$であり、Mコラッツでは$Z_0=6n-4$なのでどちらも偶数である。従って整数の範囲において左辺が偶数になる条件は以下のようになる。
$$ \tau-(1+\delta) \lt 0 \Longleftrightarrow h=2n $$
(ag-4)
次に(eq-15)を$h$について解くと
$$ h= \frac{2^{\tau-1}}{3}(2^{N}+4^{N}+1) $$
この式は$N=2n$即ち偶数列の場合に必ず整数となり(ag-4)を満たす。(ag-5)
$N=2n-1$即ち奇数列の場合には必ず整数値にならない。(ag-6)
次に(eq-15)の右辺が$2^{N}(2^{N}-1)$の場合を考える。同様に$h$について解いて
$$ h= \frac{2^{\tau-1}}{3}(-2^{N}+4^{N}+1) $$
この式は$N=2n-1$即ち奇数列の場合に整数となり(ag-4)を満たす。(ag-7)
他方偶数列の時には整数値とならない。(ag-8)
次に(eq-15)の右辺が奇数全般である場合を考える。
コラッツにおける各列の一般項(eq-1)を用いる。(eq-1)が表すのは$EZ_N$であるので、これに$2^{N}$を掛けたものは$Z_0$となる。
$$ \frac{3h}{2^{\tau-1}}-1= \frac{2^{N}(3n-1)}{2^{N-1}} $$
(eq-16)
$h$について解くと
$$ h= \frac{1}{3}(6n-1)2^{\tau-1} $$
(eq-16)で$h$は整数にならない。
一方Mコラッツでは
$$ \frac{3h}{2^{\tau-1}}-1= \frac{2^{N}(3n-2)}{2^{N-1}} $$
$h$について解いて
$$ h= \frac{1}{3}(6n-1)2^{\tau-1} $$