コラッツ予想の証明において、示した一般項の数列にすべての自然数が存在すればパスが一通りになるのか②

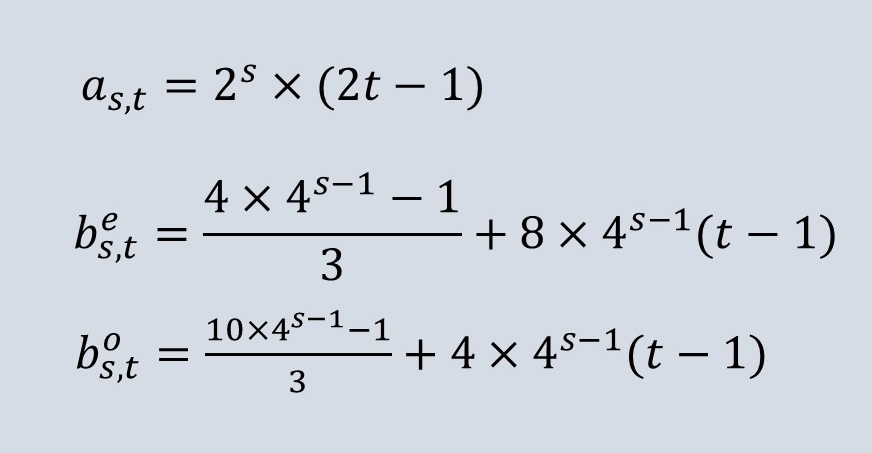
３つの式で、すべての正の整数を表わせることを述べてきました。
すべて表すことができれば、コラッツ予想は真である、ということが理解していただけるように、あともう一言、解説してみたいと思います。

bの２式で奇数すべてを表せ、6t-1と6t-5で次に連結する奇数を示せます。それぞれで、奇数は一度しか存在しないので、数が重複することによるループはないわけです。
これらを図に配置するとしたらこの図からもれる奇数はありません。

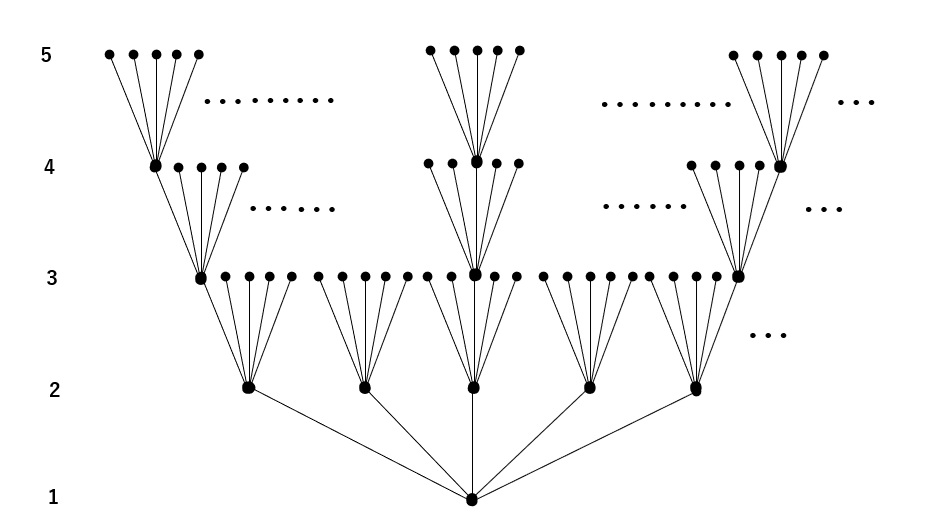
コラッツの計算を行うとき、最初の数をまず決めます。最初の奇数が決まってきます。
決めた時点で、図2のように計算過程を考えると、この図のどこか一点がスタート地点となります。
そこからは、奇数になるまで2で割る回数が偶数のときは6t-5、奇数のときは6t-1で次の奇数が参照できるわけです。
最初の奇数は、その奇数により、ただ一つ、高さ（1になるまでに通る奇数の数）が決まってきます。参照する毎にその高さは一つずつ減っていきます。

だから、必ず1に到達します。

27のように、いつまでも1に到達しないかのように計算値自体は増えていくことがあろうとも、このツリー図においては、確実に一つずつ降りてきているわけです。

イメージしていただけたら、うれしいです😊
読んでいただいて、ありがとうございました！