算術三角形の基本

算術三角形のつくり方

算術三角形とは、下図のような三角形のことである。以下、一番上の段を0段目、その下の段を1段目、さらにその下の段を2段目、と呼ぶことにする。

この三角形は、隣り合う数字を足した数が、真下に来るように作られている。ただし、端の数はすべて1である。例えば、5段目は左から端を除いて$1+4=5$,$4+6=10$,$6+4=10$,$4+1=5$となっている。
算術三角形

この三角形は普通パスカルの三角形と呼ばれるが、僕はカタカナより漢字が好きなので、算術三角形と呼んでいる。算術とは足し算のことで算術平均や算術級数といった言葉がある。この三角形は足し算によって作られるから、算術三角形と呼ぶ。

算術三角形には面白い性質がたくさんある。

一番端の列はすべて1である。1つ内側を見れば、自然数が小さい順に並んでいる。その内側は三角数と呼ばれるもので、正三角形の形に点を並べた時の点の総数である。また、1からある数までの和でもなる。その内側は四面体数と呼ばれる数が並ぶ。これもやはり四面体の形に端を並べた時の点の総数である。次の列は五胞体数が並ぶ。五胞体とは四次元図形の一種で、いうなれば四次元版三角形(四次元版四面体でもいい)である。

斜めに並んでいる数をたしてゆけば、その答えは最後の数の斜め下に現れることがわかる。例えば、下に太字で表した部分は$1+3+6+10=20$となっている。そのすぐ右下を見れば$1+4+10+20=35$である。確かめてみれば、ほかの部分でもそのようになることがわかる。
斜めの和

組み合わせ

例えば、青、赤、黄、白、黒の5色から2色選ぶ方法は

• 青赤
• 青黄
• 青白
• 青黒
• 赤黄
• 赤白
• 赤黒
• 黄白
• 黄黒
• 白黒

の10通りで、${}_5C_2=\frac{5!}{2!3!}=10$である。

実は、算術三角形の各項はこの組み合わせの数に等しい。例えば、6段目は1, 6, 15, 20, 15, 6, 1となっていて、$\combi{6}{0}=1$, $\combi{6}{1}=6$, $\combi{6}{2}=15$, $\combi{6}{3}=20$, $\combi{6}{4}=15$, $\combi{6}{5}=6$, $\combi{6}{6}=1$である。

$ \begin{align*} \combi{n}{r+1}+\combi{n}{r}&=\frac{n!}{(r+1)!(n-r-1)!}+\frac{n!}{r!(n-r)!}\\ &=\frac{n!(n-r)}{(r+1)!(n-r)!}+\frac{n!(r+1)}{(r+1)!(n-r)!}\\ &=\frac{(n+1)!}{(r+1)!(n-r)!}=\combi{n+1}{r+1} \end{align*} $

組み合わせの数のこの性質と算術三角形の作り方はきれいに一致し、端の数がすべて1であることから、両者が等しくなることがわかるであろう。

したがって算術三角形は下図のようにも書ける。
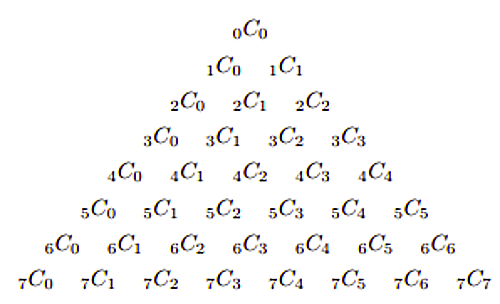組合せ三角形