算術三角形からフィボナッチ数列を作る
算術三角形からフィボナッチ数列を作る
算術三角形は普通下図のように描かれる。
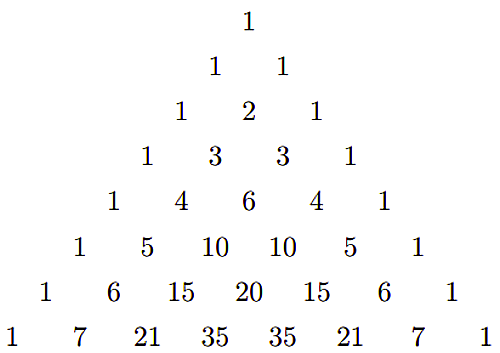 算術三角形
算術三角形
これからフィボナッチ数列を作るには、以下のように斜めにし、縦に並んだところで足すとわかりやすい。
 算術三角形とフィボナッチ数列
算術三角形とフィボナッチ数列
証明するには、算術三角形を組合せの数で見てあげると良い。
フィボナッチ数列$(F_n)$は組合せの数$\combi{n}{r}$により以下のように表せる。ただし$[x]$は$x$以下の最大の整数を表す。$$ F_n=\sum_{r=0}^{[\frac{n-1}{2}]}\combi{n-r-1}{r} $$
$\sum_{r=0}^{[\frac{n-1}{2}]}\combi{n-r-1}{r}$がフィボナッチ数列の漸化式を満たせばよい。
$F_1,\ F_2$について
$
\begin{align*}
\sum_{r=0}^{[\frac{1-1}{2}]}\combi{1-r-1}{r}=\combi{0}{0}=1\\
\sum_{r=0}^{[\frac{2-1}{2}]}\combi{2-r-1}{r}=\combi{1}{0}=1\\
\end{align*}$
$n$が偶数のとき$n=2m$なる整数$m$が在って
$
\begin{align*}
\sum_{r=0}^{[\frac{n-1}{2}]}\combi{n-r-1}{r}+\sum_{r=0}^{[\frac{n}{2}]}\combi{n-r}{r}&=\sum_{r=0}^{m-1}\combi{2m-r-1}{r}+\sum_{r=0}^{m}\combi{2m-r}{r}\\
&=\sum_{r=1}^{m}\combi{2m-r}{r-1}+\sum_{r=1}^{m}\combi{2m-r}{r}+\combi{2m}{0}\\
&=\sum_{r=1}^{m}\left(\combi{2m-r}{r-1}+\combi{2m-r}{r} \right)+\combi{2m+1}{0}\\
&=\sum_{r=0}^{m}\combi{2m-r+1}{r}=\sum_{r=0}^{[\frac{n+1}{2}]}\combi{n-r+1}{r}
\end{align*}
$
$n$が奇数のとき$n=2m+1$なる整数$m$が在って
$
\begin{align*}
\sum_{r=0}^{[\frac{n-1}{2}]}\combi{n-r-1}{r}+\sum_{r=0}^{[\frac{n}{2}]}\combi{n-r}{r}&=\sum_{r=0}^{m}\combi{2m-r}{r}+\sum_{r=0}^{m}\combi{2m-r+1}{r}\\
&=\combi{m}{m}+\sum_{r=0}^{m-1}\combi{2m-r}{r}+\sum_{r=1}^{m}\combi{2m-r+1}{r}+\combi{2m-1}{0}\\
&=\combi{m+1}{m+1}+\sum_{r=1}^{m}\combi{2m-r+1}{r-1}+\sum_{r=1}^{m}\combi{2m-r+1}{r}+\combi{2m}{0}\\
&=\sum_{r=0}^{m+1}\combi{2m-r+2}{r}=\sum_{r=0}^{[\frac{n+1}{2}]}\combi{n-r+1}{r}
\end{align*}
$
以上より$\sum_{r=0}^{[\frac{n-1}{2}]}\combi{n-r-1}{r}$はフィボナッチ数列の漸化式を満たす。
この証明では任意の非負整数$n$について$\combi{n}{0}=\combi{n}{n}=1$であることを利用している。また組み合わせの数の公式$\combi{n+1}{r+1}=\combi{n}{r+1}+\combi{n}{r}$を使っている。
