すべての放物線は相似

意外と知られていないようですが, すべての放物線は相似です.
証明します.
2 つの放物線 C1:$y=ax^2$, C2:$y=bx^2$ ($0< b< a$) が相似であることをみれば十分です.

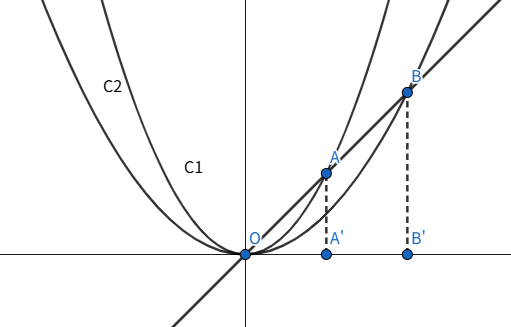
原点が相似の中心であることを確認します.
$c \neq 0$ について,
直線 $y=cx$ と放物線 C1 との交点のうち, 原点でない方を A,
直線 $y=cx$ と放物線 C2 との交点のうち, 原点でない方を B とします.
A の $x$ 座標は $ax^2=cx$ を解いて $\frac{c}{a}$,
B の $x$ 座標は $bx^2=cx$ を解いて $\frac{c}{b}$.
したがって,
A から $x$ 軸に下ろした垂線の足は A'$(\frac{c}{a},0)$,
B から $x$ 軸に下ろした垂線の足は B'$(\frac{c}{b},0)$.
よって,
OA:OB$=$OA':OB'$=\frac{c}{a}:\frac{c}{b}=\frac{1}{a}:\frac{1}{b}$
これは $c$ の値によらないので, 放物線 C1 と放物線 C2 は相似で, 相似比は $\frac{1}{a}:\frac{1}{b}$ です.