初等的な単振り子のθについての微分方程式導出

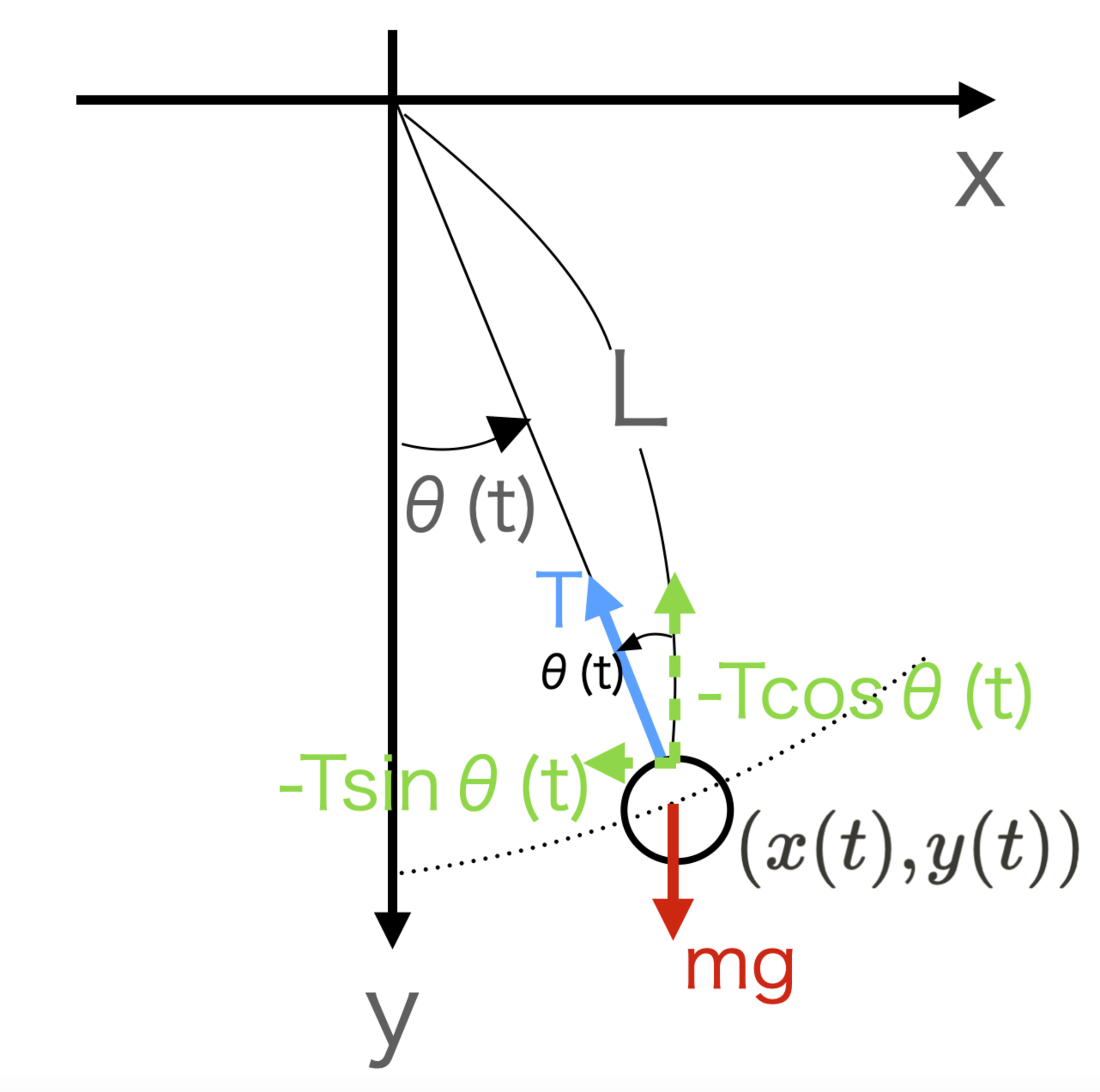単振り子

proof:
図より、
$\displaystyle x(t)= Lsin\theta(t),\ $$\displaystyle y(t)= Lcos\theta(t)$である。

各々について合成関数の微分をすると、
$\displaystyle v_x(t)= L\frac{d\theta}{dt}(t)cos\theta(t)$,　$\displaystyle v_y(t)= -L\frac{d\theta}{dt}(t)sin\theta(t)$

さらに各々を微分すると、
$\displaystyle a_x(t)= L\big(\frac{d^2\theta}{dt^2}(t)cos\theta(t)- \big(\frac{d\theta}{dt}(t)\big)^2sin\theta(t) \big)$

$\displaystyle a_y(t)= -L\big( \frac{d^2\theta}{dt^2}(t)sin\theta(t)+\big(\frac{d\theta}{dt}(t)\big)^2cos\theta(t)\big)$である。

又、$\displaystyle F_x=-Tsin\theta (t)$,$F_y=mg-Tcos\theta (t)$より、運動方程式を立てる。

$\displaystyle ma_x(t)= F_x$より、
$\displaystyle mL\Big(\frac{d^2\theta}{dt^2}(t)cos\theta(t)- \Big(\frac{d\theta}{dt}(t)\Big)^2sin\theta(t) \Big)= -Tsin\theta (t) \ \ \cdots(1)$

$\displaystyle ma_y(t)= F_y$より、
$\displaystyle -mL\Big(\frac{d^2\theta}{dt^2}(t)sin\theta(t)+\Big(\frac{d\theta}{dt}(t)\Big)^2sin\theta(t)\Big)= mg-Tcos\theta (t)\ \ \cdots(2)$

[(1)式]$\times \cos\theta(t) - [(2)式]\times \sin \theta(t)$をして、$\sin^2 \theta(t)+\cos^2 \theta(t)=1$を用いて計算を行うと、
$\displaystyle mL\frac{d^2\theta}{dt^2}(t) = - mg\sin\theta(t)$
$\Leftrightarrow \displaystyle \frac{d^2\theta}{dt^2}(t) = - \frac{g}{L}\sin\theta(t)$

ここで、$\theta(t)$が任意の時刻で小さい時に、$ \displaystyle \sin \theta (t)を\theta(t)$で近似すると、$\displaystyle \frac{d^2\theta}{dt^2}(t) = - \frac{g}{L}\theta(t) $となる。

これは単振動型の微分方程式であるので、
$\displaystyle \omega=\sqrt{\frac{g}{L}}\ \ \ [rad/秒] \ \ ,\ \ T=2\pi\sqrt{\frac{L}{g}} \ \ \ [秒]$となる。
Q.E.D