東大寺学園数学研究部　懸賞問題解説　その2　問13,15,17

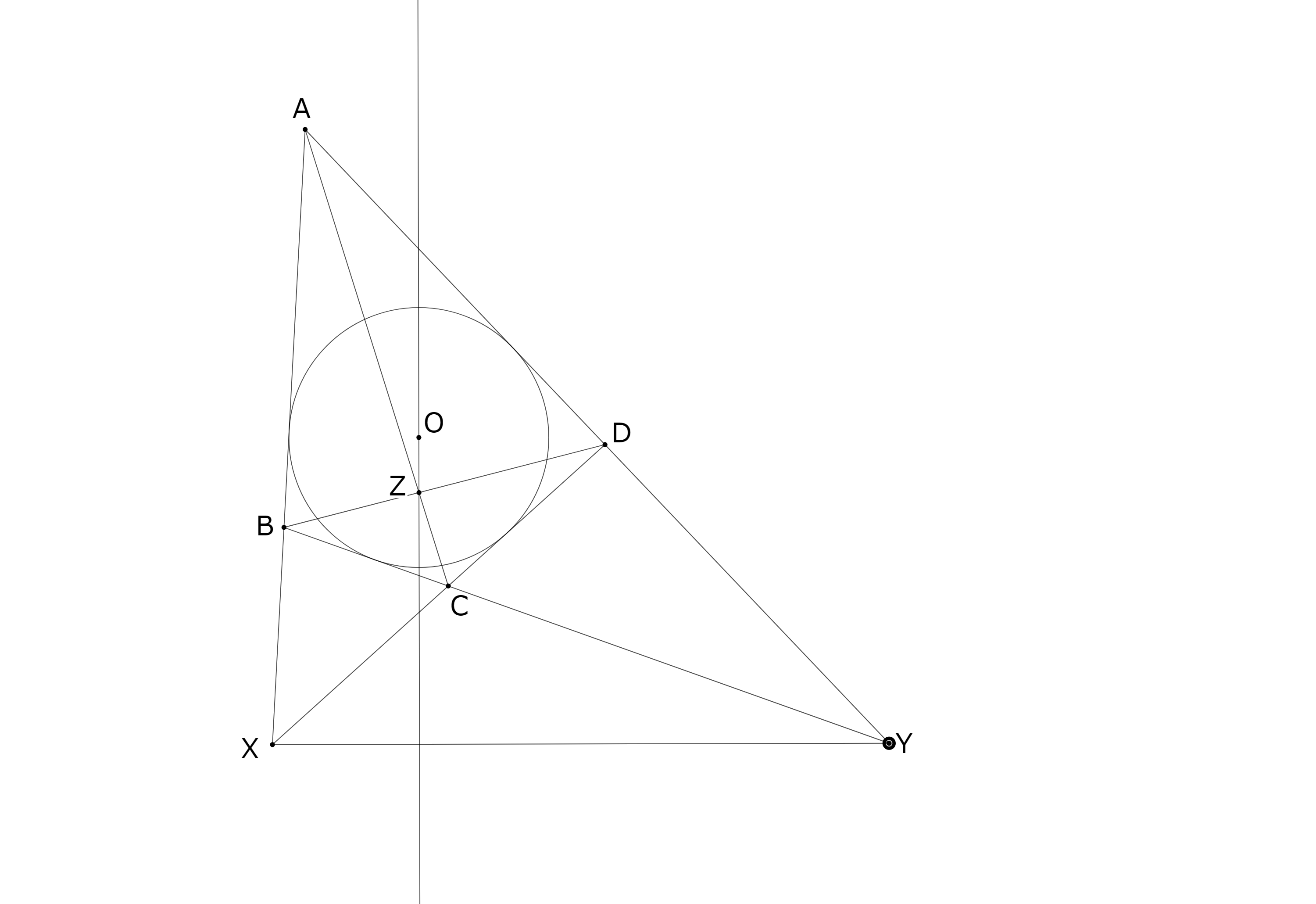
$O$を中心とし,四角形$ABCD$に内接する円を$\omega$とする.
直線$AB,BC,CD,DA$と$\omega$の接点をそれぞれ$P,Q,R,S$とする.$\angle XPO=\angle XRO=90°$より,四角形$XPOR$は円に内接する.この円を$\Gamma_{1}$とする.$\Gamma_{1}$と直線$XY$の交点を$H(\neq X)$とすれば,$\angle YQO=\angle YSO=\angle YHO=90°$なので,四角形$YQOS$は円に内接し,かつ,この円を$\Gamma_{2}$とすれば,$\Gamma_{2}$は$H$を通る.
さて,$PR$と$QS$の交点を$Z'$とすれば,$Z'$は$\omega ,\Gamma_{1},\Gamma_{2}$の根心なので,$OH$は$Z'$を通る.よって,$XY\perp OZ'$である.そこで,$Z'=Z$であることを示せばよいが,これはブリアンションの定理を六点$A,P,B,C,R,D$,六点$A,B,Q,C,D,S$にそれぞれ適用することで得られる.

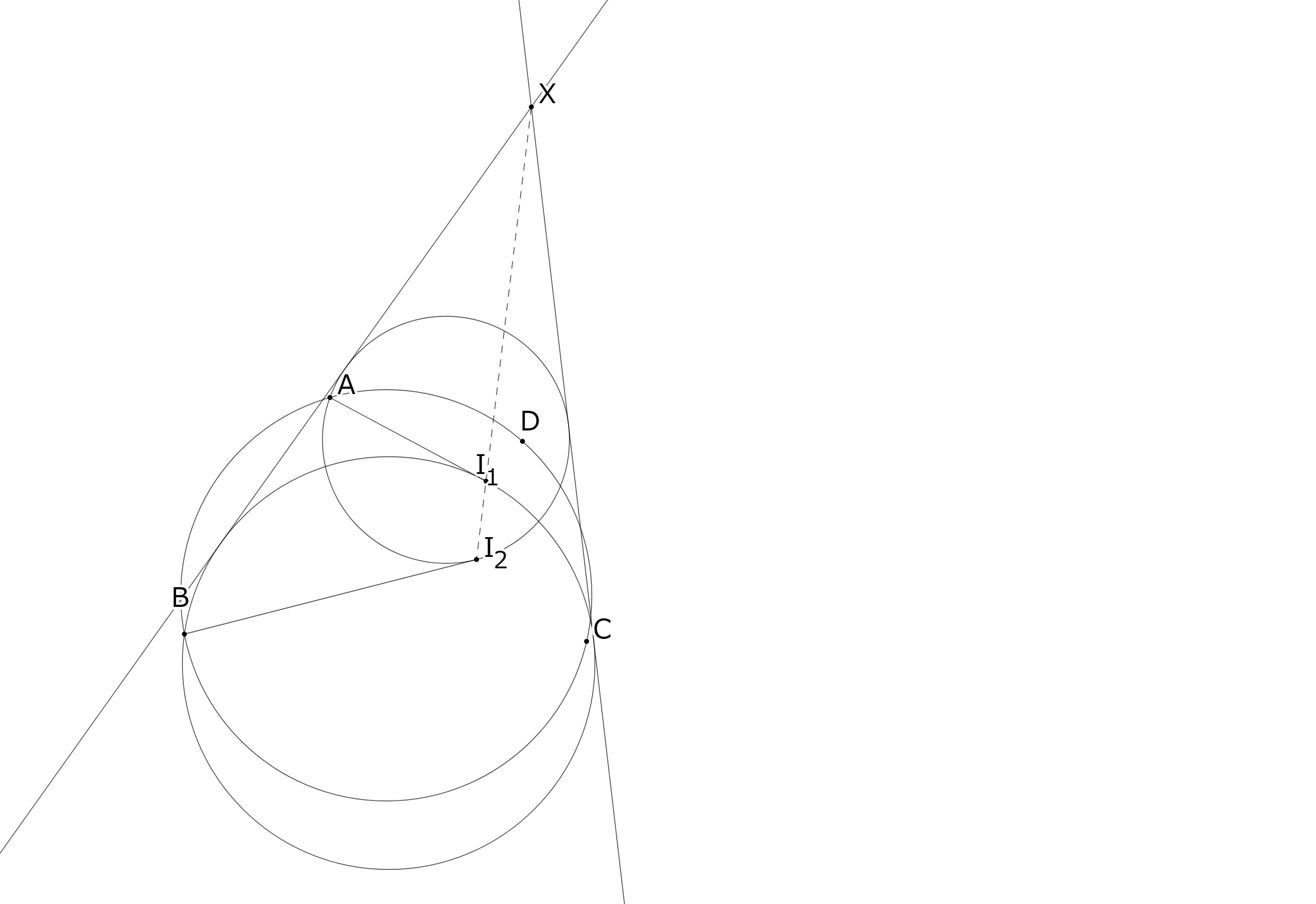
二点$A,I_2$を通り直線$BI_2$に接する円を$\omega_1$,二点$B,I_1$を通り直線$AI_1$に接する円を$\omega_2$とする.
弧$CD$のうち点$A$を含まない方の中点を$M$とする.明らかに三点$A,I_{1},M$,三点$B,I_{2},M$はそれぞれ一直線上にある.また,
$\angle MI_{1}D=\angle I_{1}AD+\angle I_{1}DA=\angle I_{1}AC+\angle I_{1}DC=\angle MDC+\angle I_{1}DC=\angle MDI_{1}$
より$MI_{1}=MD$.同様にすれば$MI_{2}=MC$.さらに,明らかに$MD=MC$であるから$MI_{1}=MI_{2}$.
よって,直線$MI_{1},MI_{2}$にそれぞれ点$I_{1},I_{2}$で接する円をとることができる.すると,この円と$\omega_1$と$\omega_2$に$monge$の定理を適用することで,三点$X,I_{1},I_{2}$が一直線上にあることが得られる.

三角形$ABC$の接触三角形を$PQR$とする.
$\angle C$の外角の二等分線と$AB$の交点を$F$とする.角の二等分線の性質とメネラウスの定理の逆から,三点$D,E,F$が一直線上にあることがわかる.また,角度計算により四角形$ADPI$が円に内接することが分かる.この円を$\Gamma_{A}$とおく.同様にして$\Gamma_{B},\Gamma_{C}$を定める.$\Gamma_{A}$と$DE$交点を$H$とすれば,$\angle DHI=90°$より,$\Gamma_{B},\Gamma_{C}$も$H$を通る.
ここで,三角形$ABC$の内接円について反転する.
$\Omega$が反転して移った先を$\Omega'$と表すこととする.
$A',B',C'$はそれぞれ$QR,RP,PQ$の中点である.よって,$H'$は三角形$PQR$の重心である.さて,三点$H,H',I$は一直線上にあるので,示したいことは三点$H',I,O$が一直線上にあることである.ここで,$I$は三角形$PQR$の外心であることに注意すれば,三角形$PQR$のオイラー線上に三角形$ABC$の外心があることを示せばよい.そこで,三角形$PQR$の垂心を$K$,九点円の中心を$L$とする.
$PK$と$QR$の交点を$S$,$QK$と$RP$の交点を$T$,$RK$と$PQ$の交点を$R$とする.
角度計算により,$ST\parallel AB$が分かる.同様に,$TR\parallel BC$,$RS\parallel CA$である.すると,三角形$ABC$と三角形$STU$の相似の中心$X$をとることができる.角度計算により,$K$は三角形$STU$の内心であることがわかるので,$X$を中心とした相似拡大を考えることにより,三点$X,K,I$が一直線上にあることがわかる.すなわち,$X$は三角形$PQR$のオイラー線上にある.また,$L$は三角形$STU$の外心であるから,再度$X$を中心とした相似拡大を考えることにより,三点$X,L,O$が一直線上にあることがわかる.よって,三角形$PQR$のオイラー線上に$O$があることが示された.

$\Gamma_{B},\Gamma_{C}$が$H$を通ることを示すまでは同様.
$\Gamma_{A}$と円$ABC$の交点を$S(\neq A)$とする.同様にして,$T,U$を定める.角度計算により,四角形$PQTS$が円に内接することがわかる.同様にすれば,四角形$QRUT$,四角形$RPSU$はそれぞれ円に内接する.円$PQTS$,円$QRUT$,円$RPSU$,$\Gamma_{A}$,$\Gamma_{B}$,$\Gamma_{C}$の六円のうち任意の二円の根軸は一点で交わるので,この点を$X$とする.$X$を中心とする,半径$\sqrt{XI\times XH}$の反転によって,点$P,Q,R$はそれぞれ点$S,T,U$にうつる.すなわち,この反転によって,三角形$ABC$の内接円と外接円は互いに移りあう.よって,三点$I,X,O$は一直線上にある.これと三点$H,I,X$が一直線上にあることをあわせて,三点$H,I,O$が一直線上にあることがわかる.よって,$OI\perp DE$である.

三角形$ABC$の傍心を$I_{A},I_{B},I_{C}$とおく.$I$,は三角形$I_{A}I_{B}I_{C}$の垂心,$O$は三角形$I_{A}I_{B}I_{C}$の九点円の中心なので,直線$OI$は三角形$I_{A}I_{B}I_{C}$のオイラー線である.よって,三角形$I_{A}I_{B}I_{C}$の外心を$O'$とすれば,$OO'\perp DE$であることを示せばよい.そこで,円$ABC$,円$I_{A}I_{B}I_{C}$の根軸$l$が$DE$と一致することを示す.
四角形$BCI_{B}I_{C}$は円に内接するので,$DI_{C}\times DI_{B}=DB\times DC$,すなわち,$D$における円$ABC$と円$I_{A}I_{B}I_{C}$への方べきが一致するので,$D$は直線$l$上にある.同様にすれば,$E$が直線$l$上にあることが示されるので,$DE=l$.よって示された.