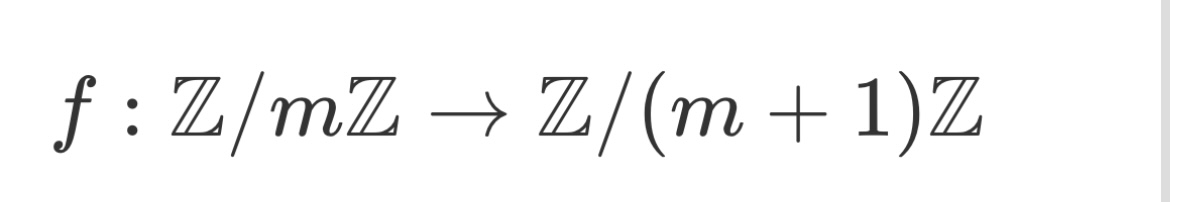未解決問題ノート
この記事について
この記事は自分が作った問題の中で、未だに解けていないものをのせています
進捗なども記録します。
良い解法等あったら教えてくださると嬉しいです。
本編
自然数の組$(a,b,c)$に対して$2^a+2^b+2^c$が平方数となるものを求めよ。
追記
ご指摘のあった通り$c=1,k=2$とすると
$(a,b)=(0,0)$なので、求めるものを自然数の組$(a,b,c)$から非負整数の組$(a,b,c)$とします。
進捗
$2^a+2^b+2^c=k^2(k \in \mathbb{N})$としてみる。
まあどうせ左辺は偶数なので右辺も偶数だね。つまり$k$は偶数。
例えば$c=1,k=2$としてみる。
$2^a+2^b=2$.これを満たす自然数の組は
$(a,b)=(0,0)$.
最近対称性というものを知ったので、
$a\geq b \geq c$としましょう。
多分$a\gt b\gt c$としてしまうと、さっきの例は成り立たなくなってしまい不都合な気がします。
問題1のもしかして
もしかして:頑張ったら因数分解できる(整数範囲)
もしかして2:$2^a+2^b+2^c=2^c(2^{a-c}+2^{b-c}+1)$とするとうまくいく
もしかして:$\mod{}$を使う
ちなみに、これの問題を一般化した問題もあります
$k \in \mathbb{N}$に対して$k^a+k^b+k^c$が
成り立つような非負整数の組$(a,b,c)$
を求めよ。
...無理ゲーぽそうですね
$f:G_1 \to G_2 ;\text{homomorphism}$
このとき、$\phi:\mbox{ker}(f)\to \mbox{Im}(f)$はどのような性質を持つか?
また$f$が$\mbox{isomorphism}$のときや、$\mbox{endomorphism},\mbox{automorphism}$のときは、どのような性質を持つか?
進捗
JJMOが終わって、受験勉強の合間にやろうと思います。
進捗がないので妄想
もしかして:全射とか単射とか準同型
もしかして2:同型(という感じではない)
もしかして3:$\mbox{Im}(\phi)$とかはベクトル空間になる
ネガティブなもしかして4:そもそも$\phi$は
面白そうな性質を持たない
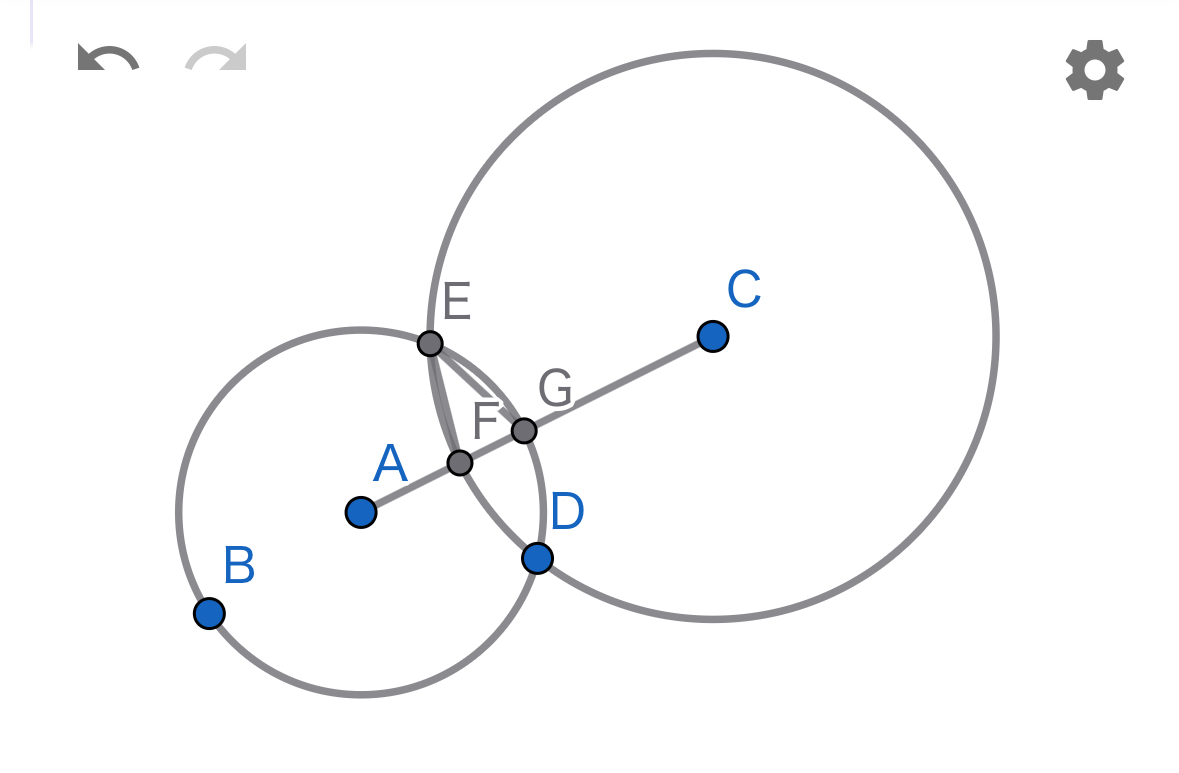 問題の図
問題の図
点$A,C$を中心とする円$S_1,S_2$とし、
線分$AC$と円$S_1,S_2$の交点をそれぞれ
$F,G$、$S_1,S_2$の交点を$E$とする。
この時$\triangle EFG$が
(1)二等辺三角形
(2)直角三角形
(3)正三角形
(4)その他のなにか
になるためにはどのような条件が必要か?
進捗
全くもってなし
幾何の典型的な考察わからないのまずいですね
もしかして...?
・座標平面上で考える
・円の弦の長さに関して何か有用な定理などがある...?
・ナーマギリ女神が教えてくださる