円に内接するn角形で面積最大のもの

はじめに

表題の件について、高校生が初等的な証明をしたらしいのでメモ。
youtubeの解説動画は見たけど論文の原文は未読です。
論文では面積を最大化するアルゴリズムについて丁寧に検討しているみたいですが、
なんか難しそうだったのでそこは省略します。
それでも証明としては成立する気がするので記事にしてみました。
ダメっぽかったらご指摘いただけると幸いです。

準備

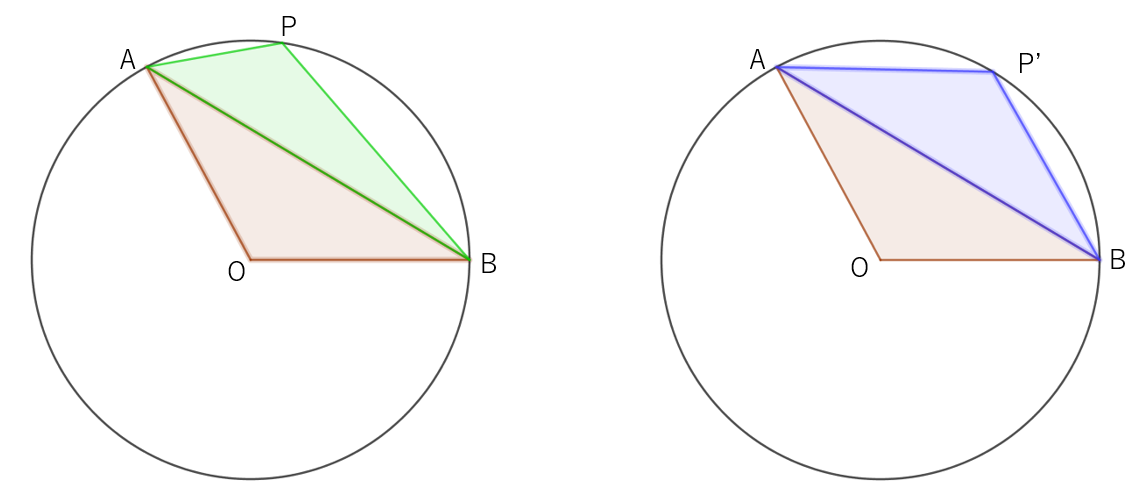
図1のような四角形OAPBについて考える。
点Pが弧AB上を動くとすると、四角形の面積が最大となるのは点Pが弧ABの中心にくるとき。
言いかえると、弦APと弦BPの中心角が等しくなるときである（図2）。

本論

円に内接する$n$角形において、隣接する2辺と円の中心Oからなる四角形に対して先の議論を適用できる。
すると、2辺のそれぞれの中心角が異なる場合にはそれを平均化することで、その部分の面積が増加することが分かる。

それを念頭に、円に内接する$n$角形のうち最大の面積を持つものについて考える。

ある内接$n$角形について、隣接する辺のペアをみたときに中心角が異なっていたとする。
そのとき、その中心角を平均化することで$n$角形の面積を増やせるので、その$n$角形は面積最大とは言えない。

よって求める$n$角形は「どの隣接ペアをみても中心角が等しい」必要がある。
その場合「すべての辺の中心角が等しい」と言えるので、それは正$n$角形である。

おわりに

高校生すげえ