Crazy Ant Problem
Crazy Ant Problem とは
Crazy Ant Problem とは座標平面の原点にいるアリがx軸方向に1進んで反時計回りに60度回転し、次に$\frac{1}{2}$進んで同じだけ回転し、同様に$\frac{1}{3}$進んで回転、$\frac{1}{4}$進んで回転……と無限に続けたときのゴールの座標を求める問題です。
 CrazyAnt
CrazyAnt
複素数平面と、複素数版の対数関数のマクローリン展開(下記)を使うことでこの問題を解くことができます。しかも、回転角度が何度であっても計算できます。以下では回転角度を $\theta$ としてゴールの座標を求めます。複素数の対数関数は多価関数になりますが、ここでは主値のみを考えればよいので以下では主値を用います。
${\displaystyle -\log(1-x)=\sum_{n=1}^{\infty}\frac{x^n}{n} }$
複素数平面上で考えた場合のアリのゴールの位置を $P$ とすると、$(P\in\mathbb{C})$
${\displaystyle
\begin{align}
P&=\sum_{n=1}^{\infty}
\frac{e^{i(n-1)\theta}}{n}\\
&=e^{-i\theta}\sum_{n=1}^{\infty}
\frac{e^{in\theta}}{n}\\
&=-e^{-i\theta}\log\left(
1-e^{i\theta}
\right)\\
&=-e^{-i\theta}\left(
\log\left|1-e^{i\theta}\right|
+i\arg \left(1-e^{i\theta}\right)
\right)\\
&=-(\cos \theta-i\sin \theta)
\left(
\log2+\log\left|\sin\frac{\theta}{2}\right|
+i\left(\frac{\theta-\pi}{2}\right)
\right)\\
&=\left(\frac{\pi-\theta}{2}\sin\theta-\cos \theta
\left(
\log2+\log\left|\sin\frac{\theta}{2}\right|\right)
\right)
+i\left(
\left(\log2+\log\left|\sin\frac{\theta}{2}\right|\right)\sin \theta
+\frac{\pi-\theta}{2}
\cos \theta\right)\\
\end{align}
}$
したがって、x,y座標平面上で表すとアリのゴールは
${\displaystyle
\left(\left(\frac{\pi-\theta}{2}\sin\theta-\cos \theta
\left(
\log2+\log\left|\sin\frac{\theta}{2}\right|\right)
\right)
,
\left(
\left(\log2+\log\left|\sin\frac{\theta}{2}\right|\right)\sin \theta
+\frac{\pi-\theta}{2}
\cos \theta\right)
\right)
}$
となります。
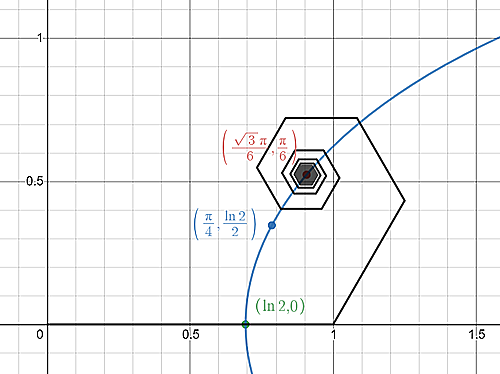
たとえば、${\displaystyle \theta=\frac{\pi}{3}}$ のときはアリのゴールは ${\displaystyle \left(\frac{\sqrt{3}\pi}{6},\frac{\pi}{6}\right)}$ となります。
Crazy Ant Problem の答え
つまり、最初の Crazy Ant Problem の答えは ${\displaystyle \left(\frac{\sqrt{3}\pi}{6},\frac{\pi}{6}\right)}$ということです。
また、回転する角度が90度、つまり ${\displaystyle \theta=\frac{\pi}{2}}$ のときは、 ${\displaystyle \left(\frac{\pi}{4},\frac{\ln 2}{2}\right)}$ に、回転する角度が180度、つまり ${\displaystyle \theta=\pi}$ のときは、 ${\displaystyle \left(\ln 2,0\right)}$ にそれぞれ収束することがわかります。なんだか神秘的ですね!
 CrazyAntAns
CrazyAntAns
フーリエ級数との関係
ところで、フーリエ級数というものがあります。簡単に言うと、関数をサイン波とコサイン波の和として表すというものです。こんな感じです。($f(x)$は周期$2\pi$の周期関数)
${\displaystyle f(x)=\frac{a_0}{2} + \sum_{k=1}^\infty (a_k\cos kx+b_k\sin kx)}$
ここであらためて、Crazy Ant Problem の収束先の$x$座標と$y$座標を表す式を級数の形に書き直してみましょう。
$x$座標
${\displaystyle
\left(\frac{\pi-\theta}{2}\sin\theta-
\left(
\log2+\log\left|\sin\frac{\theta}{2}\right|\right)\cos \theta
\right)
=1+\sum_{k=1}^{\infty}\frac{\cos k\theta}{k+1}
}$
$y$座標
${\displaystyle
\left(\frac{\pi-\theta}{2}
\cos \theta
+\left(\log2+\log\left|\sin\frac{\theta}{2}\right|\right)\sin \theta
\right)
=0+\sum_{k=1}^{\infty}\frac{\sin k\theta}{k+1}
}$
おや?なんだかフーリエ級数の式とそっくりですね!実際、左辺をフーリエ級数展開したものが右辺だと解釈することが可能です。
$x$座標の方は$\{a_0,a_1,a_2,\cdots\}=\left\{2,\frac{1}{2},\frac{1}{3},\frac{1}{4},\cdots\right\}$,$\{b_1,b_2,b_3\cdots\}=\left\{0,0,0,\cdots\right\}$としてやればいいですし、$y$座標の方は$\{a_0,a_1,a_2,\cdots\}=\left\{0,0,0,0,\cdots\right\}$,$\{b_1,b_2,b_3,\cdots\}=\left\{\frac{1}{2},\frac{1}{3},\frac{1}{4},\cdots\right\}$としてやればいいですね。
フーリエ級数の係数を求める式で積分を作る
フーリエ級数の係数はこんな式で計算することができます。
${\displaystyle \begin{align} a_n &= {1 \over \pi} \int_{0}^{2\pi} f\left(t \right) \cos nt\,dt, \left(n = 0,1,2,3,\cdots \right) \\ b_n &= {1 \over \pi} \int_{0}^{2\pi} f\left(t \right) \sin nt\,dt, \left(n = 1,2,3,\cdots \right) \end{align} }$
先ほどの級数にこの式を適用することで、こんな式が得られます。
${\displaystyle \frac{1}{\pi}\int_0^{2\pi}\left(\frac{\pi-\theta}{2}\sin\theta- \left( \log2+\log\left|\sin\frac{\theta}{2}\right|\right)\cos \theta \right)\cos(n\theta)d\theta=\frac{1}{n+1}\qquad(n=1,2,3,\cdots) }$
${\displaystyle \frac{1}{\pi}\int_0^{2\pi}\left(\frac{\pi-\theta}{2}\cos \theta +\left(\log2+\log\left|\sin\frac{\theta}{2}\right|\right)\sin \theta \right)\sin(n\theta)d\theta=\frac{1}{n+1}\qquad(n=1,2,3,\cdots) }$
こんな複雑な積分の計算結果が、(マジメに計算することなく)求めることができてしまいました!面白いですね!
