算術四面体
算術三角形を立体にする
算術三角形は上の二つの数字を足して新しい段を作ります。では、うえの三つの数字を足してできる図形はどうなるでしょうか。
まず、0段目に1を置きます。
算術四面体0
さて、算術三角形では二方向に1が並んでいきました。今考えているのは上の三つの数字を足すものになりますので、1は三方向に並んでいきます。1段目には1が三つ置かれます。
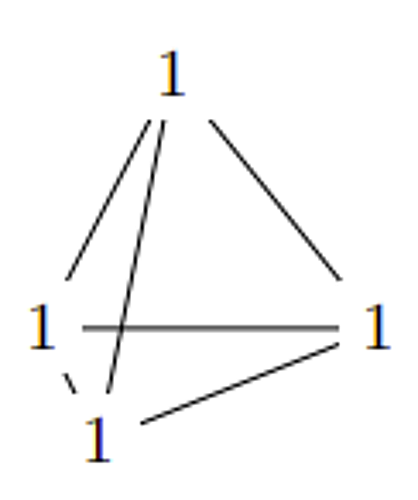算術四面体1
次の段では少し注意が必要です。一見すると真ん中に3があると思いかねませんが、1段目の1からそれぞれ三方向に線を伸ばすと下図のようになることがわかります。
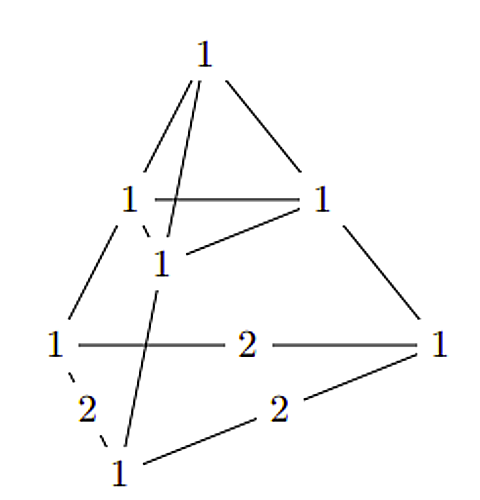算術四面体2
3段目も同様に考えれば下図のようになります。
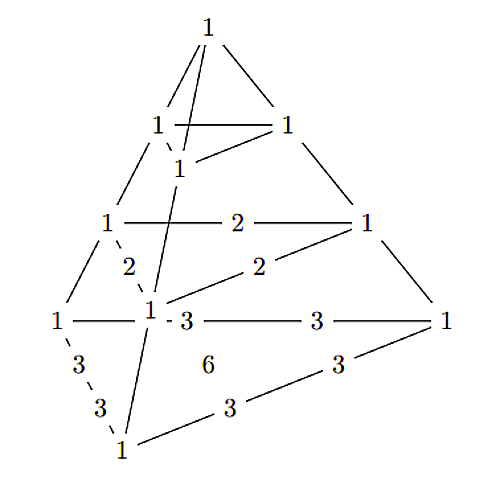算術四面体3
4段目にもなると数字が増えてきて度の数字がどの段にあるかわかりにくくなってきますね。
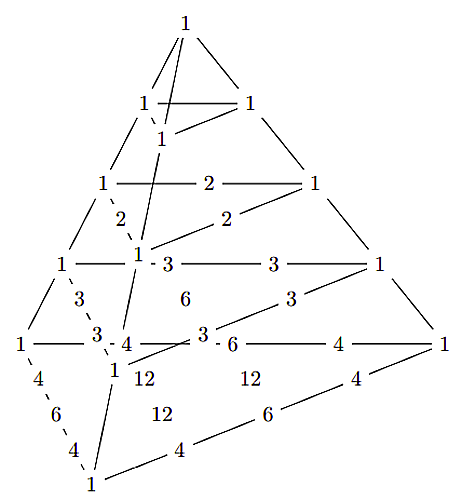算術四面体4
このように作られる図形を算術四面体と呼ぶことにしましょう。
多項定理（三項定理）
二項定理によれば、$(x+y)^n$を展開したときの係数が算術三角形のにあらわれます。では算術四面体の各項で似たようなことを考えられないでしょうか。
実は算術四面体の各項は$(x+y+z)^n$の係数になります。具体的に見てみましょう。
$\begin{align*} (x+y+z)^0&=1\\ (x+y+z)^1&=x+y+z\\ (x+y+z)^2&=x^2+y^2+z^2+2xy+2yz+2zx\\ (x+y+z)^3&=x^3+y^3+z^3+3x^2y+3y^2z+3z^2x+3xy^2+3yz^2+3zx^2+6xyz\\ (x+y+z)^4&=x^4+y^4+z^4+4x^3y+4y^3z+4z^3x+6x^2y^2+6y^2z^2+6z^2x^2+4xy^3+4yz^3+4zx^3+12x^2yz+12y^2zx+12z^2xy \end{align*}$
4乗ともなると長くなりますね。ではその4乗と算術四面体の4段目を見比べてみると次のようになります。
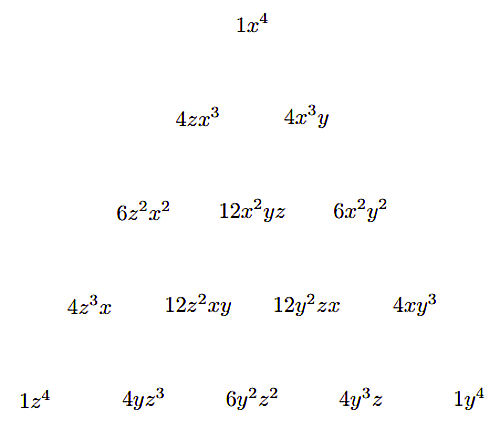多項定理
このように並べてみるとわかりやすくなるのではないでしょうか。ほかの段も同様にすれば、係数と算術四面体の各項が一致することがわかります。
一般に以下の定理が言えます。
任意の正整数$m$、非負整数$n$に対し、以下が成り立つ。
$$
(x_1+\dots+x_m)^n=\sum_{k_1+\dots+k_m=n}\frac{n!}{k_1!\cdots k_m!}x_1^{k_1}\cdots x_m^{k_m}
$$
特に三項の場合、$$
(x+y+z)^n=\sum_{i+j+k=n}\frac{n!}{i!j!k!}x^iy^jz^k
$$
となり、$\frac{n!}{i!j!k!}$が算術四面体の項を表す式になります。
さらに高次元へ
ここまで三角形から四面体へ次数を上げることを考えてきました。もちろん四次元、五次元、・・・と次元を上げていくことができます（ちょっと二次元に図を描くのは難しいのでやりませんが）。その場合、多項定理の$n=4$や$n=5$のときに相当します。したがって、図に描くことは難しくとも数式として扱っていくことは比較的容易です。
算術三角形には面白い性質があるので、それが次元を上げることによってどのような表現になるのか考えるのも楽しいと思います。