座標平面上の直線に対して対称な点の座標

数Ⅱの夏休み前の期末試験の範囲に図形と方程式の単元がありました。その当時の数学のノートを最近見つけたので見てみると、あらゆる公式を全部暗記して乗り切ろうと思っていたらしく、このような問題を作って公式を導出していました。今回はここにそれを紹介したいと思います。

解答の指針

$\mathrm{P,Q}$は、直線$\ell$に対して対称であるから、線分$\mathrm{PQ}$の中点$\mathrm{M}$は$\ell$上にあります。

そこで、次のような手順で考えていきます。

1. $\mathrm{Q}$の座標を仮定して、中点$\mathrm{M}$の座標を表す。
2. $\mathrm{M} $が$\ell$上にあるので、それを元に式を一つ作る。
3. 直線$\ell$と線分$\mathrm{PQ}$は垂直なので、それを元にもう一つ式を作る。
4. 2、3を連立して所望の座標を得る。

それではやっていきたいと思います。

解答

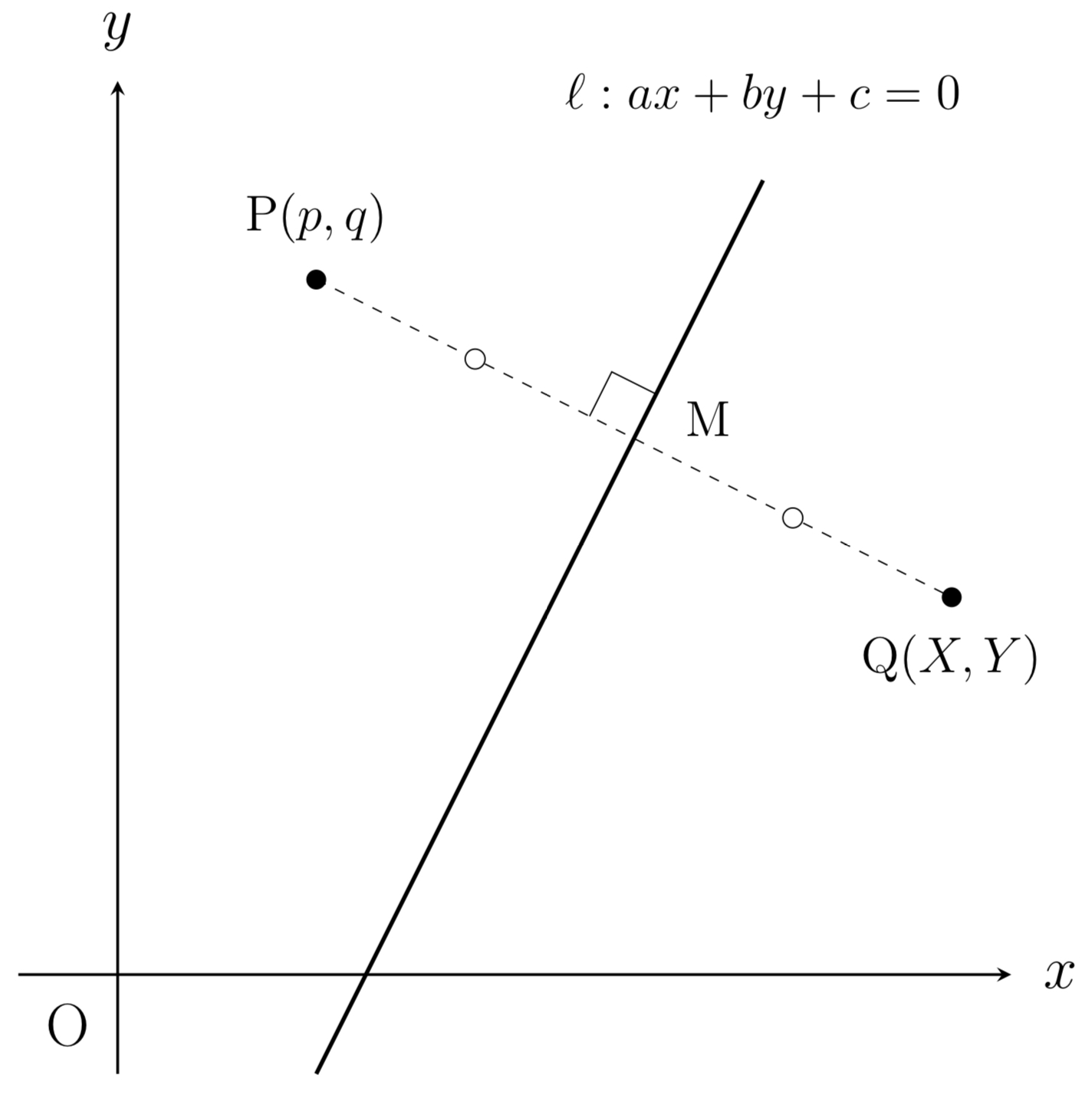状況を図に表してみる
求める$\mathrm{Q}$の座標を$(X,Y)$とする。

ここで、線分$\mathrm{PQ}$の中点$\mathrm{M}$の座標は、$\left(\cfrac{p+X}{2},\cfrac{q+Y}{2} \right)$である。

この$\mathrm{M}$が$\ell:ax+by+c=0$上にあるので、代入して整理すると

$$a\left(\cfrac{p+X}{2} \right)+b\left(\cfrac{q+Y}{2} \right)+c=0 $$

$$aX+bY=-ap-bq-2c$$

また、$\ell\bot\mathrm{PQ}$より、傾きの積が$-1$となる。それぞれ、
$$\ell:-\cfrac{a}{b}(\because\ y=-\cfrac{a}{b}x—\cfrac{c}{a} )$$

$$\mathrm{PQ}:\cfrac{Y-q}{X-p}$$

であるから、

$$-\cfrac{a}{b}\cdot \cfrac{Y-q}{X-p}=-1 $$

$$bX-aY=bp-aq$$

を得る。

よって、

$$\begin{pmatrix} a &b \\ b &-a \end{pmatrix} \begin{pmatrix} X \\ Y \end{pmatrix} = \begin{pmatrix}-ap-bq-2c \\ bp-aq \end{pmatrix} $$

を解けば良い。これを$A\vec{x}=\vec{b}$とおく。

補足

高校時代の自分は、背伸びをしまくって自分を誇張したがる高二病重症患者だったので、数学できるぜアピールをするためにチャート式をいつも座右に置いていました。なので、数学Cでやる予定の行列については、一通り読んでいて、連立方程式とかも行列を使って解いていました。
ここでは、その当時のやり方に従って、連立方程式を解いていきます。（補足終）

ここで、行列$A$について、$\Delta=-a^{2}-b^{2}$である。
この連立方程式がただ一つの解を持つには、$\Delta\ne 0$でなければならない。
そこで、$\Delta=0$の場合を考えると、
$\Delta=0\Leftrightarrow -a^{2}-b^{2}=0$
$a^{2}=-b^{2}$
であり、これを満たすのは$a=b=0$の場合だけである。そして、このときの$\ell$は$c=0$でもはや直線ではない。
よって、任意の直線で$\Delta=-a^{2}-b^{2}\ne 0$であることが言える。
これより、$A$の逆行列は$$A^{-1}=\cfrac{1}{a^2+b^2}\begin{pmatrix} a &b \\ b &-a \end{pmatrix}$$
である。よって、求める$\mathrm{Q}$の座標は$\vec{x}=A^{-1}\vec{b}$を解くことで、

$$\begin{pmatrix} X \\ Y \end{pmatrix} =\cfrac{1}{a^2+b^2}\begin{pmatrix} a &b \\ b &-a \end{pmatrix} \begin{pmatrix}-ap-bq-2c \\ bp-aq \end{pmatrix} $$

$$\begin{pmatrix} X \\ Y \end{pmatrix} =-\cfrac{1}{a^2+b^2} \begin{pmatrix} a(ap+bq+2c)+b(aq-bp) \\ a(bp-aq)+b(ap+bq+2c) \end{pmatrix} $$

$$\begin{pmatrix} X \\ Y \end{pmatrix} =-\cfrac{1}{a^2+b^2} \begin{pmatrix} (a^{2}-b^{2})p+2abq+2ca \\ 2abp-(a^{2}-b^{2})q+2bc \end{pmatrix} $$

となる。

ちょこっと練習

さっそくこの公式を使ってみましょう。

解答

先の公式で、$a=2,b=-1,c=-1,p=0,q=4$を代入すれば良い。
よく出るファクターの計算を先にしておくと、
$a^{2}+b^{2}=2^{2}+(-1)^{2}=4+1=5$
$a^{2}-b^{2}=2^{2}-(-1)^{2}=4-1=3$
$2ab=2\cdot 2\cdot (-1)=-4$

よって、求める座標は
$$\left(-\cfrac{3\cdot0-4\cdot 4+2\cdot2\cdot(-1)}{5},-\cfrac{-4\cdot0-3\cdot4+2\cdot(-1)\cdot(-1)}{5} \right)$$

$$=\left(-\cfrac{-20}{5},-\cfrac{-10}{5} \right)$$

$=(4,2)$
である。

これで、機械的に計算できるようになりましたね。

後日談

これを覚えて期末試験に臨んだわけですが、出題範囲が三角関数までと広すぎたので、直線に対称な点の問題は1問だけで、3点分しか出ず、コスパがあまりにも悪すぎました。

ていうか、公式を使わなくても、上の指針に従って計算すれば答えが出せたし、むしろその方が解き終えるのが早かった覚えがあります。

公式は機械的に覚えるものではなく、繰り返しの練習で身につけるものなんだな、と改めて感じましたし、教科書に載っている例題のやり方にはきちんと意味があるのだなとも思いました。この公式を得る過程で様々な学びを得られたと思いたい。

よって、あの当時もがき苦しみながら作り出したのに、全く使われることもなく、その努力が報われることがないまま古びていったこの公式が、いつか他の誰かの役に立つ日が来ることを祈念して、この記事の結びとします。