TMO13の一般化について
筑駒の数学研究部の方々が文化祭に開催している数学コンテスト,TMOが今年も開催され面白い問題が揃っていた.大トリの第$13$問が初等幾何で含蓄のある問題だったので,私なりの答案を示しておく.なお,問題自体は Xのこちらの投稿 から確認できる.まずは自分で手を動かして解いてみることをお勧めする.
皆様が問題を解いている間,踊っている有理数集合をお届けしておく.
₍₍⁽⁽$\mathbb{Q}$₎₎⁾⁾
それでは問題を解いていこう.
問題をまず以下のように拡張する.
点$P$と直線$XY$の距離を$d(P,XY)$で表す.
三角形$ABC$の内部に点$D,E,F$を$d(E,AB)=d(F,CA), $
$d(F,BC)=d(D,AB),d(D,CA)=d(E,BC)$
を満たすように取る.三点$D,E,F$が同一直線$\ell$上にあるとき,三角形$ABC$の内心$I$も$\ell$上にある.
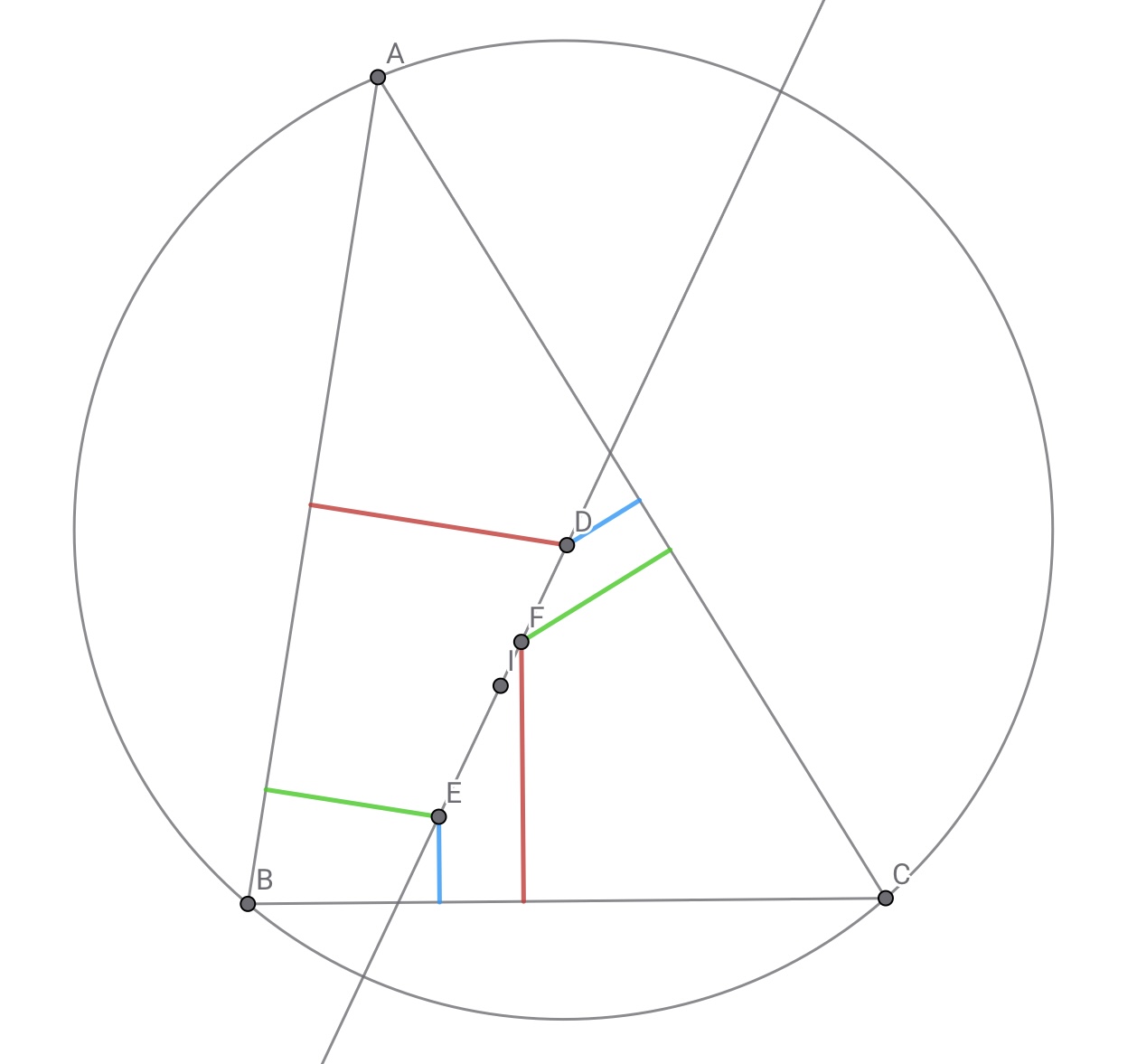 外接円は不要でしたね……
外接円は不要でしたね……
$D,E,F$は三角形$ABC$の内部である必要はないが,問題文の簡略化のために設定した.厳密性を突き詰めるなら直線に有向性を与え,点と直線の距離に正負の概念を持ち込む.
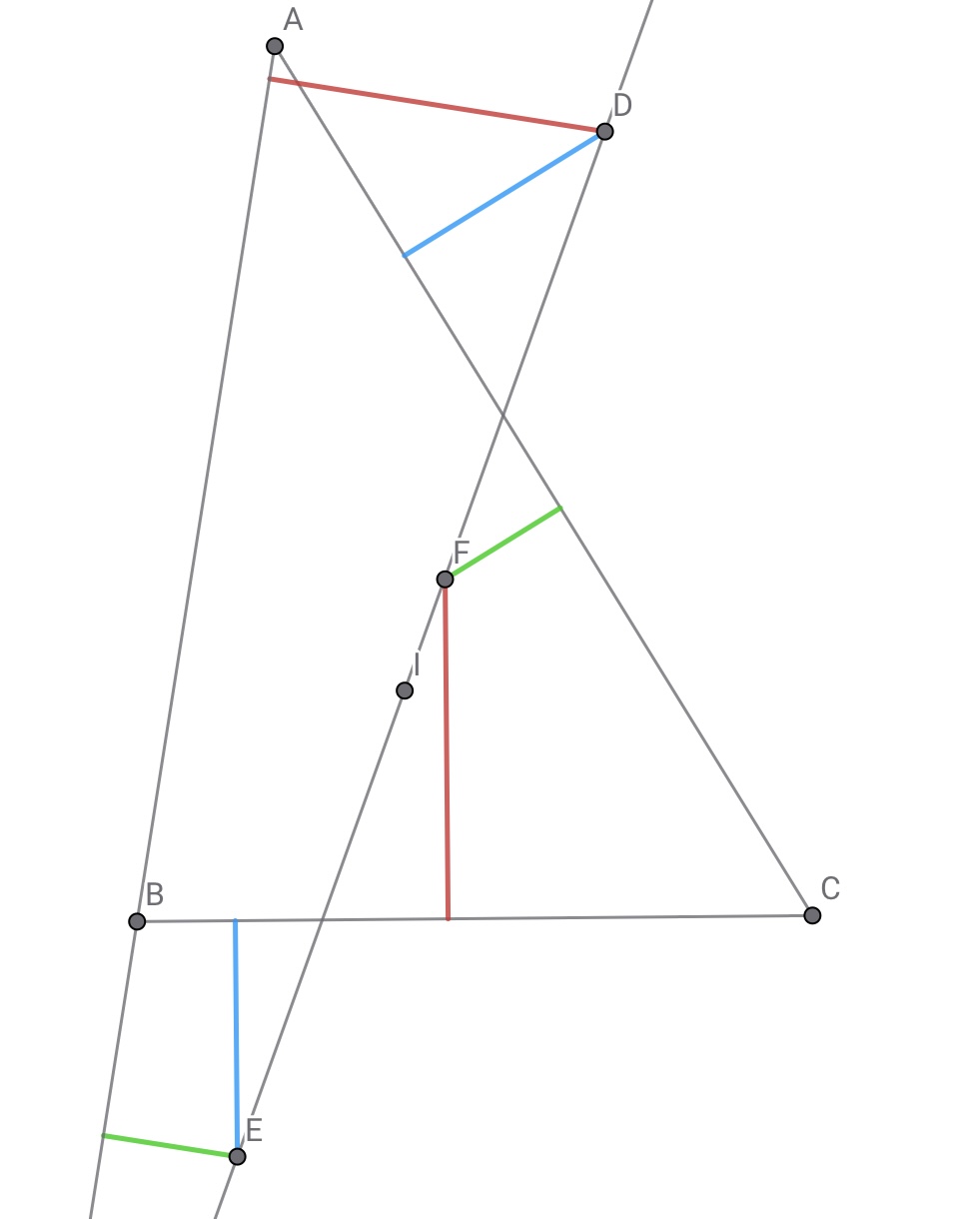 距離の正負がなんとなく分かるでしょうか
距離の正負がなんとなく分かるでしょうか
これが元の問題の一般化たりうることは演習問題としておきたい.
改題を示すにあたり,まずは直線$AD,BE,CF$が一点で交わることを示す.
直線$AD$と$BE$の交点を点$P$とすれば
$d(P,CA):d(P,AB):d(P,BC)=\dfrac{1}{d(D,AB)}:\dfrac{1}{d(E,BC)}:\dfrac1{d(E,AB)}$
より$d(P,CA):d(P,BC)=d(F,CA):d(F,BC)$
なので点$C,F,P$は同一直線上であり,直線$AD,BE,CF$は一点$P$で交わる.
![この性質は!FORMULA[25][-420088591][0]が同一直線上である必要性はない](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUFoBEqHFmgiOPf3KPL4E.jpeg?alt=media) この性質は$D,E,F$が同一直線上である必要性はない
この性質は$D,E,F$が同一直線上である必要性はない
距離の比に逆数が出てきたことから次の一手の予想がつくと思われるが,ここでいくつかの補助点などを設定しておこう.
- 三角形$ABC$における点$P$の等角共役点を点$Q$とする.
- 直線$AI,BI,CI$が三角形$ABC$の外接円と再び交わる点を順に$X,Y,Z$とする.
- 直線$YZ$に関して点$D$を対称移動させた点を$D’$,直線$ZX$に関して点$E$を対称移動させた点を$E’$,直線$XY$に関して点$F$を対称移動させた点を$F’$とする.
![煩雑になるので直線!FORMULA[41][724935673][0]は省略](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FHTsI4hCySYUz9o4mKvBn.jpeg?alt=media) 煩雑になるので直線$AI,BI,CI$は省略
煩雑になるので直線$AI,BI,CI$は省略
等角共役より$\dfrac{d(Q,BC)}{BQ}:\dfrac{d(Q,BC)}{CQ}=\dfrac{d(E,AB)}{BE}:\dfrac{d(F,CA)}{CF}$
を用いて$AQ:BQ:CQ=AD:BE:CF$となる.
基本的な性質として,直線$YZ,ZX,XY$はそれぞれ線分$AI,BI,CI$の垂直二等分線であることから上記と合わせて
$AQ:BQ:CQ=D’I:E’I:F’I$および$AQ/\!/D’I,BQ/\!/E’I, CQ/\!/F’I$が分かる.したがって三角形$ABC$と三角形$D’E’F’$は拡大縮小のみで重なり合う相似であり,直線$AD’,BE’,CF’,QI$は相似の中心$T$で交わる.
![この性質も!FORMULA[52][-420088591][0]が同一直線上である必要性はない](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FCnDA67dlwWFt4RJ3o3TT.jpeg?alt=media) この性質も$D,E,F$が同一直線上である必要性はない
この性質も$D,E,F$が同一直線上である必要性はない
ここで直線$DE$を直線$YZ,ZX$に関して対称移動させた直線を順に$\ell_1,\ell_2$とし,$\ell_1$と$\ell_2$の交点を$T’$とすれば,$\ell_1$は点$D’$を,$\ell_2$は点$E’$を通り,角度追跡から$\angle E’T’D’=180\degree-2\angle YZX=\angle BCA=\angle E’F’D’$より四点$D’,E’,F’,T’$は同一円周上である.(厳密な議論では有向角を用いたい)
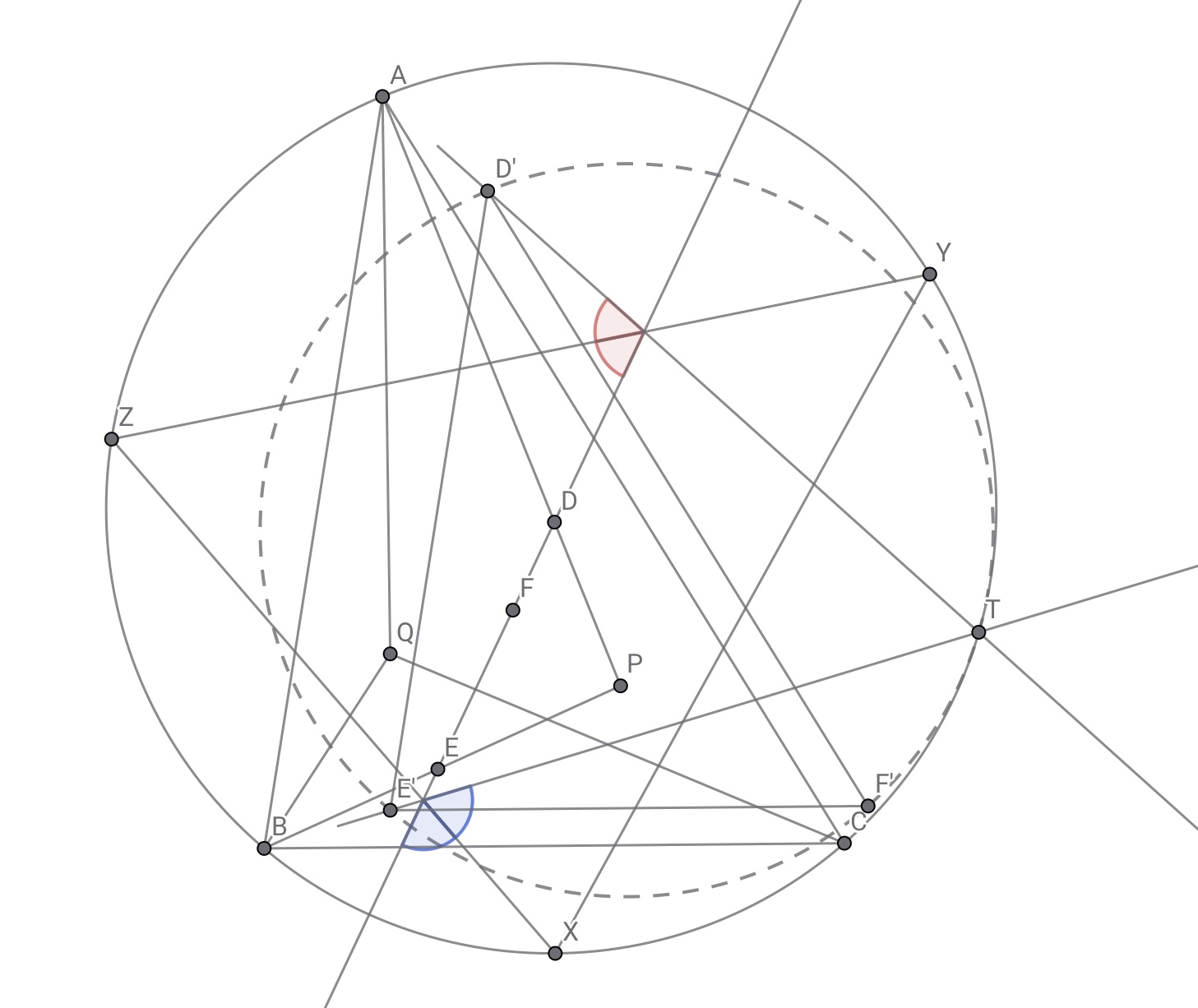 Tと書かれていますがT’の誤りです……
Tと書かれていますがT’の誤りです……
三点$D,E,F$が同一直線上であるとき,$\ell$を直線$XY$に関して対称移動させた直線を$\ell_3$とすれば,$\ell_1$と$\ell_2$の交点,$\ell_2$と$\ell_3$の交点,$\ell_3$と$\ell_1$の交点はいずれも三角形$D’E’F’$の外接円上にとなる.これは三直線$\ell_1,\ell_2,\ell_3$が三角形$D’E’F’$の外接円上で一点で交わる,もしくはこの三直線の組が三直線$D’E’,E’F’,F’D’$の組と一致するのいずれかとなるが,後者の場合は直線$\ell$が直線$AB,BC,CA$の全てと平行でなければならず矛盾.したがって,三直線$\ell_1,\ell_2,\ell_3$は一点で交わることがわかる.この点を$S$とすれば,直線$\ell$は点$S$から三角形$XYZ$へのシュタイナー線となることがわかり,これは三角形$XYZ$の垂心,すなわち三角形$ABC$の内心$I$を通る.
上記において点$S$と点$T$は一致することがわかり,点$P$が与えられたとき(元の問題では三角形$ABC$の垂心$H$),この点の三角形$ABC$における等角共役点$Q$(元の問題では三角形$ABC$の外心$O$)と内心$I$を結ぶ直線を引き,この直線と三角形$ABC$の外接円の交点$T$から三角形$XYZ$にシュタイナー線を引いて直線$AP,BP,CP$との交点を順に$D,E,F$とすれば良い.
![点!FORMULA[104][-420088591][0]は「2組」あったッ!](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUy6UyZMBUtHfPA64FqGD.jpeg?alt=media) 点$D,E,F$は「2組」あったッ!
点$D,E,F$は「2組」あったッ!
と言うわけでTMO2025-13を堪能してみた.筑駒の数学研究部をはじめオンラインで活動されている多くの方々,レベルの高い問題を各分野揃えたコンテストを開いてくださりありがとうございます.