高校数学解説

文献あり

美術館定理

139

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

はじめに

美術館定理を示す機会があったので色々調べたところネット記事には行間を十分埋めているものが確認したところなかったので高校生でも読めるようにきちんとした証明を書いてみました。

数学的帰納法と背理法

ここは分かっている人は読み飛ばしていい。

数学的帰納法

自然数 $n$ に関する条件 $P_{n}$ から作られる全称命題
$\begin{array}{r} 任意の自然数 n に対し, P_{n} \end{array}$
が成り立つことを示すために以下の方法がある。

$P_{1}$ が成り立つことを示す。
任意の自然数 $k$ に対し, $P_{k}$ ならば, $P_{k + 1}$ が成り立つことを示す。

このような証明方法を数学的帰納法という。

数学的帰納法の改良版

自然数 $n$ に関する条件 $P_{n}$ から作られる全称命題
$\begin{array}{r} 任意の自然数 n 対し, P_{n} \end{array}$
が成り立つことを示すために以下の方法がある。

$P_{1}$ が成り立つことを示す。
任意の自然数 $k$ に対し, $P_{1}, P_{2}, \dots, P_{k}$ ならば, $P_{k + 1}$ が成り立つことを示す。

背理法

命題 $P$ が真であることを証明するために, $P$ が成り立たない、つまり命題「 $P$ でない」が成り立つと仮定して、矛盾が導かれることを示す、という方法。矛盾とは, ある命題 $P$ とその否定命題「 $P$ でない」が同時に真であることをいう

美術館定理とその大まかな証明

まず断っておくこととして, この記事での多角形は凸多角形と凹多角形の両方を指します。高校までは多角形と書いたら凸多角形しか指さないですが本記事ではそうすることにします。それと美術館定理の主張以降は度数法ではなく弧度法を用います。

美術館定理

$n$ 角形でできている美術館に $360^{\circ}$ 見渡せる監視カメラをいくつか設置して美術館全体を監視できるようにしたい。このとき $[\frac{n}{3}]$ 台あれば十分である。ただし,実数 $x$ に対し $[x]$ は $x$ を超えない最大の整数を表す。すなわち $[]$ はガウス記号。

具体例を出して説明しないとわからないと思うので, 例を出してみます。

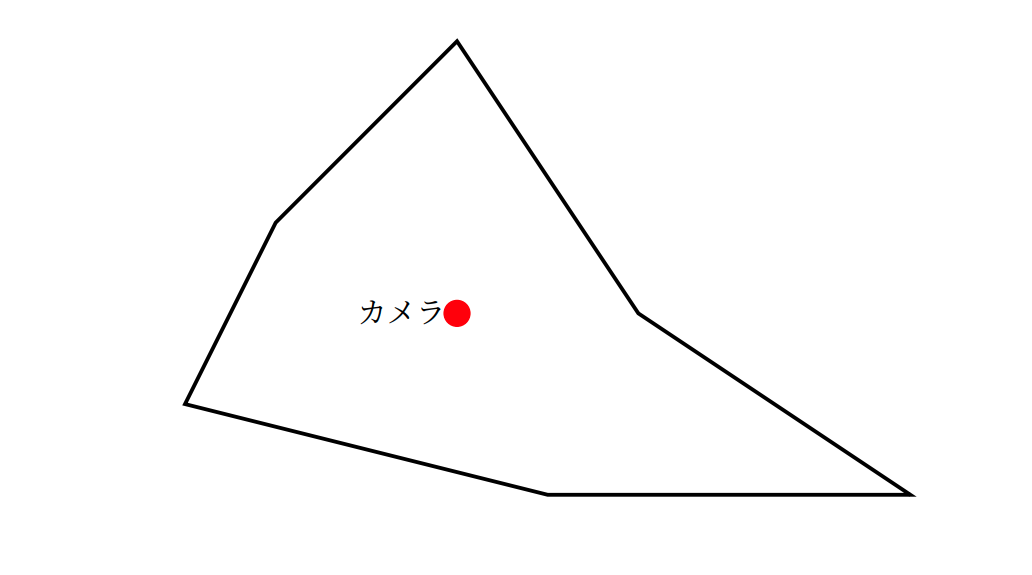この美術館は1つのカメラですべてを見渡せます。

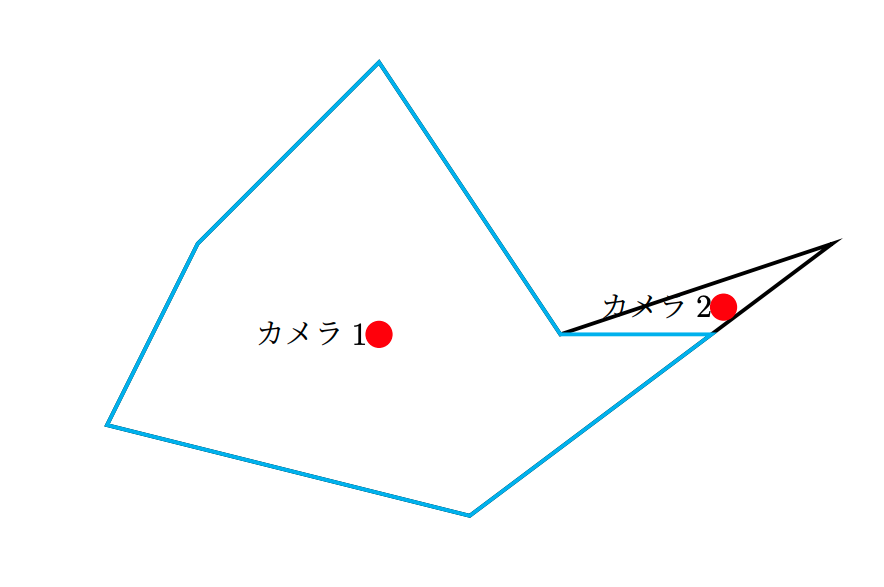カメラ1だけでは青色で囲んだ領域までしか見渡せない。

では, この定理を色々なことを認めながら証明していきます。
まず最初に

任意の多角形は三角形分割可能である

$n ≧ 4$ ならば $n$ 角形は $n - 3$ 本の対角線をうまく選んで $n - 2$ 個の三角形に分割できる。

という定理を認めます。これは凸多角形の場合に限定すると自明ですね。凹多角形が面倒。
三角形分割の例

さらに, 多角形の各頂点に赤, 青, 緑のいづれかを塗ってみるにします。ただし, 隣り合う頂点は異なる色でそしてどの色も一回は使うことにします。このような塗り方で多角形の各頂点に色を塗ることを三彩色するということにします。
三彩色の例

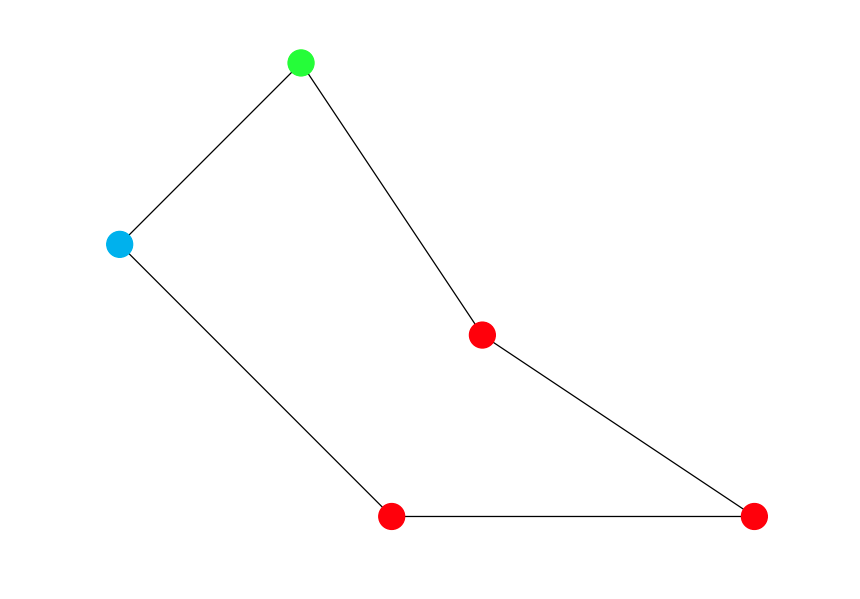三彩色ではない彩色の例（赤が隣合っている）

どんな多角形も三彩色できます。なぜなら, $n$ 角形 ${A_{1} A_{2} \dots A}_{n}$ が与えられたら, 頂点 ${A_{1}, A_{2}, \dots, A}_{n - 1}$ には赤, 青を交互に塗り, $A_{n}$ には緑を塗ることで三彩色の一つが得られるからです。以下が $n = 5$ の例
三彩色は可能であることの図（!FORMULA[35][36584066][0]）三彩色は可能であることの図（ $n = 5$ ）

では, 美術館定理の証明のために多角形にもう少し厳しい三彩色ができることを認めてみます。

$n ≧ 4$ とする。 $n$ 角形を $n - 2$ 個の三角形で分割する。この各三角形が三彩色された $n$ 角形を三彩色する方法が存在する。

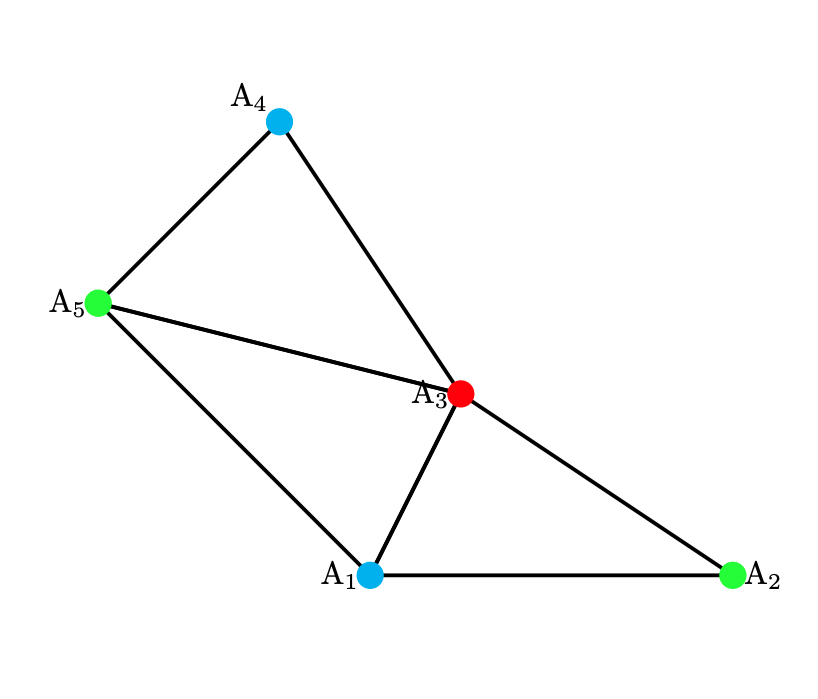定理6の特別な三彩色の例

では美術館定理を証明してみましょう。

美術館定理の証明

$n$ 角形を三彩色してみます。するとどの色かは分からないけど, 少なくとも一つの色は $[\frac{n}{3}]$ 個以下の頂点にしか彩色していません。なぜならどの色も $[\frac{n}{3}] + 1$ 個以上の頂点に彩色していると仮定すると
$\begin{array}{r} 3 ([\frac{n}{3}] + 1) > n \end{array}$
となりそんな三彩色の方法は存在ないので矛盾（背理法を用いている）。ここで三彩色と言っても定理3の三彩色を $n$ 角形にしていると仮定します。どの色かは分からないけど $[\frac{n}{3}]$ 個以下の頂点にしか彩色していない色があるので, その各頂点に監視カメラを設置してみます。すると, 各監視カメラは（美術館全体を見渡すことはできないかもしれないけど）その監視カメラが置かれている頂点をもつ（三角形分割で作られた）三角形の領域では完全に見渡すことができます。したがって, 今置いたすべての監視カメラで美術館全体を見渡すことができます。

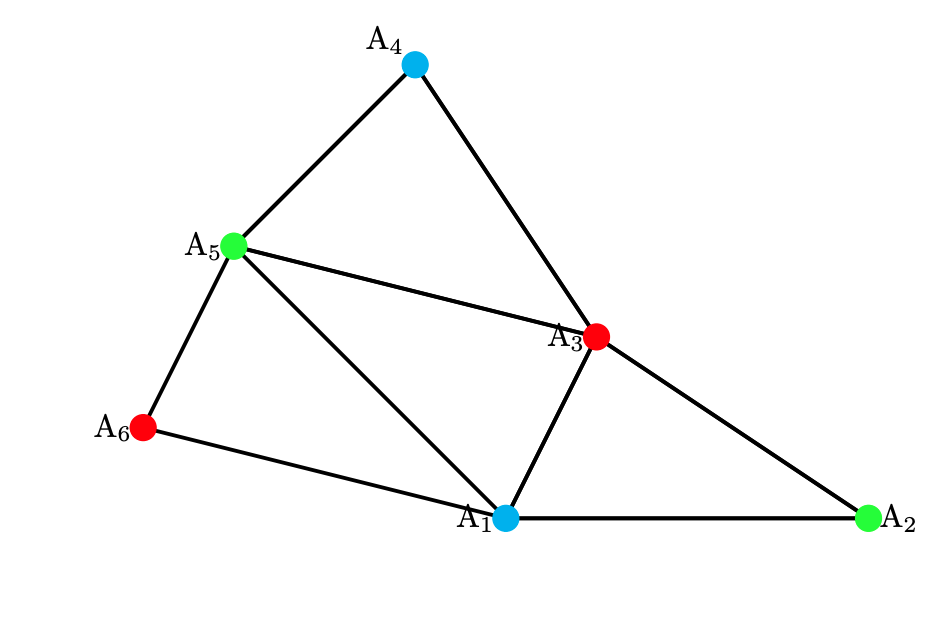美術館定理解決の図（この場合はどの色にカメラを設置してよい）

定理6の特別な三彩色の例として紹介した例では赤にカメラを設置すればよい

認めた定理の証明

まず三角形分割の方から示そう。

n

角形の内角の大きさの和は

(n - 2) π

$n$ 角形の内角の大きさの和は $(n - 2) π$ である。

$n$ 角形の外角の大きさの和は $2 π$ である。それゆえ内角の大きさの和は $n π - 2 π = (n - 2) π$ である。この式の意味は, $n π$ は各頂点の内角と外角の大きさの和が $π$ であることと頂点が $n$ 個であることと, そこから外角の大きさの和 $= 2 π$ を引いていることから来ている。

開線分と耳

両端を含まない線分を開線分という。多角形 $P$ の連続する3つの頂点 $A, B, C$ に対し, 開線分 $AC$ が $P$ の内部に含まれるとき, $△ ABC$ を $P$ の耳という。

例を見てみましょう。

凸四角形とその耳

凹四角形とその耳

この凹四角形に対し以下の周を緑で塗った三角形は耳ではありません。

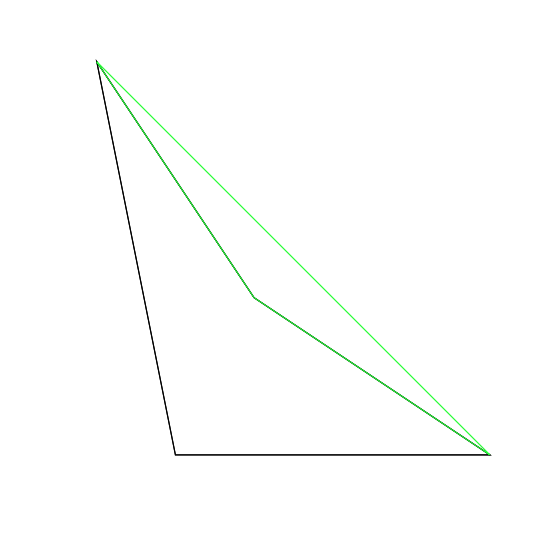凹四角形とその耳でない三角形

耳定理

$n ≧ 4$ なら, $n$ 角形は（辺は共有することは
あってもそこに目を瞑れば）互いに重なり合わない耳を2つ以上持つ。

例を見てみます。

どの2つの耳も辺は共有することはあっても互いに重なり合っていない。

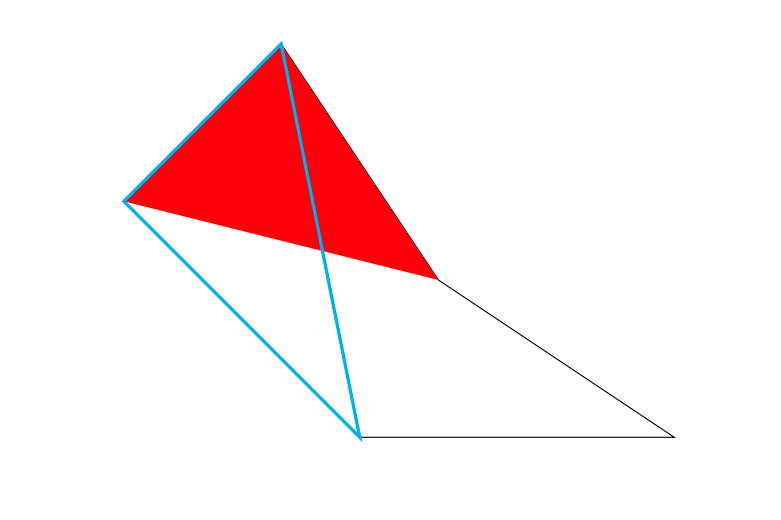互いに重なり合ってしまっている耳たち

数学的帰納法で示す

$n = 4$ のときは上記の例で見たように成り立ちます。2つ以上の内角の大きさが $π$ より大きくなることはありません。それはそのような四角形が存在すると仮定すると内角の和が $2 π$ より大きくなり命題7（内角の和の大きさの和の公式）と矛盾するからです。

$n ≦ k$ のとき成り立つと仮定する。 $k + 1$ 多角形 $P$ とその内角の中で大きさが $π$ 未満のものの1つを $∠ B$ とし, その両隣の頂点をそれぞれ $A, C$ とする。

開線分 $AC$ が $P$ の内部に含まれるとき。このとき, $△ ABC$ は $P$ の耳です。そして $P$ は $△ ABC$ と $P$ から $△ ABC$ を除いてできる $k$ 角形でできている図形です。この $k$ 角形は帰納法の仮定から互いに重なり合わない耳を2つ以上もちます。ゆえに $P$ は互いに重なり合わない耳を2つ以上もちます。
開線分 $AC$ が $P$ の内部に含まれないとき。このとき $△ ABC$ の内部には $P$ の頂点が含まれている。この中で $B$ と「最も近い」点の一つを $X$ とする。詳しくいうと, $△ ABC$ の内部の各点に対し開線分 $AC$ に平行な直線を引きます。すると, 点 $B$ とその各直線との距離が考えられらます。その中で最も $B$ と近い直線上の $P$ の頂点のうちの一つを $X$ とします。線分 $BX$ によって $P$ を2つの多角形に分割します。するとどちらかの多角形は頂点数が $4$ 以上かつ $k$ 以下の多角形なので帰納法の仮定から互いに重なり合わない耳を2つ以上もちます。ゆえに $P$ は互いに重なり合わない耳を2つ以上もちます。
以上から, 耳定理（ $n ≧ 4$ なら, $n$ 角形は互いに重なり合わない耳を2つ以上持つ）が成り立つ。

これを利用すると

任意の三角形は三角形分割可能

$n ≧ 4$ ならば $n$ 角形は $n - 3$ 本の対角線をうまく選んで $n - 2$ 個の三角形に分割できる

を帰納法で得ることができる。

$n ≧ 4$ とする。 $n$ 角形を $n - 2$ 個の三角形で分割する。この各三角形が三彩色された $n$ 角形を三彩色する方法が存在する。

数学的帰納法で示す。

$n = 4$ のときは上述の例で述べたように成り立つ。

$n = k$ のとき成り立つと仮定して, $k + 1$ 角形でも成り立つことを示す。 $P$ を $k + 1$ 角形とする。三角形分割する。 $P$ の耳の一つを任意にとる。すると $P$ は, この耳と $P$ からそれを除いた $k$ 角形からなる図形だと思える。その $k$ 角形は帰納法の仮定から定理10（定理6）に書いてある三彩色ができるので, そのような彩色をする。 $P$ は任意に取った耳の一つの頂点のみまだ彩色していないので
その頂点の両隣と異なる色を塗る。この塗り方は, 定理10（定理6）に書いてある $P$ に対しての彩色の一つである。よって, $n = k + 1$ のときも成り立つ。
以上から, 定理10（定理6）が成り立つ。