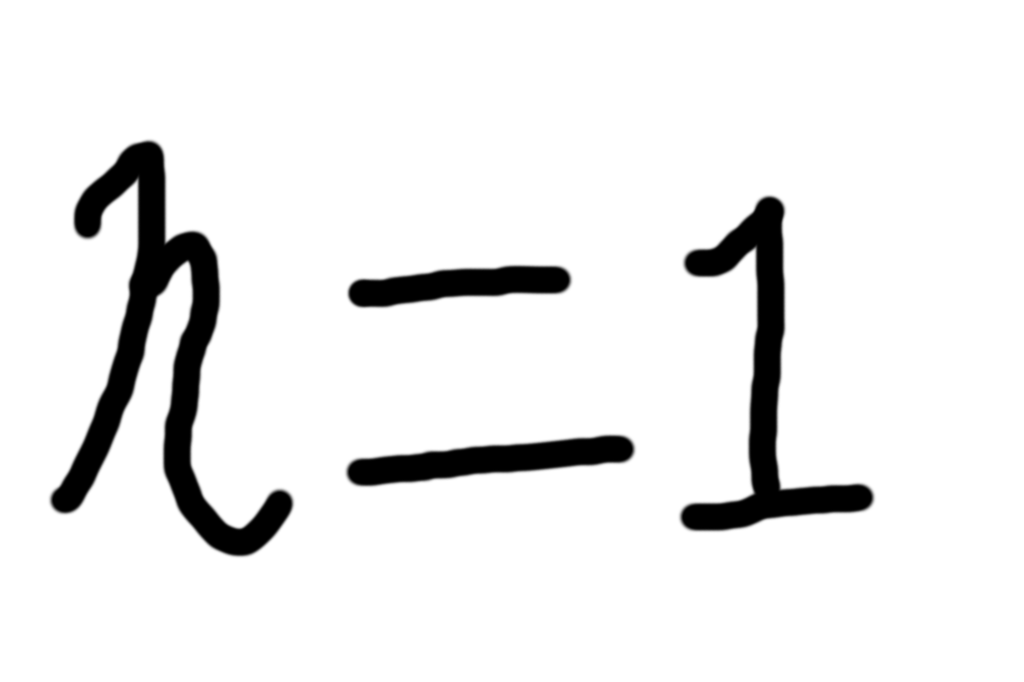sin1°、cos1°、tan1°の厳密値について

はじめに

　こんにち[加法の結果]、n=1です。今回は、$\sin1\degree,\ \cos1\degree, \tan 1\degree$の厳密値について求めていきます。

準備

　まず準有名角として、$15\degree, 18\degree$の場合の三角関数の値を以下にまとめておきます。

3倍角の定理は以下の通りです。

$\frac{1}{3}$倍角の公式

$3\degree$の場合求める

では加法定理を使って$3\degree$の場合のそれぞれを求めましょう。

$$ \begin{equation} \begin{aligned} \sin 3\degree&=\sin(18\degree-15\degree) =\sin18\degree \cos15\degree -\cos18\degree\sin15\degree\\ &=\frac{-1+\sqrt{5}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4} - \frac{\sqrt{10+2\sqrt{5}}}{4} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \\ &=\frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16} \qquad (=\frac{-\sqrt{2}-\sqrt{6}+\sqrt{10}+\sqrt{30}+2\sqrt{2(10-5\sqrt{3}+2\sqrt{5}-\sqrt{15})}}{16}) \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{aligned} \cos 3\degree&=\cos(18\degree-15\degree) =\cos18\degree \cos15\degree +\sin18\degree\sin15\degree\\ &=\frac{\sqrt{10+2\sqrt{5}}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4} + \frac{-1+\sqrt{5}}{4} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \\ &=\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16} \qquad (=\frac{\sqrt{2}-\sqrt{6}-\sqrt{10}+\sqrt{30}+2\sqrt{2(10+5\sqrt{3}+2\sqrt{5}+\sqrt{15})}}{16}) \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{aligned} \tan 3\degree&=\cos(18\degree-15\degree) =\frac{\tan18\degree-\tan15\degree}{1+\tan18\degree\tan15\degree}\\ &=\frac{\frac{\sqrt{25-10\sqrt{5}}}{5}-(2-\sqrt{3})}{1+\frac{(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}{5}} \\ &=\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}} \qquad (= \frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}) \end{aligned} \end{equation} $$

$1\degree$の場合を求める

　$\frac{1}{3}$倍角の公式①より、3次方程式を解き以下が示せます。

$\omega$は半角の公式の正負のように$\theta$の値から基本的には分かるのですが、今回は$\sin$は$\omega=\frac{-1-i\sqrt{3}}{2}$、$\cos$は$\omega=1$、$\tan$は$\omega=\frac{-1-i\sqrt{3}}{2}$でした。

これにより
$$ \begin{equation} \begin{aligned} \sin 1\degree&=\sin\frac{3\degree}{3}=\frac{\omega\sqrt[3]{-\sin3\degree+i\cos3\degree}+\omega^2\sqrt[3]{-\sin3\degree-i\cos3\degree}}{2}\\ &=\frac{1}{2}((\frac{-1-i\sqrt{3}}{2})\sqrt[3]{-(\frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})+i(\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})}+(\frac{-1+i\sqrt{3}}{2})\sqrt[3]{-(\frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})-i(\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})}) \\ &=\frac{1}{8}(-(1+i\sqrt{3})\sqrt[3]{\frac{((1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{2})+i((-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2})}{2}}+(-1+i\sqrt{3})\sqrt[3]{\frac{((1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{2})+i((1-\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{2})}{2}}) \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{aligned} \cos 1\degree&=\cos\frac{3\degree}{3}=\frac{\omega\sqrt[3]{\cos3\degree+i\sin3\degree}+\omega^2\sqrt[3]{\cos3\degree-i\sin3\degree}}{2}\\ &=\frac{1}{2}(\sqrt[3]{(\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})+i(\frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})}+\sqrt[3]{(\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})-i(\frac{(-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})}) \\ &=\frac{1}{4}(\sqrt[3]{\frac{((-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2})+i((-1+\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{6}+(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2})}{2}}+\sqrt[3]{\frac{((-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2})+i((1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}-\sqrt{10+2\sqrt{5}})\sqrt{2})}{2}}) \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{aligned} \tan 1\degree&=\tan\frac{3\degree}{3}=\tan3\degree+\frac{\omega \sqrt[3]{i+\tan3\degree}+\omega^2\sqrt[3]{-i+\tan3\degree}}{\cos^{\frac{2}{3}}3\degree}\\ &=\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}+(\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})^{-\frac{2}{3}}((\frac{-1-i\sqrt{3}}{2})\sqrt[3]{i+\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}}+(\frac{-1+i\sqrt{3}}{2})\sqrt[3]{-i+\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}}) \\ &=\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}+\frac{1}{\sqrt[3]{4+\sqrt{7+\sqrt{5}+\sqrt{6(5+\sqrt{5})}}}}(-(1+i\sqrt{3})\sqrt[3]{i+\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}}+(-1+i\sqrt{3})\sqrt[3]{-i+\frac{-10+5\sqrt{3}+\sqrt{25-10\sqrt{5}}}{5+(2-\sqrt{3})\sqrt{25-10\sqrt{5}}}})\\ &( \because (\frac{(-1+\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{6}+(1-\sqrt{5}+\sqrt{10+2\sqrt{5}})\sqrt{2}}{16})^{-\frac{2}{3}}=\frac{2}{\sqrt[3]{4+\sqrt{7+\sqrt{5}+\sqrt{6(5+\sqrt{5})}}}}) \end{aligned} \end{equation} $$

まとめ

　以上のことから$\sin1\degree,\ \cos1\degree,\ \tan1\degree$は以下の通りです。

最後に

　以上で今回のsin1°、cos1°、tan1°の厳密値については終わりです。間違っている部分がありましたらご指摘のほどお願いします。久しぶりの投稿となりましたが、投稿を見てくださりありがとうございました。