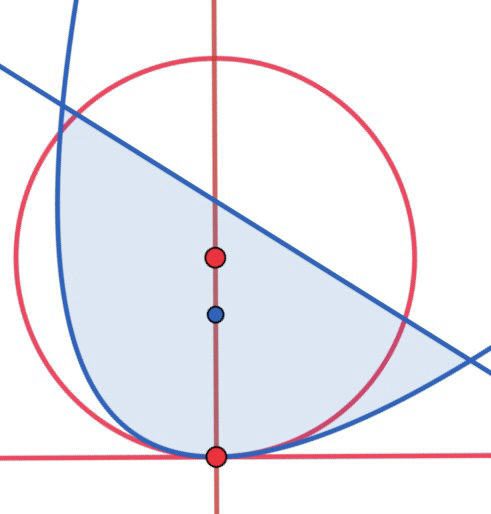
放物線で囲まれた物体の不安定なつりあい

はじめに

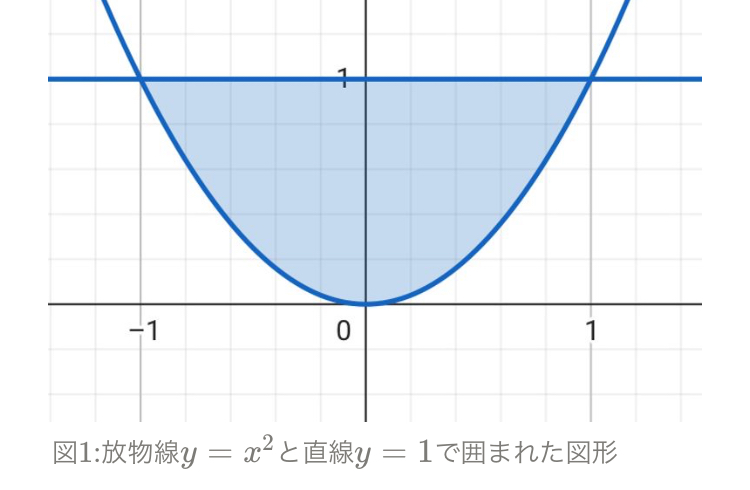
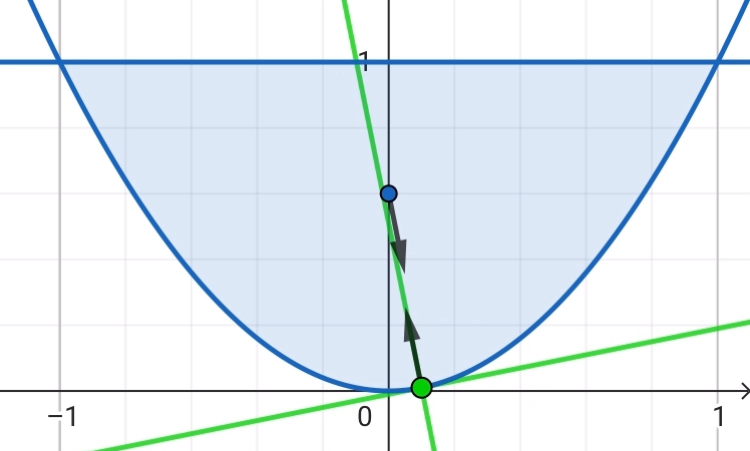
放物線$y=x^2$と直線$y=1$で囲まれた一様な物体について考える。この物体を放物線側を下にして床に置いた時にどこかには$1$番安定してつりあう接点があるはずだと考えた。そこで、そのような点が存在するとしたらどこにあるかを考える。また、頂点を接点として置いたとき、その点から少し右に倒すと垂直抗力の作用線より右に重心があると考えられるためさらに倒れる向きに力のモーメントが働くと推測した(図$2$)(動画$1$)。そこで、この点が本当にこのような性質を持ち、不安定なつりあいの点であるか、また、他に安定なつりあいの点が存在するとしたらどこにあるかを調べる。

頂点でのつりあいが不安定であること

ある曲線のある点における曲率円とは、簡単に言えばその点まわりのその曲線の曲がり具合を1番よく表した円である。例えば図$3$の円$O_1$は放物線$y=x^2$の点$\small O$における曲率円である。このとき、放物線上の点$\small O$に十分近い点$P$での法線(つまりその点を通り、接線に垂直な直線)と点$ O$における法線との交点は曲率円の中心$ O_1$に十分近い点となる$\small①$。
したがって、その点から少し倒れるとさらに倒れる向きに力のモーメントが働き、不安定なつりあいとなるということは、言い換えると、その点における曲率円の半径(つまり曲率半径)がその点と重心$ G$との距離より小さい$②$ということである(図$3$)。また、安定なつりあいとなるということは、曲率半径が重心との距離より大きいということで、曲率半径と重心との距離が等しいときは安定でも不安定でもない中立なつりあいとなる。
図$3$
まずこの物体の重心を求める。どのように求めるのかというと、重心の位置から回転体の体積を求めることができるパップスギュルダンの定理というものがある。この定理を逆手にとり、面積と回転体の体積から重心を求める。定理の主張は次のようなものである。

$y$軸対称より重心を$G(0,g)$この物体の面積を$S$、この物体の$y=1$まわりの回転体の体積を$V$とおくと$G$と$y=1$の距離が$1-g$よりパップスギュルダンの定理から$V=2\pi(1-g)S$が成り立つ。ここで$\displaystyle S=\int_{-1}^{1}(1-x^2)dx=\Big[ x-\dfrac{1}{3}x^3\Big]_{-1}^{1}=\dfrac{4}{3},V=\pi\int{-1}^{1}(1-x^2)^2dx=\pi\Big[\dfrac{1}{5}x^5-\dfrac{2}{3}x^3+x\Big]_{-1}^{1}=\dfrac{16}{15}\pi$から$g=1-\dfrac{V}{2\pi S}=\dfrac{3}{5}$となる。
したがって重心は$G(0,\dfrac{3}{5})$とわかる。
次に放物線$y=x^2$の原点における曲率半径を求める。
求める$y$軸対称より曲率円の中心は$O_1(0,r_1)$とおける。放物線上の点を$P(p,p^2)(p\ne0)$とし、放物線の$O$における法線つまり$x=0$と$P$における法線の交点を$O_p$とする。この時 $①$より$p→0$のとき$O_p→O_1$である。
$f(x)=x^2$とおくと$f’(x)=2x$から$P$における法線は$y=-\dfrac{1}{2p}x+p^2+\dfrac{1}{2}$とわかる。この直線と$x=0$の交点は$O_p(0,p^2+\dfrac{1}{2})$となる。ゆえに、$p→0$のとき$O_p→(0,\dfrac{1}{2})$となるから曲率円の中心は$O_1(0,\dfrac{1}{2})$となる。したがって曲率半径は$\dfrac{1}{2}$となる。よって$\dfrac{3}{5}>\dfrac{1}{2}$から$ ②$つまり曲率円の半径が重心の距離より小さくなることが成り立つため原点では不安定なつりあいとなる。
図$3’$

安定なつりあいの点

原点が接点の時は不安定なつりあいとわかったが、他に安定なつりあいの点はないのだろうか。この物体は$y$軸対称だから$t>0$として力(のモーメント)がつりあう接点を$T(t,t^2)$とおく。$T$における法線$y=-\dfrac{1}{2t}x+t^2+\dfrac{1}{2}$上に$G$があるため$\dfrac{3}{5}=-\dfrac{1}{2t}\cdot0+t^2+\dfrac{1}{2}$となる。(図$4$)
これを解くと$t=\dfrac{1}{\sqrt{10}}$であり、この点が不安定なつりあいか安定なつりあいかどうかを調べる。
$T$における曲率円の中心を$O_2$とおくと、$T$における法線つまり$y=-\dfrac{\sqrt{10}}{2}x+\dfrac{3}{5}$と$P(p,p^2)(p\ne\dfrac{1}{\sqrt{10}})$における法線の交点を$(m,n)$とおくと$n=-\dfrac{\sqrt{10}}{2}m+\dfrac{3}{5}$,$n=-\dfrac{1}{2p}m+p^2+\dfrac{1}{2}$である。
これを解くと$m=-\dfrac{2p(\sqrt{10}p+1)}{10},n=p(p+\dfrac{1}{\sqrt{10}})+\dfrac{3}{5}$で、$p→\dfrac{1}{\sqrt{10}}$のとき$m→-\dfrac{\sqrt{10}}{25},n→\dfrac{4}{5}$となるから$O_2(-\dfrac{\sqrt{10}}{25},\dfrac{4}{5})$と求まる。$TO_2$が曲率円の半径となるが,$m<0$より図$\small4$から$TO_2>TG$となり、曲率円の半径が重心の距離より大きい。したがって$T(\dfrac{1}{\sqrt{10}},\dfrac{1}{10})$は安定なつりあいとなる。
図$4$
図$4’$

まとめと考察

この図形を床においた時、$O$が床との接点となった時は不安定なつりあいで(図$5$)、$T$が接点となったときは安定なつりあいである(図$6$)。
図$5$
図$6$
また、中心$G$の円を半径を変えていくとき、放物線との接点で半径で大きい方が$O$で、小さい方が$T$となる(図$\small7$)。このことから重心が低い位置にあるほど位置エネルギーが小さいため安定しやすいと考察できる。しかし、半径はそれぞれ$\dfrac{3}{5}$と$\dfrac{1}{2}\sqrt{\dfrac{7}{5}}$であり、差は約$0.0084$しかない。
図$7$
図$7’$

一般化

一般化すると次のようなことがわかる。以下の問いに答えよ。
$(1)\space$$y=x^2$と$y=k(k>0)$で囲まれる一様な物体は、放物線側を下にしたときについて、$0< k<α$のとき、原点のみで安定なつりあいをする。$k=α$のとき、原点のみで中立なつりあいをする。$k>α$のとき、原点で不安定なつりあいをし、$y$軸で対称な二点で安定なつりあいをする。このとき、$α$を求め、$k>α$のときの$y$軸で対称な安定なつりあいをする二点を$k$を用いて表せ。
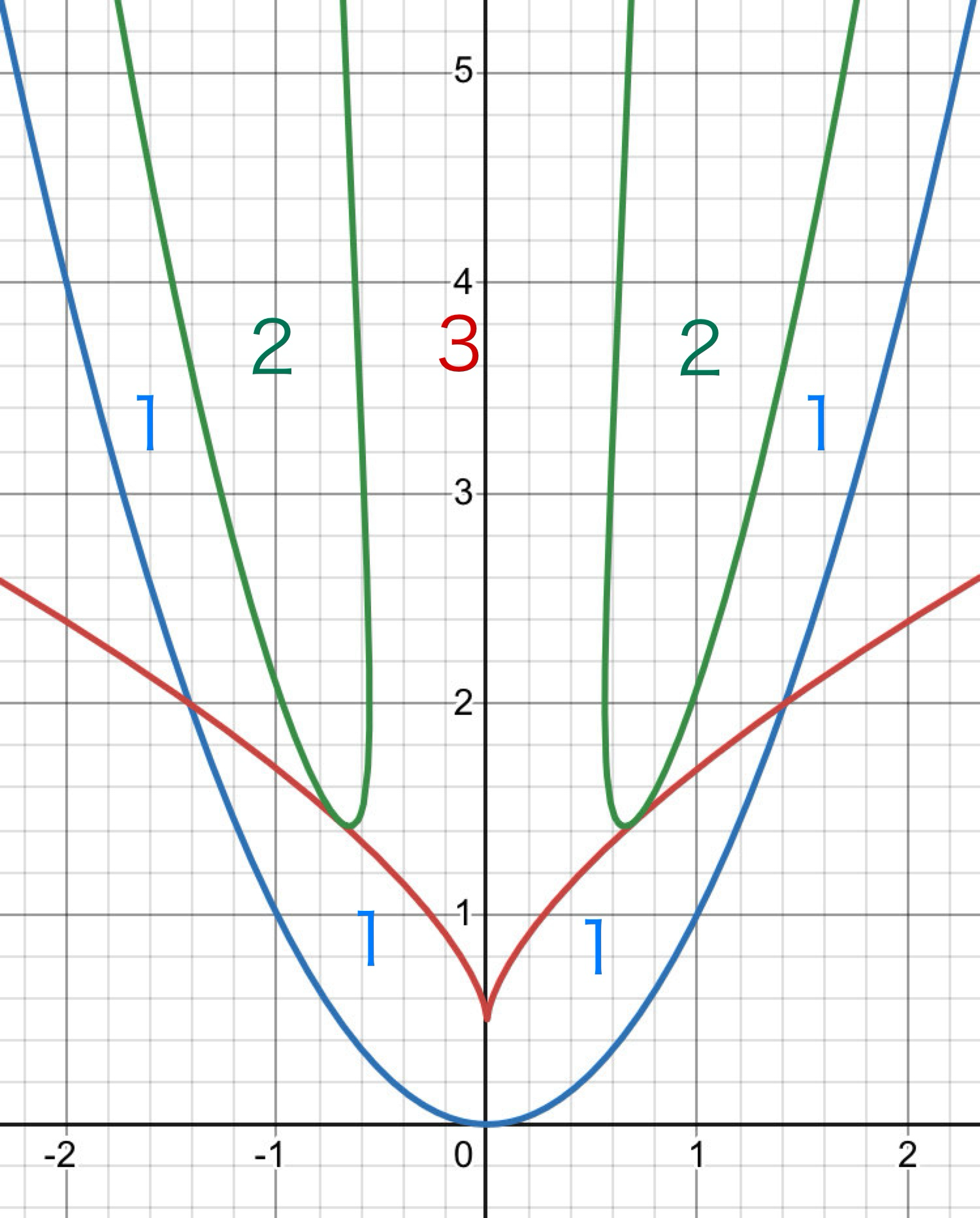
$(2)\space$$y=a’x^2+b’x+c’$と$y=d’x+e’\space$$(a’>0,(b’-d’)^2-4a’(c’-e’)>0)$で囲まれる物体のつりあいは、適切に平行移動、拡大縮小をすることで、$y=x^2$と$y=ax+b\space(a^2+4b>0)$で囲まれる物体と相似となり、この物体のつりあいを考えればよいから、以下この物体について考える。このとき、重心の座標を選べば、直線の式が定まり、つりあいの個数は$1$個、$2$個、$3$個のいずれかである。つりあいの個数は$1$個、$2$個、$3$個である物体の重心の領域を図示すると境界線として、ある曲線が現れ、以下のようになる。このとき、境界となる曲線の方程式および緑の曲線と赤の曲線の接点を求めよ。
重心