自己紹介とデザルグの定理

自己紹介

はじめまして。りらひいと申します。
趣味で少し数学をしているおじさんです。
会社の食堂兼休憩室で始業前や休憩時間によく計算をしています。
紙とペンがあればできるのが数学のいいところですね。

わたしはデザルグの定理が好きなので、プロフィール画像はその配置にしてみました。
この図形について少し書きたいと思います。

デザルグの定理における点と直線の配置

デザルグの定理は次のような定理です。

デザルグの定理は射影幾何の定理なのでユークリッド平面の場合は多少の修正が必要になりますが、この記事では説明を省略します。
①②が成り立つとき$\triangle ABC$と$\triangle A'B'C'$は配景的であるといい、①で定まる点を配景の中心、②で定まる直線を配景の軸といいます。

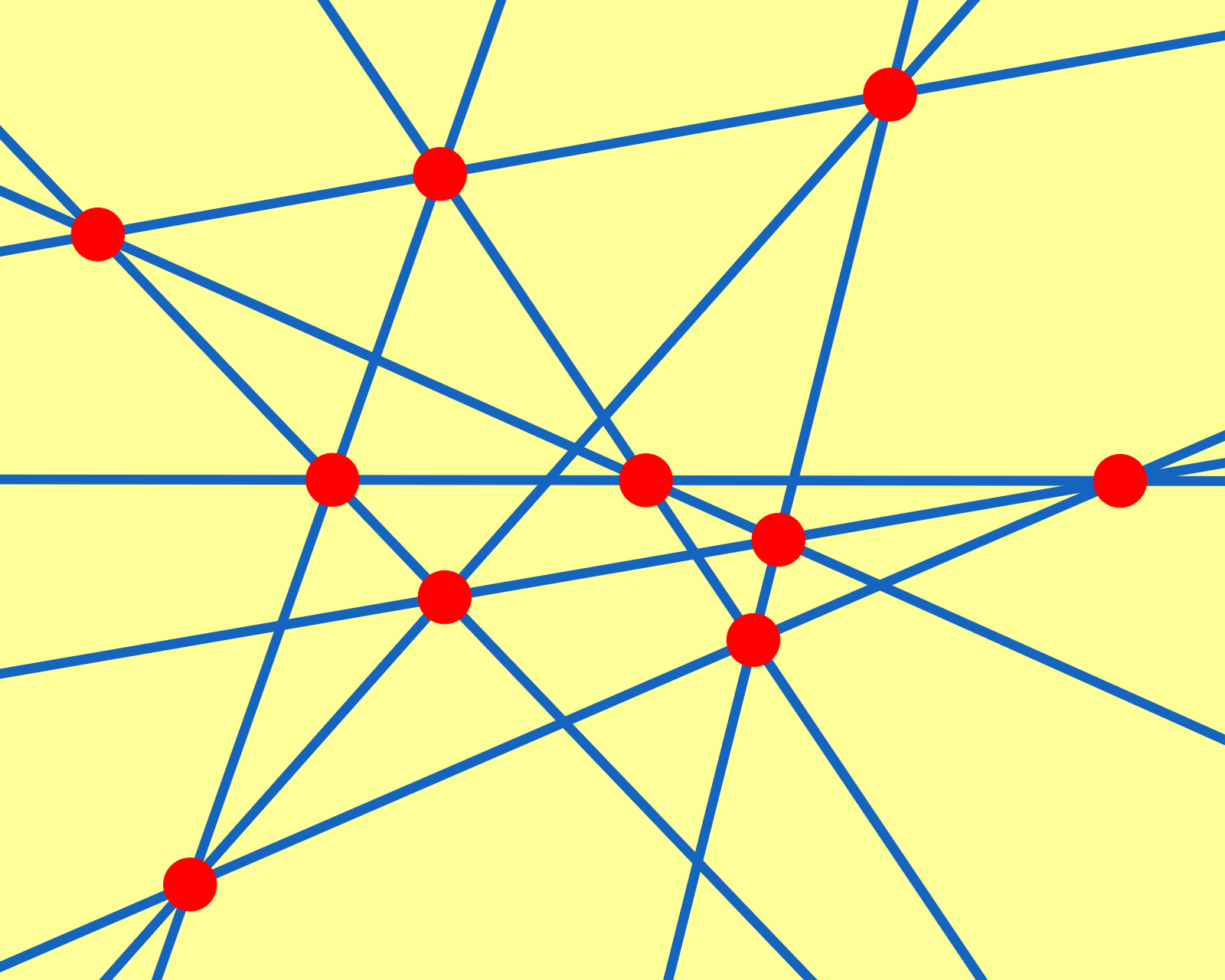
プロフィール画像に使ったのは次のような図です。
Desargues configuration
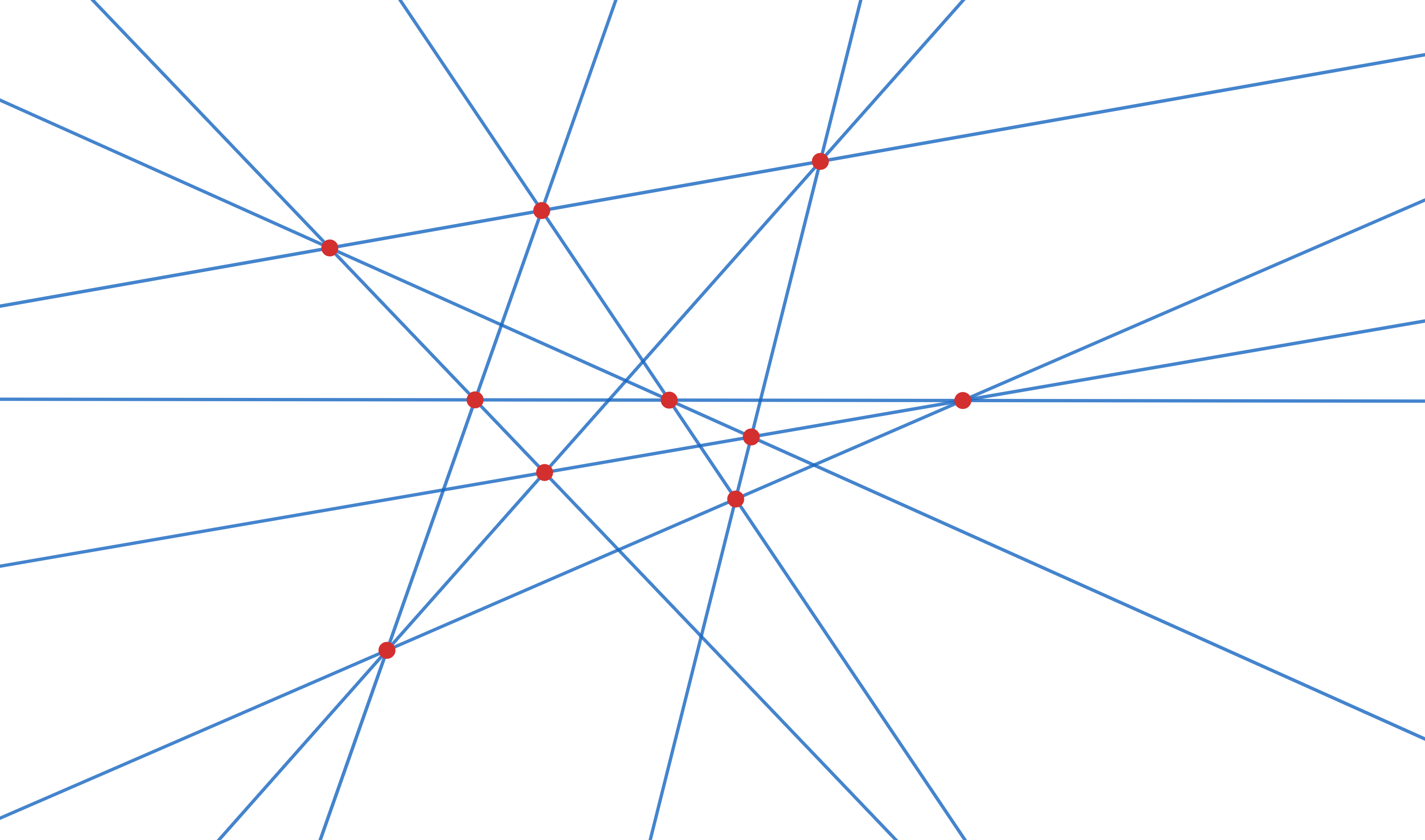
これを見ると、赤点が10個と青線が10本あります。
さらによく見ると、各赤点をちょうど3本の青線が通り、各青線の上にちょうど3個の赤点があります。
さらにさらによく調べると、赤点を頂点とし青線を辺とする三角形が20個あることがわかります。

実はこの図には「配景的な2つの三角形とその配景の中心と配景の軸」のセットが10通り潜んでいます。
見つけられますか？

以下にその10パターンを図示します。
ちょっとわかりにくいですが、点や直線の位置は変えていません。色やスタイルだけ変えています。

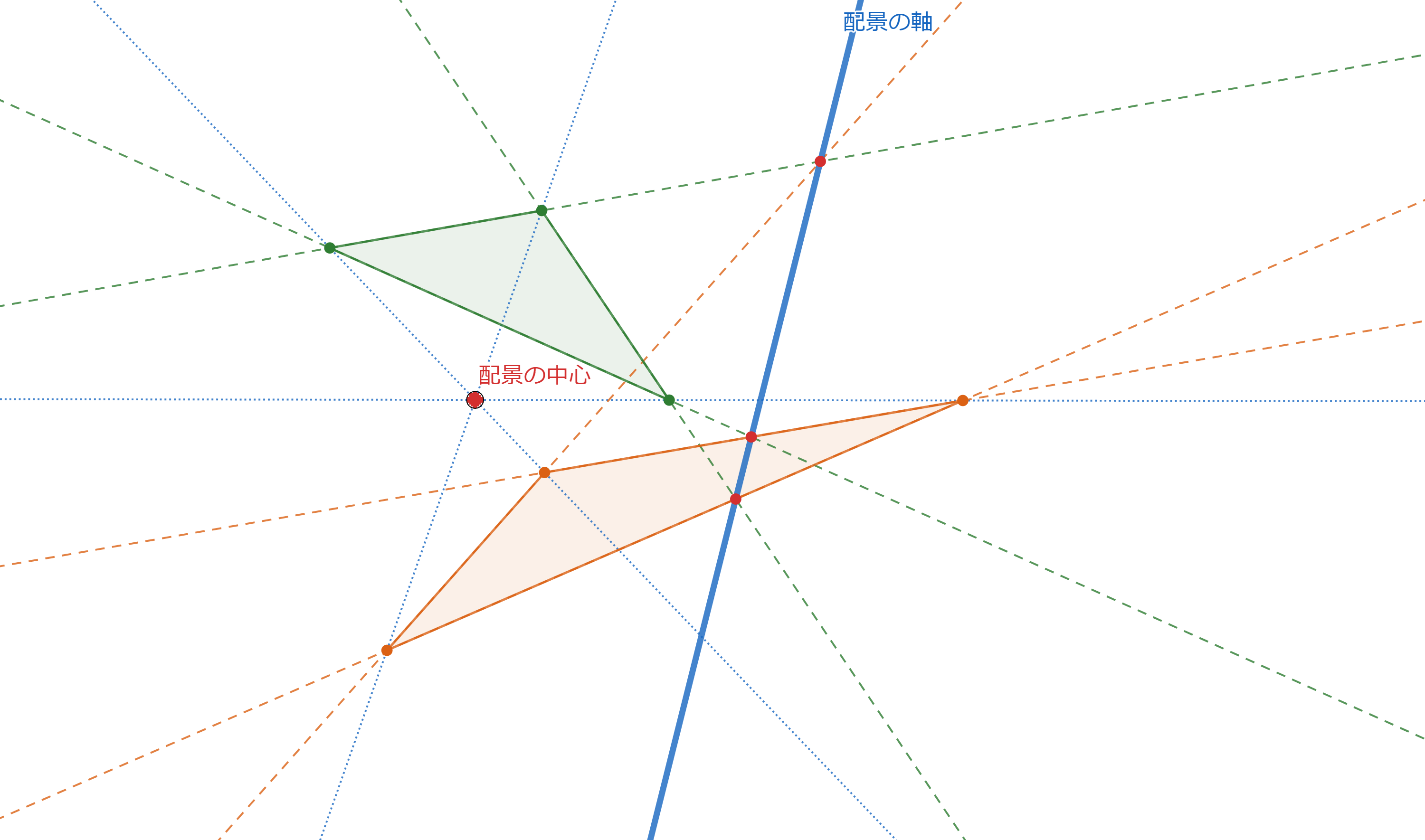
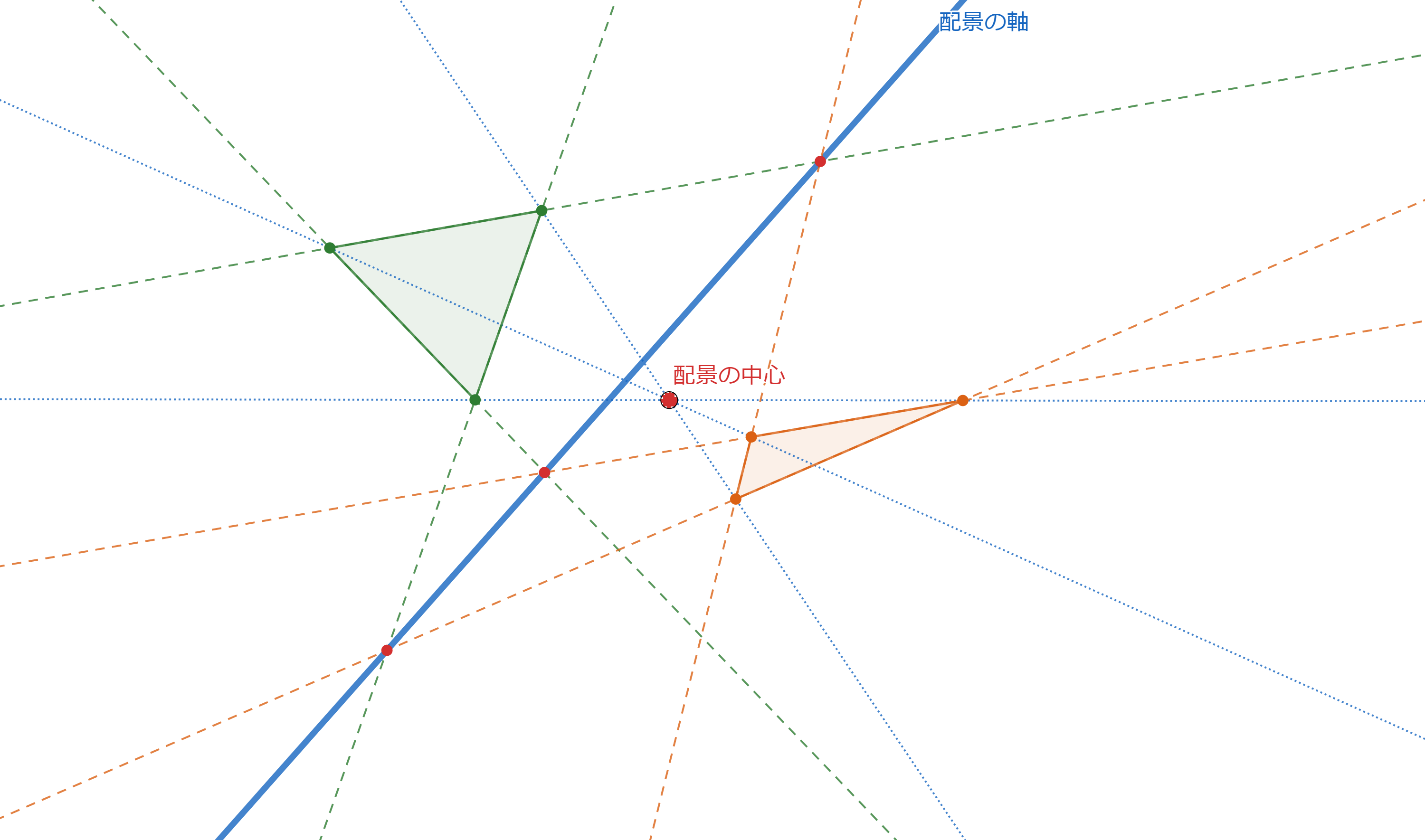
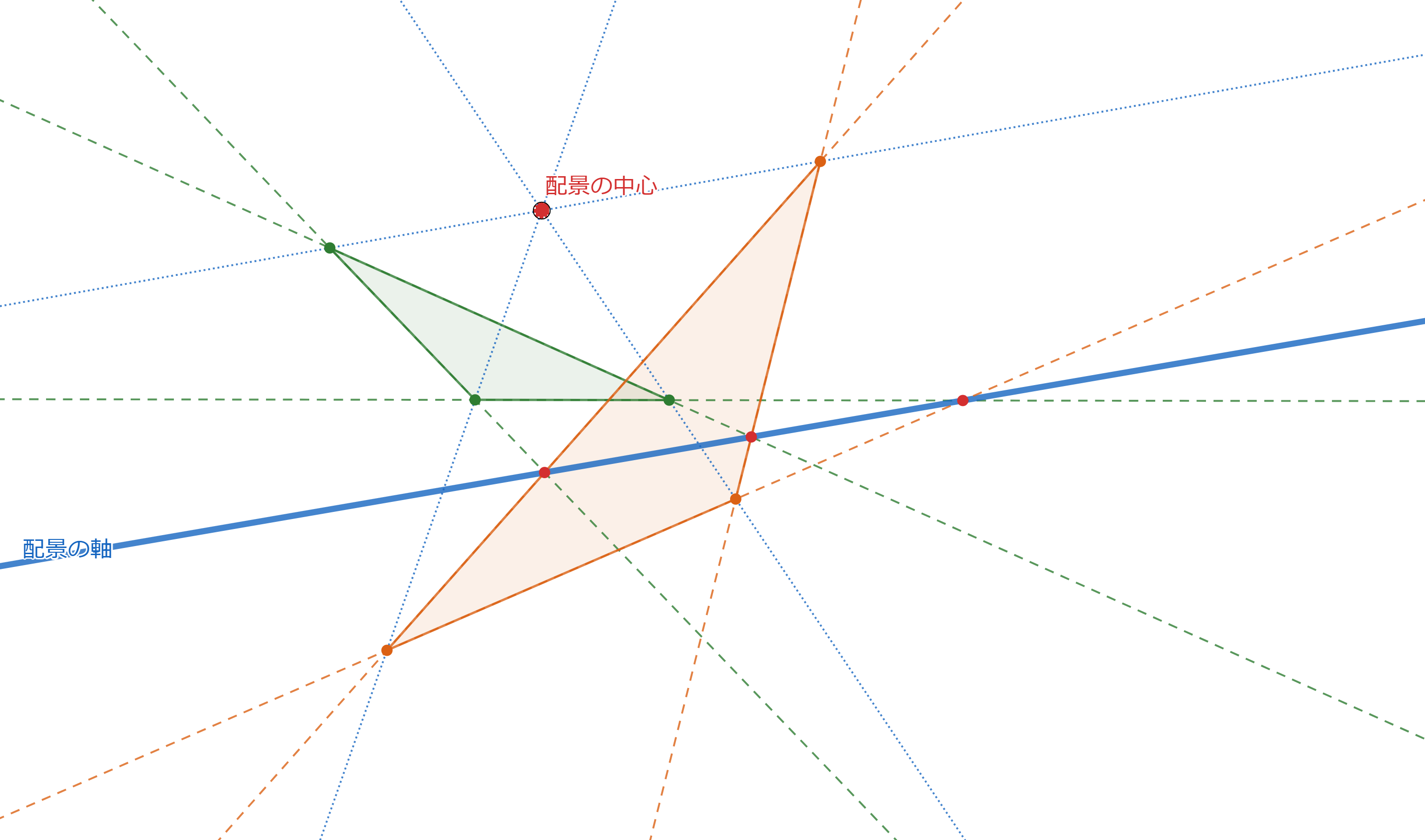
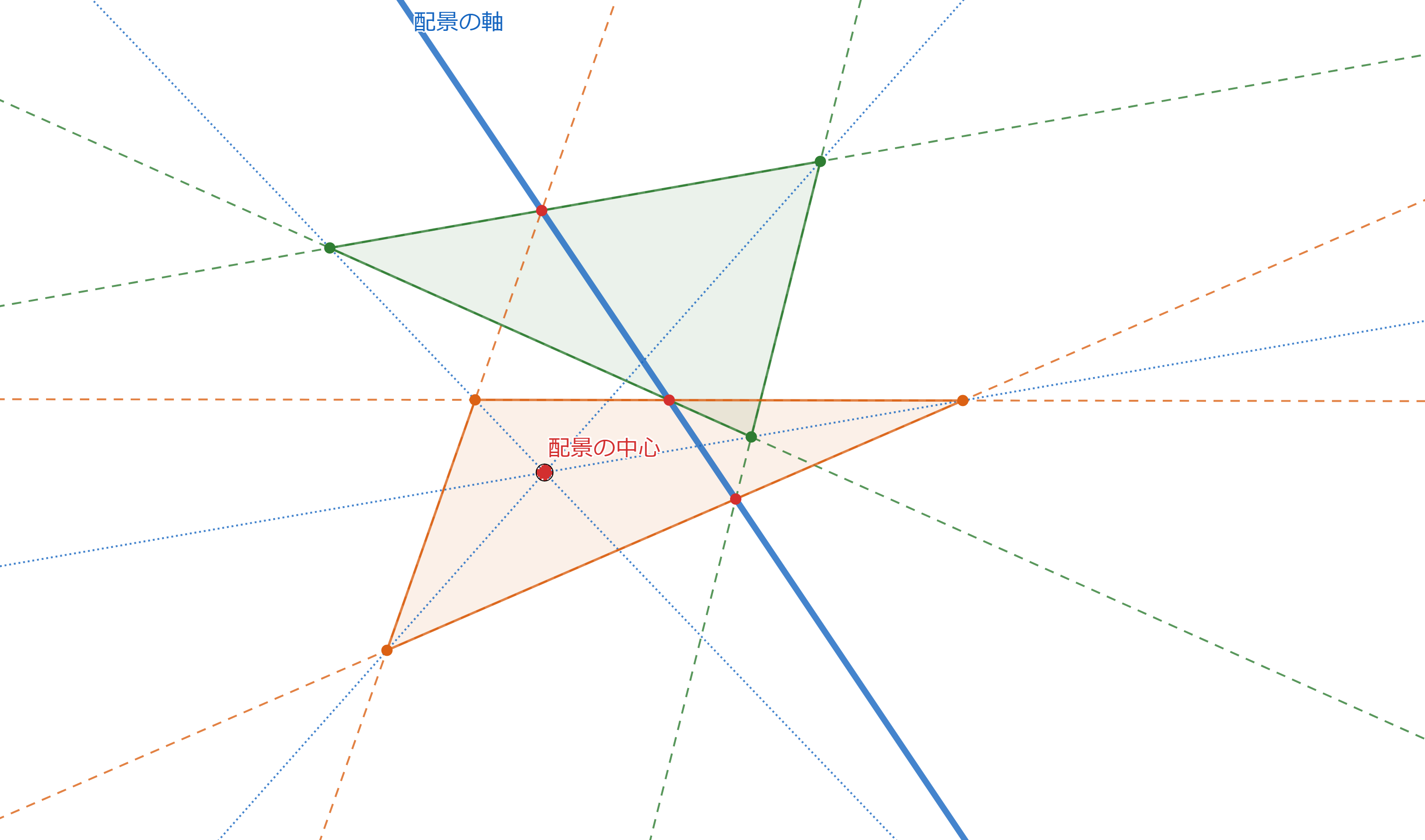
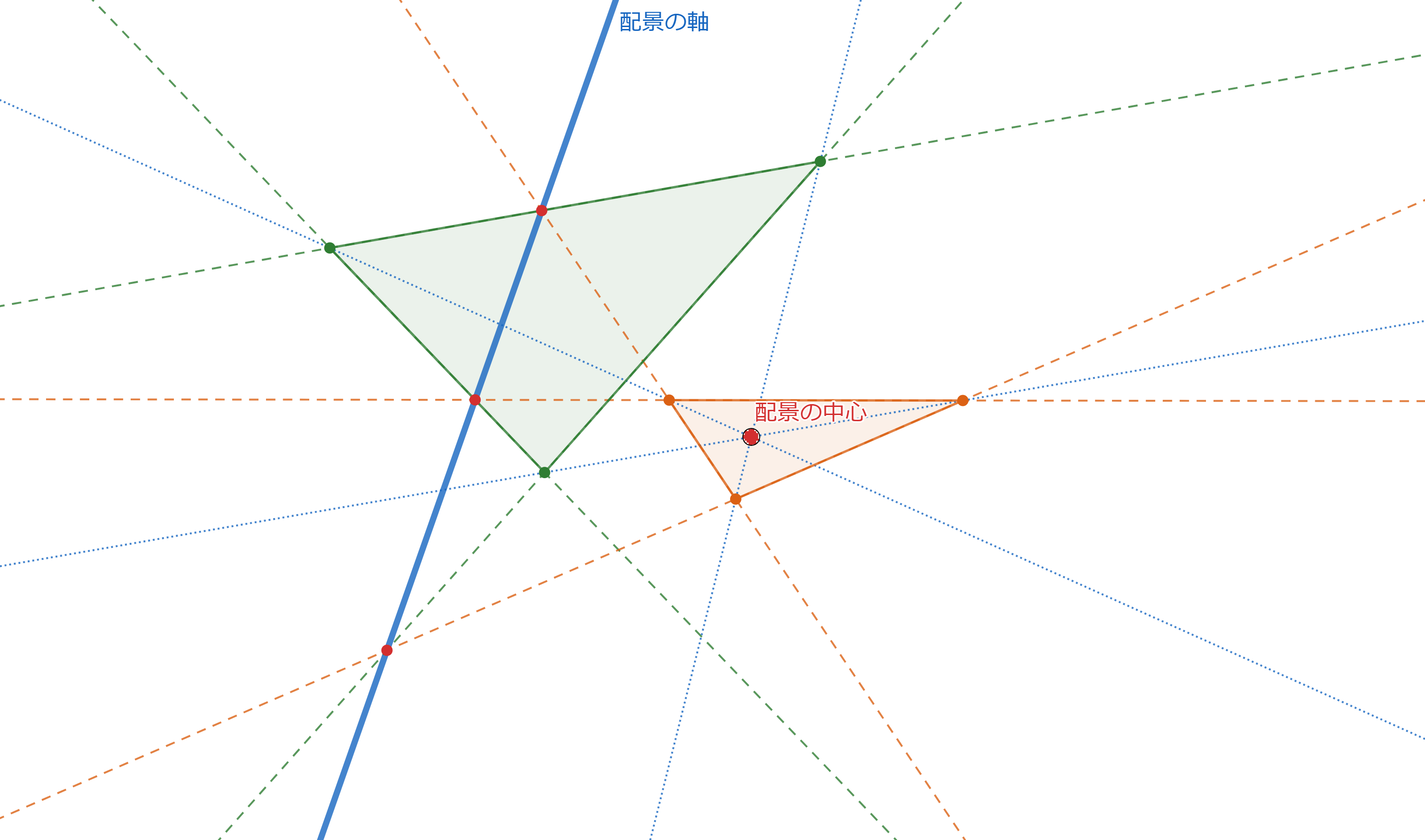
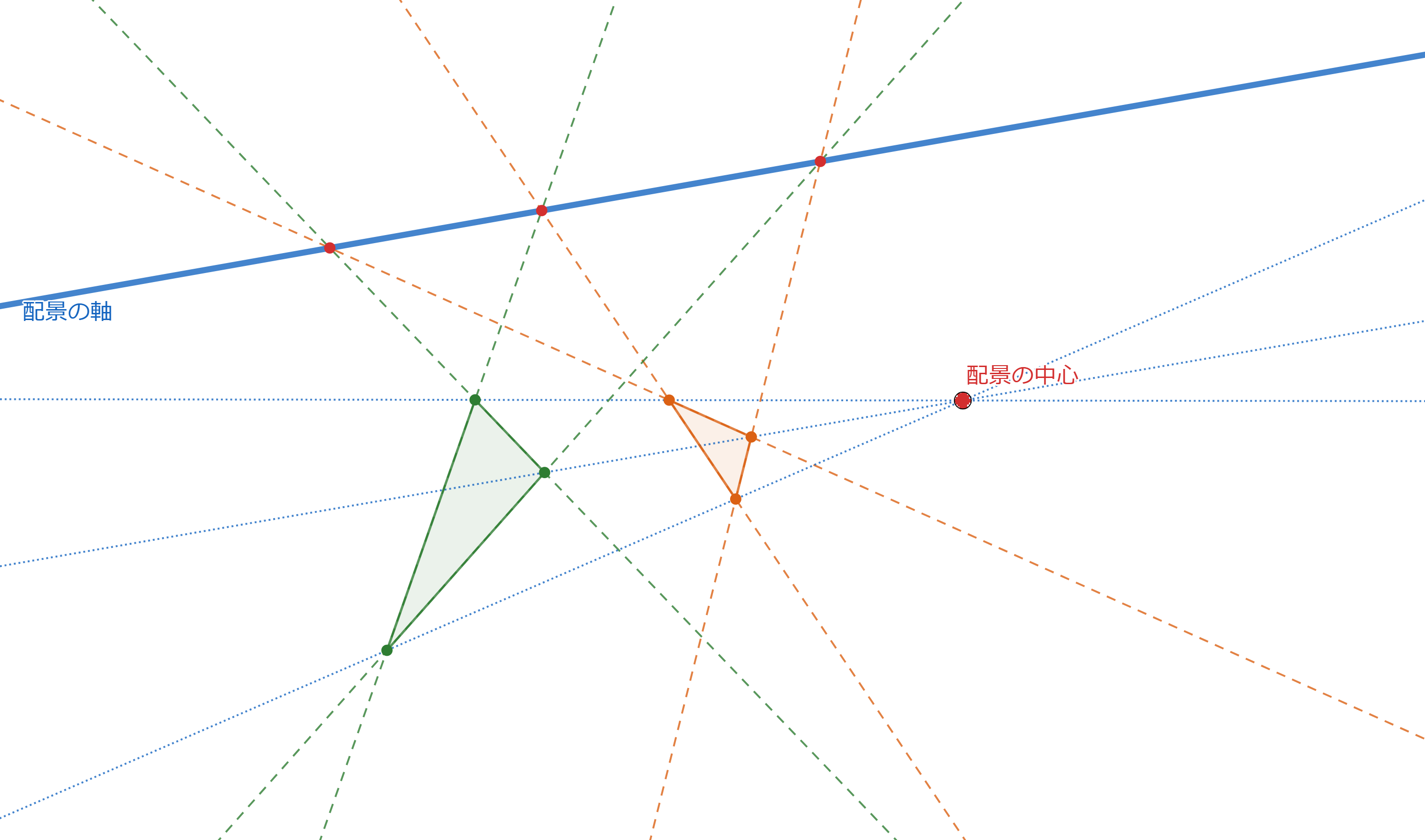
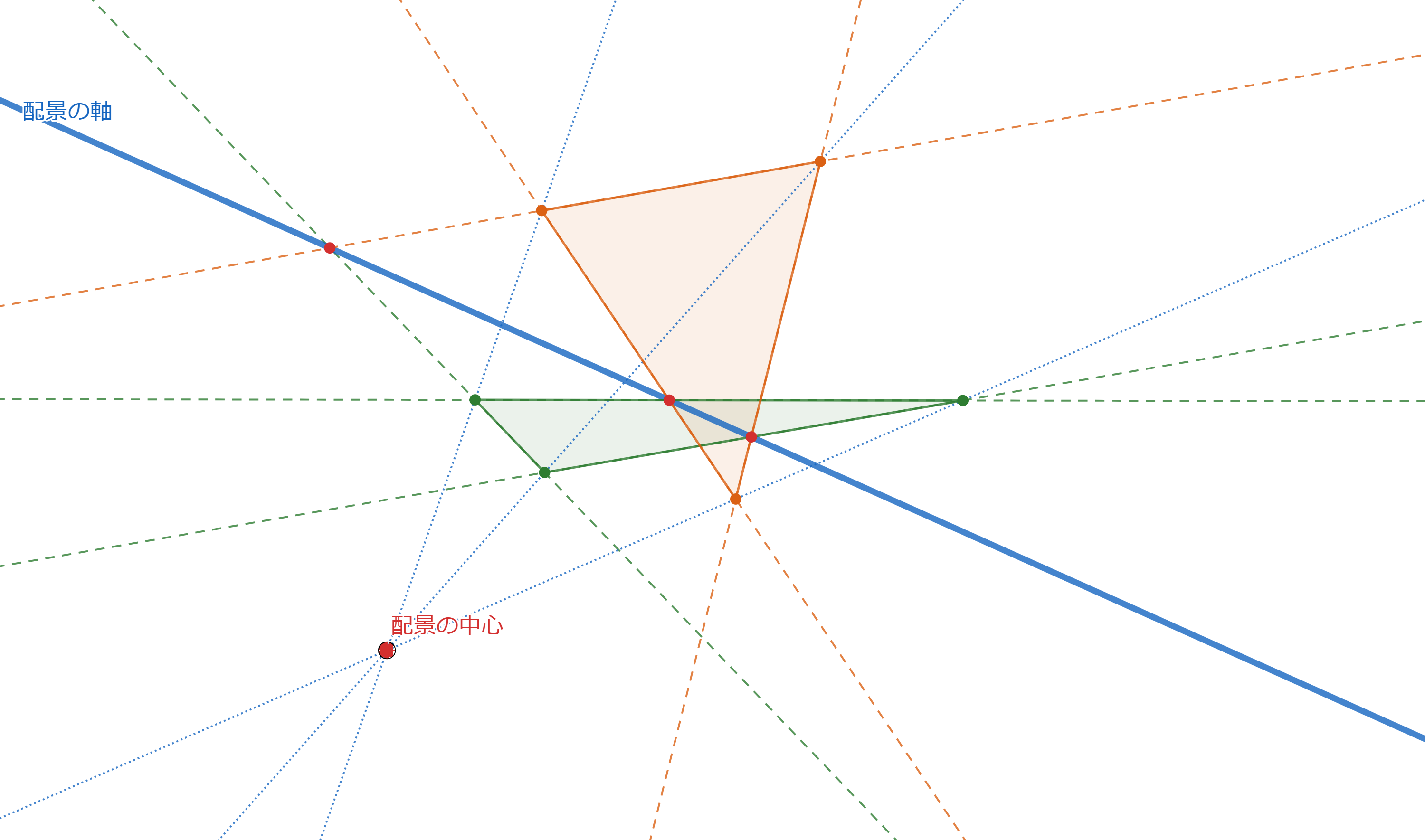
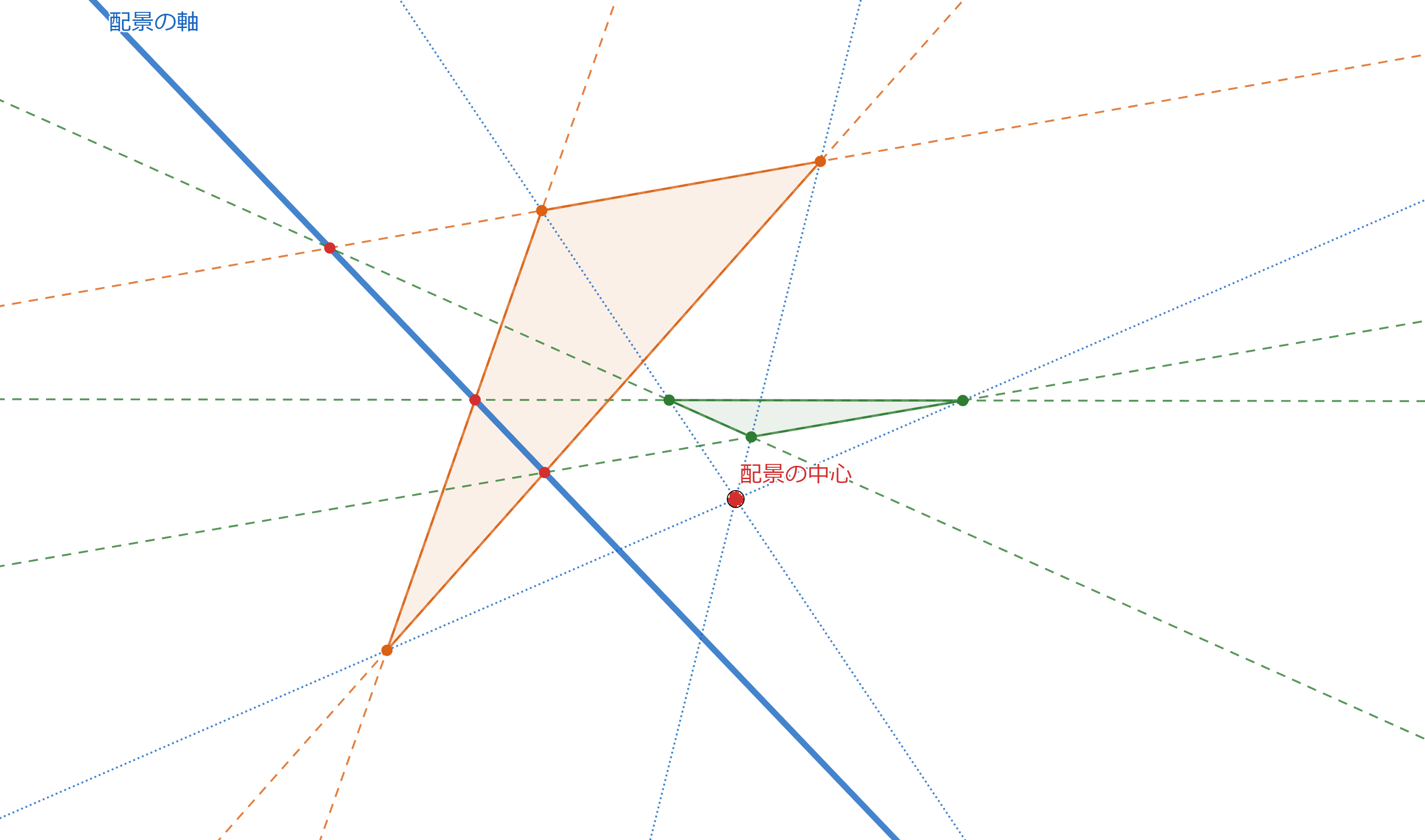
どの赤点も配景の中心になり、どの青線も配景の軸になります。また、20個の三角形も一回ずつ現れます。
対称性が高くてとても美しいとわたしは思います。

これから

最近わたしは三角形幾何の座標計算をいろいろしているので、今後それについての記事を書いていきたいと思っています。ただ、時間があまりとれないので書き上げるのはまだまだ先になりそうです。