【ひらめき!】三平方の定理の証明方法を知ろう【画像で解説】
三平方の定理ってなんだっけ?
三平方の定理(ピタゴラスの定理)をご存知でしょうか?$a^2 + b^2 = c^2$の式を一度は見たことがあると思います。三平方の定理は「直角三角形の2辺の長さが分かれば、もう1辺の長さも分かる」というもので、色々な場面で使うことになります。
この記事ではたくさんの画像を使用して三平方の定理の証明方法をお伝えします。ぜひ一緒にマスターしていきましょう!
三平方の定理とは
まずは、三平方の定理を確認してみましょう。
直角三角形において、直角と接する2辺を$a,b$その他の辺を$c$とした時に
$$a^2 + b^2 = c^2$$
が成り立つ。
こんな図形を想像できますね。
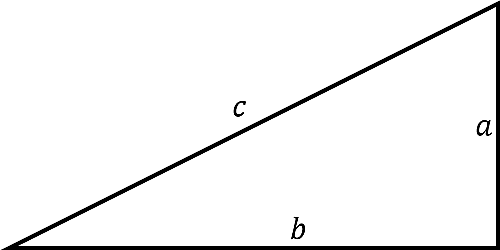
ここまでは大丈夫でしょうか?
では、実際に証明をしてみましょう。
三平方の定理の証明
まずは上の直角三角形を参考にして、直角三角形の直角と接する2辺$a,b$を用いた2つの正方形と、その2つの正方形を利用したもう一つの直角三角形を作ってみましょう。
以下の図のようになります。

次に、2つの正方形を利用して、もう一つの直角三角形を作ってみましょう。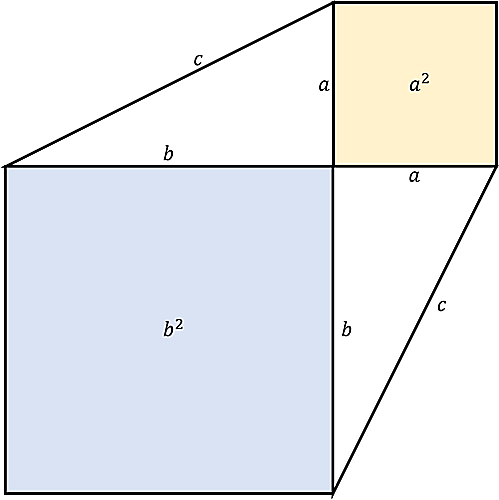
さて、これで$a^2$と$b^2$ができました。
では、ここからどのように$c^2$を生み出して証明するのでしょうか?
少しだけ考えてみましょう。
...。
...。
...。
わかりましたか?
では、一気に見ていきましょう!
まず、2つの正方形を通る対角線でこの図形を真っ二つにします。

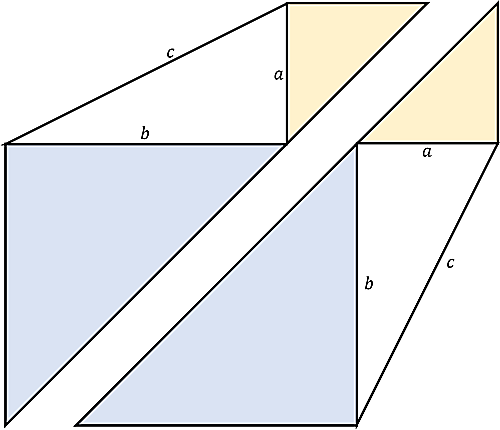
そして片方をひっくり返します。
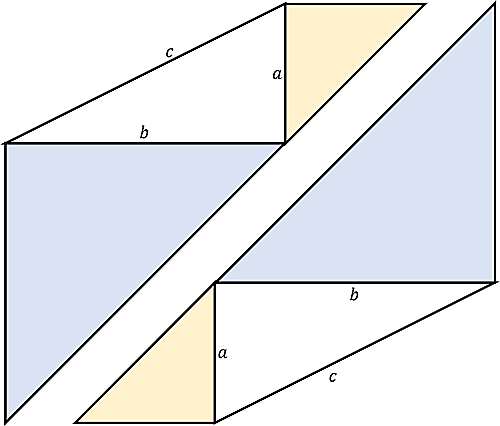

さて、この図形を見てお気づきの方はいらっしゃいますか??
もう少しだけ情報を足します!

もうお気づきでしょうか?
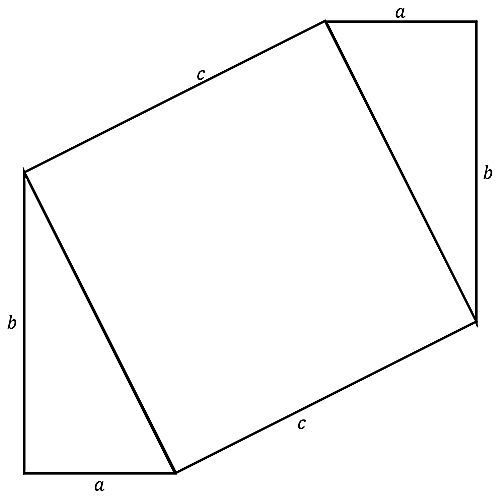
こうして、
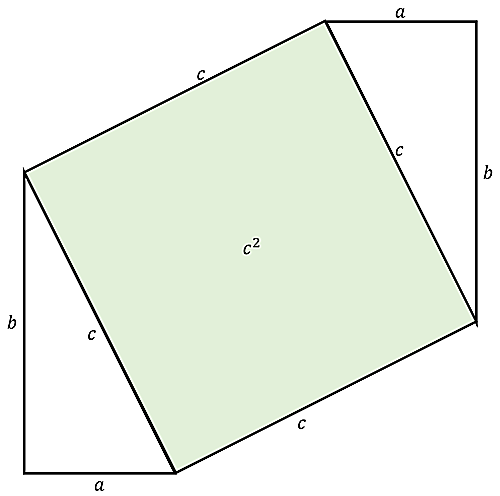
こうです!
なんと、$c^2$が現れました!
ここで、2つの図形の面積を比べてみましょう。
1つ目の図形の面積は$a^2 + b^2 + ( a \times b )$です。
2つ目の図形の面積は$c^2 + ( a \times b )$です。
$( a \times b )$は直角三角形2つの面積を計算すると出てきます。
$( ( a \times b )\div 2) \times 2 = a \times b $
2つの面積は等しいため、$a^2 + b^2 + ( a \times b ) = c^2 + ( a \times b )$
$(a \times b)$はキャンセルされるため、$a^2 + b^2 = c^2$
はい!証明できました!!
まとめ
三平方の定理の証明で大事なのは2つです。
- 正方形2つと直角三角形2つの図形を作る
- 半分にして片方をひっくり返す
これさえ忘れなければ大丈夫。
余談
今回の証明方法はレオナルドダヴィンチさん考案の方法です。
実は、三平方の定理の証明方法は100種類以上あります。
それらがギュッとまとまった書籍があるので、以下にリンクを記載しておきますね。
今回紹介した証明よりカッコイイ証明があるかも?
興味がある方はぜひチェックしてみてください!
ピタゴラスの定理 100の証明法―幾何の散歩道 森下 四郎
ではでは、おつかれさまでした!
