

&&&exc 
正方形$ABCD$の中に正三角形$EFG$が入っている。$AE=2 \sqrt{3}$ $DG=7$の時$AF$を求めよ。
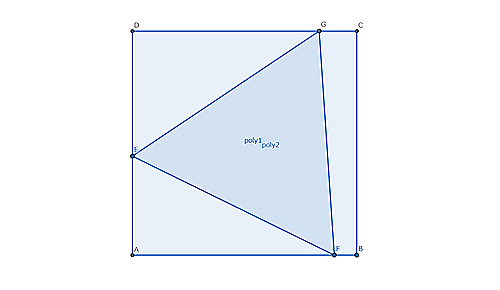![sss](/uploads/mathdown/20201122172017.jpg)
&&&
$ $
$ $ 
$ $
$ $
$ $
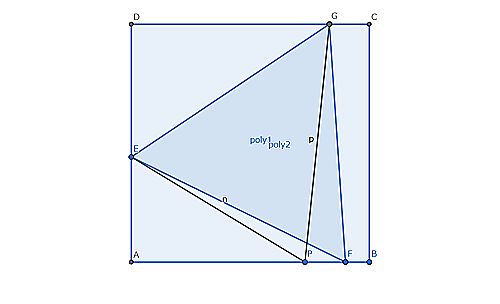
$PG=GF$となるように$AB$上に点$P$を取る。
この時、$\triangle EPF$の外心は点$G$なので、$\angle EPA=30^{\circ}$
$AE:AP=1:\sqrt{3}$より$AP=6$
$PG=GF$より、
$DG-AP=AF-DG$
$7-6=AF-7$
$AF=8$
![ppp](/uploads/mathdown/20201122172724.jpg)



正方形の中に正三角形が入っている時だけ使えるテクニック

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント