0は何桁の整数？

子供の頃に思った疑問です。
以前、Twitterで$0$,$1$,$-\infty$,その他の投票形式でツイートしたところ、 こんな結果になりました。
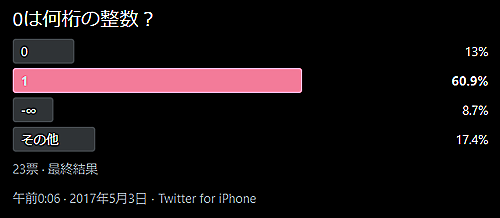0の桁数の投票結果

• $0$派の意見
  $1\underbrace{000\cdots 000}_{n-1}$が$n$桁の整数であり、これより$1$小さいと$n−1$桁になる。
  $n=1$の場合を考えると$0$は$0$桁になる。

• $1$派の意見
  整数の桁数を「数字の個数(文字列の長さ)」と考えると、$0$は$1$文字だから$1$桁になる。
  ($0.5$は$3$文字だから$3$桁という過激派(？)もいました...)

• $-\infty$派の意見
  $n$の桁数を$\lfloor\log_{10}(n)+1\rfloor$と考えると、$0$は$−\infty$になる。

• その他派の意見
  桁数はそもそも正の整数のみに定義されているのでは？
  ・・・うん。自分もそう思う。
  だけど、なんだかんだ言って数学では$−\infty$とすると便利なことが多そうな気がしなくもない・・・

$1$が多いのは個人的には意外でした。割と文字数で考える人は多いようです。

以上、読んでいただきありがとうございます。