斜めの放物線

中学生の頃, 放物線 $y=ax^2$ を時計回りに $90$ 度だけ傾けたグラフを表す方程式は何かと考え, すぐに $x=ay^2$ だと気付きました.
しかし, $90$ 度ではない回転をした場合の方程式については, 難しすぎて予想を立てるのみとなりました.
中学生の私は, 自宅近くの文房具屋でマスの細かい方眼紙を買ってきて, 何度も書いて実験し, 次のようだと判断しました.

この予想が正しいことを高校数学の範囲内で証明するのが今回のお題です.

まずは頂点が原点の場合を考え, それを回転させた後で平行移動をすることにします.
放物線 C:$y=ax^2$ ($a \neq 0$) 上の点 $(x,y)$ を原点を中心として $\theta$ だけ回転した点を $(X,Y)$ とします.
ここで, $-\frac{\pi}{2} < \theta < 0$, $0 < \theta < \frac{\pi}{2}$ ... (1) と仮定します.
このようにしても一般性を失いません.
実際, $\frac{\pi}{2}$ の整数倍の回転では軸が $x$ 軸または $y$ 軸に垂直になりますし, 放物線 C を (1) の範囲で回転させた各々は, 放物線 $y=-ax^2$ を (1) の範囲で回転させた各々に一対一に対応するからです.

加法定理や複素数平面や行列 (今は高校数学の範囲外) など, 何でもいいですが, それらの知識を使って $(x,y)$ と $(X,Y)$ の関係式を求めると
$X=x \cos \theta-y \sin \theta$,
$Y=x \sin \theta+y \cos \theta$
となることが分かります.
今後, 面倒なので, $s=\sin \theta$, $c=\cos \theta$ とおきます.
$x=cX+sY$,
$y=-sX+cY$
となることが分かるので, これを放物線 C の方程式に代入して整理すると
$as^2Y^2+c(2asX-1)Y+ac^2X^2+sX=0$.
仮定より $as \neq 0$ なので, 解の公式と, $s^2+c^2=1$ であることにより
$\displaystyle Y=-\frac{c}{s}X+\frac{c}{2as^2}\pm\sqrt{-\frac{1}{as^3}+\frac{c^2}{4a^2s^4}}$.
この放物線を, $x$ 軸方向に $p$, $y$ 軸方向に $q$ だけ平行移動すると
$\displaystyle Y=-\frac{c}{s}X+\frac{c}{2as^2}+\frac{c}{s}p+q\pm\sqrt{-\frac{1}{as^3}X+\frac{p}{as^3}+\frac{c^2}{4a^2s^4}}$ ... (2)
仮定より $asc \neq 0$ なので, 各項の分母が $0$ になることはなく, $X$ の係数がいずれも $0$ でないことが分かります.

以上により, 斜めの放物線の方程式は
$Y=AX+B\pm\sqrt{CX+D}$ (ただし, $AC \neq 0$) ... (3)
の形で表されることが分かりました.
(大文字を小文字に直せば公式 1 の式になりますね.)

次は, (3) の形が任意に与えられたとき, それがただ一つの斜めの放物線を表すことを確認します.
(2) と (3) を見比べると, 次のようになります.
$\displaystyle A=-\frac{c}{s}$ ... (4)
$\displaystyle B=\frac{c}{2as^2}+\frac{c}{s}p+q$ ... (5)
$\displaystyle C=-\frac{1}{as^3}$ ... (6)
$\displaystyle D=\frac{p}{as^3}+\frac{c^2}{4a^2s^4}$ ... (7)
ここで, $\displaystyle \frac{c}{s}=\frac{1}{\tan \theta}$ であることに注意すると, (4) により $A$ から $\tan \theta$ が定まり, したがって $s$ および $c$ も定まります.
すると, (6) により, $C$, $s$ から $a$ が定まります.
次に, (7) により, $D$, $s$, $c$, $a$ から $p$ が定まります.
最後に, (5) により, $B$, $s$, $c$, $a$, $p$ から $q$ が定まります.
したがって, (3) の形は確かにただ一つの斜めの放物線を表すことが分かります.

Q.E.D.

試しに $y=x+2\pm\sqrt{3x+4}$ のグラフを描いてみました.
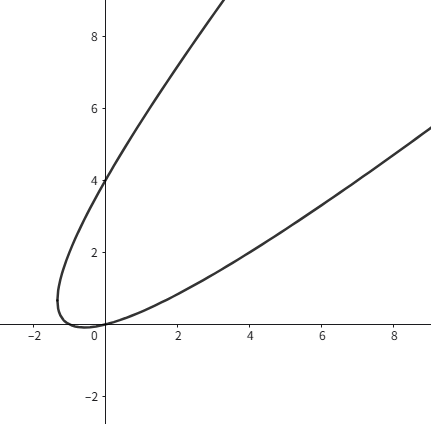斜めの放物線