三角関数の中身のずらし方_備忘録
はじめに
なんとなく、まとめてみたい気分になったので。
$\sin (\pm x \pm \frac{k\pi}{2})$、$\cos (\pm x \pm \frac{k\pi}{2})$公式の覚え方
虚数単位$i$の累乗と対応づけて覚える方法がある。
下の表は微分でも同じ並びが出てくるので、覚えておくと良いかも。
$\sin x$、$\cos x$のグラフから値を追うことで判断する方法もあり。
加法定理から導くこともできるが、正確に短時間で判断できることが望ましい。
| $k$ | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| $i^k$ | $1$ | $i$ | $-1$ | $-i$ | $1$ | $i$ |
| $\sin (x+\frac{k \pi}{2})$ | $\sin x$ | $\cos x$ | $-\sin x$ | $-\cos x$ | $\sin x$ | $\cos x$ |
| $k$ | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| $i^{-k}$ | 1 | $-i$ | $-1$ | $i$ | $1$ | $-i$ |
| $\cos (x+\frac{k \pi}{2})$ | $\cos x$ | $-\sin x$ | $-\cos x$ | $\sin x$ | $\cos x$ | $-\sin x$ |
求めたいのは$\sin x$、$-\sin x$、$\cos x$、$-\cos x$のどれかなので、
下図のように判断することも可能。
ズレが$2\pi$以上あったり、変数に$-$がついているときは最初にそれを処理するのが良さそう。
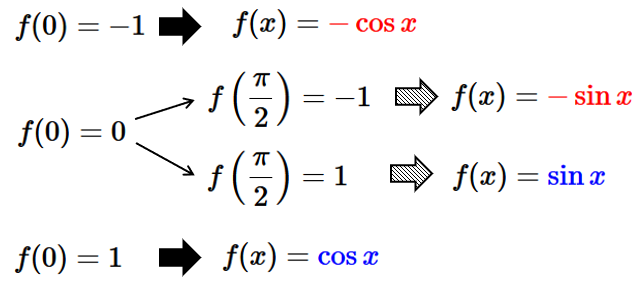
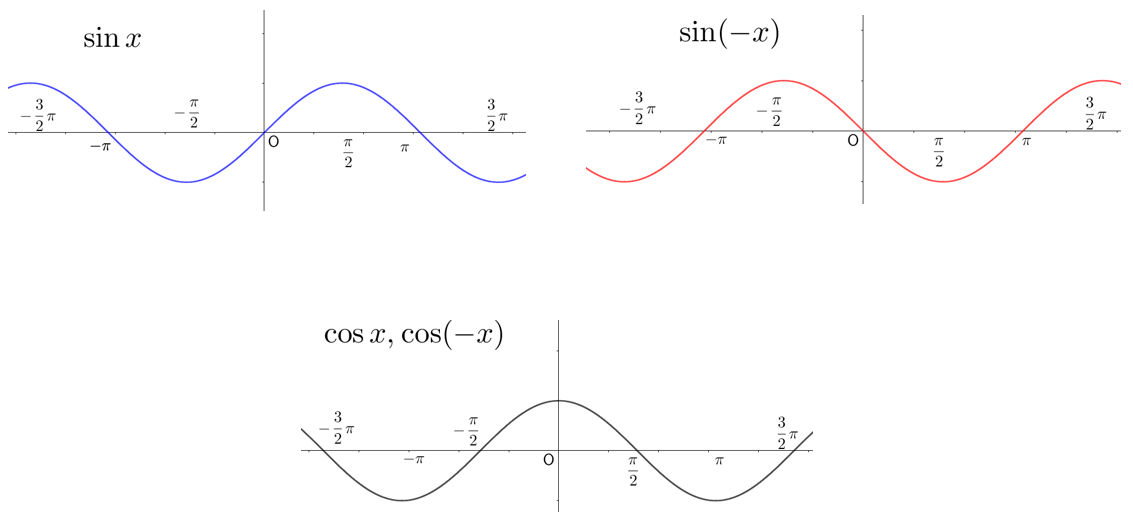
脳内でグラフを描くための手がかりとして、
$\sin x$のグラフ→原点の右側に山がある。
$-\sin x$のグラフ→原点の左側に山がある。
$\cos x$のグラフ→原点の位置に山がある。
手順
$\sin (\pm \alpha \pm \frac{k\pi}{2})$、$\cos (\pm \alpha \pm \frac{k\pi}{2})$の形の三角関数を簡単にする手順をまとめておきます。
三角関数のグラフを$-\pi \leq x \leq \pi$の範囲でイメージできればいける感じ。
最初に、以下のように記号を定める。
カッコ内の変数$\alpha$の符号:$\mathrm{sgn}_{\mathrm{v}}$
カッコ内の定数の符号:$\mathrm{sgn}_{\mathrm{s}}$
カッコ内の定数の絶対値:$\mathrm{abs}$
- 参照するグラフを決める。
関数が$\cos$ → $y=\cos x$のグラフ
関数が$\sin$
$\mathrm{sgn}_{\mathrm{v}}=+1$ → $y=\sin x$のグラフ
$\mathrm{sgn}_{\mathrm{v}}=-1$ → $y=-\sin x$のグラフ
$\\[5px]$ - 参照すべきグラフの位置を決める。
$\mathrm{abs}$から適当に$2\pi$を引く
次のように$\mathrm{abs}$を変換する。変換に応じて新しい符号$\mathrm{sgn}_{\mathrm{t}}$を導入する
$$\mathrm{abs}=\frac{3}{2}\pi, \frac{7}{2}\pi \implies \mathrm{sgn}_{\mathrm{t}}=-1 ,\quad\mathrm{abs}'=\frac{1}{2}\pi$$
$$\mathrm{abs}=\frac{1}{2}\pi, \frac{5}{2}\pi, \frac{9}{2}\pi \implies \mathrm{sgn}_{\mathrm{t}}=1 ,\quad\mathrm{abs}'=\frac{1}{2}\pi$$
$$\mathrm{abs}=0, \pi \implies \mathrm{sgn}_{\mathrm{t}}=1, \quad\mathrm{abs}'=\mathrm{abs}$$
最終的に、次の$p$を考える。
$p=(\mathrm{sgn}_{\mathrm{v}} \cdot \mathrm{sgn}_{\mathrm{s}} \cdot \mathrm{sgn}_{\mathrm{t}}) \cdot \mathrm{abs}'$
$\\[5px]$ - グラフを参照し、$x=p$の周辺を観察する
山の頂点 → $\cos \alpha$
上り坂 → $\sin \alpha$
下り坂 → $-\sin \alpha$
谷底 → $-\cos \alpha$
参照するグラフの種類と参照位置、結果を表にするとこんな感じ
| $-\pi$ | $\displaystyle -\frac{\pi}{2}$ | $0$ | $\displaystyle \frac{\pi}{2}$ | $\pi$ | |
|---|---|---|---|---|---|
| $\sin$ | ${\color{red}-\sin}$ | ${\color{red}-\cos}$ | ${\color{blue}\sin}$ | ${\color{blue}\cos}$ | ${\color{red}-\sin}$ |
| $-\sin$ | ${\color{blue}\sin}$ | ${\color{blue}\cos}$ | ${\color{red}-\sin}$ | ${\color{red}-\cos}$ | ${\color{blue}\sin}$ |
| $\cos$ | ${\color{red}-\cos}$ | ${\color{blue}\sin}$ | ${\color{blue}\cos}$ | ${\color{red}-\sin}$ | ${\color{red}-\cos}$ |
例題
$$(1)\sin(-\theta+\pi)$$
$$(2)\sin(-\frac{7}{2}\pi-\alpha)$$
解答
定数部分が$\pi$の整数倍のときは
「$-\sin$(参照グラフ)の$1$($\mathrm{abs}$) → $\sin$」⇒$\sin(\theta)$
定数部分が$\frac{\pi}{2}$の奇数倍のときは
「$-\sin$(参照グラフ)の$-$($\mathrm{sgn}_p$) → $\cos$」⇒$\cos(\alpha)$
みたいに唱えながら解けば、そのうち慣れる気がする。
微分・積分のはなし
$\sin(\pm x)$、$\cos(\pm x)$の微分は、元の関数の$x$に$\displaystyle x+\frac{\pi}{2}$を代入する。
$\sin(\pm x)$、$\cos(\pm x)$の積分は、元の関数の$x$に$\displaystyle x-\frac{\pi}{2}$を代入する。