ラマヌジャンの公式集：ラマヌジャンの出題した問題

$$\frac32\log2=1+\sum^\infty_{n=1}\frac2{(4n)^3-4n}$$
を示せ。

\begin{align} \tag{a}\prod^\infty_{n=1}\l(1+\frac1{n^3}\r)&=\frac1\pi\cosh\frac{\sqrt3\pi}2\\ \tag{b}\prod^\infty_{n=1}\l(1-\frac1{n^3}\r)&=\frac1{3\pi}\cosh\frac{\sqrt3\pi}2 \end{align}
を示せ。また左辺の表示から$(\mathrm{b})=(\mathrm{a})/3$を示せ。

　未知数$x,y,z,p,q,r$に関する方程式
\begin{align} x+y+z&=a\\ px+qx+rz&=b\\ p^2x+q^2y+r^2z&=c\\ p^3x+q^3y+r^3z&=d\\ p^4x+q^4y+r^4z&=e\\ p^5x+q^5y+r^5z&=f \end{align}
は解けることを示せ。また$(a,b,c,d,e,f)=(2,3,4,6,12,32)$の場合についてこれを解け。

$$\frac{x^6-6}{x^2-y}=\frac{y^6-9}{y^2-x}=5(xy-1)$$
を解け。

\begin{align} \sqrt{1+2\sqrt{1+3\sqrt{1+\cdots}}}\\ \sqrt{6+2\sqrt{7+3\sqrt{8+\cdots}}} \end{align}
の値を求めよ。

　正整数$n$に対してある$\frac13<\T<\frac12$が存在して
$$\frac{e^n}2=\sum^{n-1}_{k=0}\frac{n^k}{k!}+\frac{n^n}{n!}\T$$
が成り立つことを示せ。

　$\a\b=\pi$において
$$\sqrt\a\int^\infty_0\frac{e^{-x^2}}{\cosh\a x}dx =\sqrt\b\int^\infty_0\frac{e^{-x^2}}{\cosh\b x}dx$$
が成り立つことを示せ。

\begin{align} \int^{\frac\pi2}_0\t\cot\t\log\sin\t\ d\t&=-\frac{\pi^2}{48}-\frac\pi4(\log2)^2\\ \int^{\frac1{\sqrt2}}_0\frac{\arcsin x}xdx-\frac12\int^1_0\frac{\arctan x}xdx&=\frac\pi8\log2 \end{align}
を示せ。

　オイラー定数
$$\g=\lim_{n\to\infty}\l(\sum^n_{k=1}\frac1k-\log n\r)$$
は
$$\log2-\sum^\infty_{n=1}n\sum^{3^{n-1}}_{k=1}\frac2{(\frac{3^n-3}2+3k)^3-(\frac{3^n-3}2+3k)}$$
に等しいことを示せ。

\begin{align} \cfrac1{1-\cfrac{e^{-2\pi}}{1+\cfrac{e^{-4\pi}}{1+\cfrac{e^{-6\pi}}{1+\ddots}}}} &=\l(\sqrt{\frac{5+\sqrt5}2}-\frac{\sqrt5+1}2\r)e^{\frac25\pi}\\ \cfrac1{1-\cfrac{e^{-\pi}}{1+\cfrac{e^{-2\pi}}{1-\cfrac{e^{-3\pi}}{1+\ddots}}}} &=\l(\sqrt{\frac{5-\sqrt5}2}-\frac{\sqrt5-1}2\r)e^{\frac15\pi} \end{align}
を示せ。

　奇数$n\geq1$に対し
$$\int^\infty_0\frac{\sin nx}{\cosh x+\cos x}\frac{dx}x=\frac\pi4$$
が成り立つことを示せ。またこのことから
$$\frac\pi8=\sum^\infty_{k=0}\frac{(-1)^k}{2k+1}\l(\cosh\frac{2k+1}{2n}\pi+\cos\frac{2k+1}{2n}\pi\r)^{-1}$$
が成り立つことを示せ。

　$4$の倍数$n\neq0$に対し
$$\sum^\infty_{k=0}(-1)^k\frac{(2k+1)^{n-1}}{\cosh\frac{2k+1}2\pi}=0$$
が成り立つことを示せ。

$$\sin(x+y)=2\sin\frac{x-y}2,\quad\sin(y+z)=2\sin\frac{y-z}2$$
において
$$\l(\frac{\sin x\cos z}2\r)^{\frac14}+\l(\frac{\cos x\sin z}2\r)^{\frac14}=(\sin2y)^{\frac1{12}}$$
が成り立つことを示せ。また実際これが
$$\sin2x=(\sqrt5-2)^3(4+\sqrt{15})^2,\quad\sin2y=\sqrt5-2,\quad\sin2z=(\sqrt5-2)^3(4-\sqrt{15})^2$$
の場合について成り立つことを確認せよ。

$$\int^\infty_0\frac{dx}{\prod^\infty_{n=0}(1+r^nx^2)}=\frac\pi2\frac1{\sum^\infty_{n=0}r^{\frac{n(n+1)}2}}$$
を示せ。

$$\sum^\infty_{n=1}\frac{n}{e^{2\pi n}-1}=\frac1{24}-\frac1{8\pi}$$
を示せ。

　二次形式の積
$$(Ax^2+Bxy+Cy^2)(Ap^2+Bpq+Cq^2)$$
を再び$Au^2+Buv+Cv^2$の形に表せ。またそのことから
$$(2x^2+3xy+5y^2)(2p^2+3pq+5q^2)=2u^2+3uv+5v^2$$
を満たすような$u,v$の一つとして
$$u=\frac52(x+y)(p+q)-2xp,\quad v=2qy-(x+y)(p+q)$$
が成り立つを示せ。

$$(6a^2-4ab+4b^2)^3=(3a^2+5ab-5b^2)^3+(4a^2-4ab+6b^2)^3+(5a^2-5ab-3b^2)^3$$
を示せ。また同様の関係式(おそらく
$$P^3=Q^3+R^3+S^3$$
という恒等式のこと)を満たす別の二次式を見つけよ。

$$\int^\infty_0\frac{\cos tx}{e^{2\pi\sqrt x}-1}dx=\phi(t)$$
とおくと
$$\int^\infty_0\frac{\sin tx}{e^{2\pi\sqrt x}-1}dx=\phi(t)-\frac1{2t}+\phi\l(\frac{\pi^2}t\r)\sqrt{\frac{2\pi^3}{t^3}}$$
が成り立つ。$\phi(t)$を求めよ。特に
\begin{gather} \phi(0)=\frac1{12},\quad\phi\l(\frac\pi2\r)=\frac1{4\pi},\quad\phi(\pi)=\frac{2-\sqrt2}8\\ \phi(2\pi)=\frac1{16},\quad\phi(\infty)=0 \end{gather}
を示せ。

　$2^n-7$は$n=3,4,5,7,15$のとき平方数となる。このような$n$を他にも求めよ。

　$n!+1$は$n=4,5,7$のとき平方数となる。このような$n$を他にも求めよ。

$$\prod^\infty_{n=1}(1+e^{-(2n-1)\pi\sqrt{55}})=\frac{1+\sqrt{3+2\sqrt5}}{\sqrt2}e^{-\frac1{24}\pi\sqrt{55}}$$
を示せ。

$$x^2=y+a,\quad y^2=z+a,\quad z^2=x+a$$
を解け。またそのことから
\begin{align} \sqrt{8-\sqrt{8+\sqrt{8-\cdots}}}&=1+2\sqrt3\sin20^\circ\\ \sqrt{11-2\sqrt{11+2\sqrt{11-\cdots}}}&=1+4\sin10^\circ\\ \sqrt{23-2\sqrt{23+2\sqrt{23-\cdots}}}&=1+4\sqrt3\sin20^\circ\\ \end{align}
を示せ。

\begin{align} \sqrt[3]{\cos\frac{2\pi}7}+\sqrt[3]{\cos\frac{4\pi}7}+\sqrt[3]{\cos\frac{8\pi}7} &=\sqrt[3]{\frac{5-3\sqrt[3]7}2}\\ \sqrt[3]{\cos\frac{2\pi}9}+\sqrt[3]{\cos\frac{4\pi}9}+\sqrt[3]{\cos\frac{8\pi}9} &=\sqrt[3]{\frac{3\sqrt[3]9-6}2} \end{align}
を示せ。

\begin{align} \sqrt{\sqrt[3]5-\sqrt[3]4}&=\farc{\sqrt[3]2+\sqrt[3]{20}-\sqrt[3]{25}}3\\ \sqrt{\sqrt[3]{28}-\sqrt[3]{27}}&=\frac{\sqrt[3]{98}-\sqrt[3]{28}-1}3 \end{align}
を示せ。

$$\frac1x>\sum^\infty_{n=1}\frac{n^{n-2}}{(x+n)^n}\quad(x>0)$$
を示せ。また$x$が十分大きいときの誤差を推定せよ。特に
$$\sum^\infty_{n=1}\frac{n^{n-2}}{(1000+n)^n}\fallingdotseq\frac1{1000}-10^{-440}$$
を示せ。

$$\sum^\infty_{n=0}\frac1{(2n+1)!!}+\cfrac1{1+\cfrac1{1+\cfrac2{1+\cfrac3{1+\cfrac4{1+\ddots}}}}}=\sqrt{\frac{\pi e}2}$$
を示せ。

\begin{align} \sum^\infty_{n=0}\frac{(2n)!!}{(2n+1)(2n+1)!!}\l(\frac13-\frac1{4^{n+1}}\r) &=\frac\pi{12}\log(2+\sqrt3)\\ \sum^\infty_{n=0}(-1)^n\frac{(2n)!!}{(2n+1)(2n+1)!!}&=\frac{\pi^2}8-\frac12(\log(1+\sqrt2))^2 \end{align}
を示せ。

$$\frac\pi2\a=\log\tan\l(\farc\pi4(1+\b)\r)$$
において
$$\prod^\infty_{n=1}\l(\frac{(2n-1)^2-\b^2}{(2n-1)^2+\a^2}\r)^{(-1)^n(2n-1)}=e^{\frac\pi2\a\b}$$
を示せ。

\begin{align} \sum^\infty_{n=0}\frac{x^{n^2}}{\prod^n_{k=1}(1-x^k)} &=\prod^\infty_{n=1}\frac1{(1-x^{5n-4})(1-x^{5n-1})}\\ \sum^\infty_{n=0}\frac{x^{n(n+1)}}{\prod^n_{k=1}(1-x^k)} &=\prod^\infty_{n=1}\frac1{(1-x^{5n-3})(1-x^{5n-2})} \end{align}

$$\lim_{x\to\infty}\frac{(x+a-b)!(8x+2b)!(9x+a+b)!}{(3x+a-c)!(3x+a-b+c)!(12x+3b)!}=\sqrt{\frac23}$$
を示せ。

$$\sum^\infty_{n=0}\frac{(\sqrt5-2)^{2n+1}}{(2n+1)^2}=\frac{\pi^2}{24}-\frac1{12}(\log(2+\sqrt5))^2$$
を示せ。

$$\frac12+\sum^\infty_{n=1}e^{-\pi n^2x}\cos(\pi n^2\sqrt{1-x^2}) =\frac{\sqrt2+\sqrt{1+x}}{\sqrt{1-x}}\sum^\infty_{n=1}e^{-\pi n^2x}\sin(\pi n^2\sqrt{1-x^2})$$
を示せ。またそのことから
\begin{align} \frac12+\sum^\infty_{n=1}e^{-\pi n^2}&=\sqrt{5\sqrt5-10}\l(\frac12+\sum^\infty_{n=1}e^{-5\pi n^2}\r)\\ \sum^\infty_{n=1}e^{-\pi n^2}\l(\pi n^2-\frac14\r)&=\frac18 \end{align}
を示せ。

\begin{align} \sum^\infty_{n=0}\l(\sum^n_{k=0}\frac1{2k+1}\r)\frac{5^{-n}}{2n+1}&=\frac{\pi^2}{4\sqrt5}\\ \sum^\infty_{n=0}\l(\sum^n_{k=0}\frac1{2k+1}\r)\frac{9^{-n}}{2n+1} &=\frac{\pi^2}8-\frac38(\log2)^2\\ \end{align}
を示せ。

　整数の範囲で
$$x^3+y^3+z^3=u^6$$
を解け。またそのことから
\begin{align} 6^3-5^3-3^3&=2^6& 8^3+6^3+1^3&=3^6\\ 12^3-10^3+1^3&=3^6& 46^3-37^3-3^3&=6^6\\ 174^3+133^3-45^3&=14^6& 1188^3-509^3-3^3&=34^6 \end{align}
を示せ。

　翻訳が面倒なので割愛。
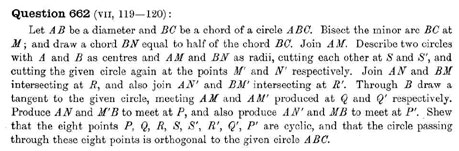Collected Papersより

　正の有理数の範囲で
$$x^y=y^x$$
を解け。例えば
$$(x,y)=(4,2),(27/8,9/4)$$
はこれを満たす。

　整数の範囲で
$$x^3+y^3+z^3=1$$
を解け。またそのことから
\begin{align} 6^3+8^3&=9^3-1\\ 9^3+10^3&=12^3+1\\ 135^3+138^3&=172^3-1\\ 791^3+812^3&=1010^3-1\\ 11161^3+11468^3&=14258^3+1\\ 65601^3+67402^3&=83802^3+1 \end{align}
を示せ。

　$A+\sqrt[3]B$という形の無理数の三乗根の求め方を提示せよ。またそのことから
$$\sqrt[3]{\sqrt[3]2-1}=\sqrt[3]{\frac19}-\sqrt[3]{\frac29}+\sqrt[3]{\frac49}$$
を示せ。

　方程式
\begin{align} x^6-x^3+x^2+2x-1&=0\\ x^6+x^5-x^3-x^2-x+1&=0 \end{align}
の解はそれぞれ根号を用いて表せることを示せ。

$$\sum^n_{k=1}(a+b+2k-1)\frac{(a)_k^2}{(b)_k^2}$$
を求めよ。

$$x^2=y+a,\quad y^2=z+a,\quad z^2=u+a,\quad u^2=x+a$$
を解け。またそのことから
$$x=\sqrt{5+\sqrt{5+\sqrt{5-\sqrt{5+x}}}}$$
のとき
$$x=\frac12(2+\sqrt5+\sqrt{15-6\sqrt5})$$
が成り立つこと、および
$$x=\sqrt{5+\sqrt{5-\sqrt{5-\sqrt{5+x}}}}$$
のとき
$$x=\frac14(\sqrt5-2+\sqrt{13-4\sqrt5}+\sqrt{50+12\sqrt5-2\sqrt{68-20\sqrt5}}\ \ )$$
が成り立つことを示せ。

\begin{align} \bigg[\frac n3\bigg]+\l[\frac{n+2}6\r]+\l[\frac{n+4}6\r] &=\bigg[\frac n2\bigg]+\l[\frac{n+3}6\r]\\ \l[\frac12+\sqrt{n+\frac12}\r]&=\l[\frac12+\sqrt{n+\frac14}\r]\\ \l[\sqrt n+\sqrt{n+1}\r]&=\l[\sqrt{4n+2}\r] \end{align}
を示せ。

\begin{align} \sum^n_{k=1}\arctan\frac1{2n+2k-1}&=\sum^n_{k=1}\arctan\frac1{(2k-1)(1+2(2k-1)^2)}\\ \sum^n_{k=1}\arctan\frac1{(2n+2k-1)\sqrt3}&=\sum^n_{k=1}\arctan\frac1{((2k-1)\sqrt3)^3} \end{align}
を示せ。

$$\phi(x)=\sum^\infty_{n=1}\frac{n^{n-2}x^{n-1}}{(n-1)!}e^{-nx}$$
とおいたとき$0\leq x\leq1$において$\phi(x)=1$が成り立ち、$x>1$においては$\phi(x)\neq1$が成り立つことを示せ。また極限
$$\lim_{\epsilon\to0^+}\frac{\phi(1+\epsilon)-\phi(1)}\epsilon$$
を求めよ。

　正整数$n$に対し
$$\int^\infty_0e^{-nx}(\cot x+\coth x)\sin nx\ dx=\frac\pi2\l(\frac{1+e^{-\pi n}}{1-e^{-\pi n}}\r)^{(-1)^n}$$
を示せ。

$$\phi(x)=\l(\frac{e^x[x]!}{x^{[x]}}\r)^2-2\pi x\quad(x>0)$$
とおいたとき、$\phi(x)$は連続関数を定めること、および$x\to\infty$において$\frac\pi3$から$-\frac\pi6$までを振動することを示せ。また$\phi(x)$を微分せよ。

$$\phi(x)=\frac12\log2\pi x-x+\int^x_1\frac{[t]}tdt$$
とおいたとき
$$\limsup_{x\to\infty}x\phi(x)=\frac1{24},\quad\liminf_{x\to\infty}x\phi(x)=-\frac1{12}$$
を示せ。

　ある$\frac1{100}< E<\frac1{30}$が存在し、$x>0$において
$$\l(\frac ex\r)^x\frac{\G(1+x)}{\sqrt\pi}=\sqrt[6]{8x^3+4x^2+x+E}$$
が成り立つことを示せ。

　翻訳が面倒なので割愛。
Collected Papersより

$$\psi(x)=\frac{x+2}{x^2+x+1}$$
とおいたとき、$x>0$において
$$\sum^\infty_{n=1}\frac1{3^n}\psi(x^{3^{-n}})=\frac1{\log x}+\frac1{1-x}$$
が成り立ち、$x<0$において
$$\sum^\infty_{n=1}\frac1{3^n}\psi(x^{3^{-n}})=\frac1{1-x}$$
が成り立つことを示せ。

$$\log2\sum^\infty_{n=2}\frac1{n\log n\log2n}+\sum^\infty_{n=2}\frac{(-1)^n}{n\log n} =\frac1{\log2}$$
を示せ。

　$\d_n$を約数関数$\d_n=\sum_{d\mid n}1$とすると
$$\sum^\infty_{n=0}\frac{(-1)^n}{2n+1}\d_{2n+1}$$
は収束し
$$\sum^\infty_{n=1}\frac{(-1)^{n-1}}n\d_n$$
は正か負の無限大に発散することを示せ。

　$x=y^n-y^{n-1}$において
$$J_n=\int^1_0\frac{\log y}xdx$$
とおくと
$$J_0=\frac{\pi^2}6,\quad J_\frac12=\frac{\pi^2}{10},\quad J_1=\frac{\pi^2}{12},\quad J_2=\frac{\pi^2}{15}$$
および
$$J_n+J_\frac1n=\frac{\pi^2}6$$
が成り立つことを示せ。

　$\{x\}$を$x$の小数部分(つまり$\{x\}=x-[x]$)とすると
\begin{align} \liminf_{N\to\infty}N\{N\sqrt2\}&=\frac1{2\sqrt2}\\ \liminf_{N\to\infty}N\{N\sqrt3\}&=\frac1{\sqrt3}\\ \liminf_{N\to\infty}N\{N\sqrt5\}&=\frac1{2\sqrt5}\\ \liminf_{N\to\infty}N\{N\sqrt6\}&=\frac1{\sqrt6}\\ \liminf_{N\to\infty}N\{N\sqrt7\}&=\frac3{2\sqrt7} \end{align}
および任意の整数$n,p\;(p>0)$に対し
$$\liminf_{N\to\infty}N(\log N)^{1-p}\{Ne^{\frac 2n}\}=0$$
が成り立つことを示せ。また$p=0$においてはこれが成り立たないことも示せ。

$$\sqrt[3]{3(\sqrt[3]{a^3+b^3}-a)(\sqrt[3]{a^3+b^3}-b)} =\sqrt[3]{(a+b)^2}-\sqrt[3]{a^2-ab+b^2}$$
を示せ。これは
$$\sqrt{2(\sqrt{a^2+b^2}-a)(\sqrt{a^2+b^2}-b)}=a+b-\sqrt{a^2+b^2}$$
の類似である。

\begin{align} \int^\infty_0\cfrac{\sin nx}{x+\cfrac1{x+\cfrac2{x+\cfrac3{x+\ddots}}}}dx &=\cfrac{\sqrt{\pi/2}}{n+\cfrac1{n+\cfrac2{n+\cfrac3{n+\ddots}}}}\\ \int^\infty_0\cfrac{\sin(\pi nx/2)}{x+\cfrac{1^2}{x+\cfrac{2^2}{x+\cfrac{3^2}{x+\ddots}}}}dx &=\cfrac1{n+\cfrac{1^2}{n+\cfrac{2^2}{n+\cfrac{3^2}{n+\ddots}}}}\\ \end{align}

\begin{align} \sqrt{\sqrt[5]{\frac15}+\sqrt[5]{\frac45}} &=\sqrt[5]{1+\sqrt[5]2+\sqrt[5]8}\\ &= \sqrt[5]{\frac{16}{125}}+\sqrt[5]{\frac8{125}}+\sqrt[5]{\frac2{125}}-\sqrt[5]{\frac1{125}}\\ \sqrt[3]{\sqrt[5]{\frac{32}5}-\sqrt[5]{\frac{27}5}} &=\sqrt[5]{\frac1{25}}+\sqrt[5]{\frac3{25}}-\sqrt[5]{\frac9{25}}\\ \sqrt[4]{\frac{3+2\sqrt[4]5}{3-2\sqrt[4]5}} &=\frac{\sqrt[4]5+1}{\sqrt[4]5-1} \end{align}
を示せ。

\begin{align} \sqrt[6]{7\sqrt[3]{20}-19}&=\sqrt[3]{\frac53}-\sqrt[3]{\frac23}\\ \sqrt[8]{4\sqrt[3]{\frac23}-5\sqrt[3]{\frac13}} &=\sqrt[3]{\frac49}-\sqrt[3]{\frac29}+\sqrt[3]{\frac19} \end{align}
を示せ。