JMO2026予選幾何解説

488

　幾何はなんとか全部倒せたので解説します．（図は試験中に書いたものです）

問題3

　とりあえず $\triangle ABP=\triangle AQE=9$ ですね．なので $\triangle APE$ と $\triangle BPC$ の相似とかを面積比と絡めて見ると，
$BQ:QD=\sqrt{18}:\sqrt{3}\ ,\ EP:PC=\sqrt{18}:\sqrt{3}$ すなわち $PC:QD=\sqrt{3}:\sqrt{2}$ であると分かります．再び面積比から $AC=\dfrac{11}2PC\ ,\ AD=4QD$ が分かるので，$\dfrac{AC}{AD}=\dfrac{11}2\sqrt{2}\times \dfrac{1}{4\sqrt3}=\dfrac{11\sqrt6}{24}$ と求まりました．

問題6

　$M$ に関し $B,C$ と対称な点をそれぞれ $B',C'$ とします．このとき $C'BCB'$ は平行四辺形で，$AC'=EC=3$ です．$AB=x$ とおくと，$FD:BC=B'D:B'C=C'A:C'B=3:(x+3)$ で，$FD=3$ なので $BC=x+3$ です．また，$BC$ の中点を $N$ とすれば，$MN=\dfrac{AB+EC}2=\dfrac{x+3}2$ で，これは $BN=CN$ と等しいので $\angle BMC=90^\circ$ が分かります．よって $BC=\sqrt{BM^2+CM^2}=\sqrt{41}=x+3$ であり，$AB=x=\sqrt{41}-3$ と求まりました．

問題9

　$\angle BRC=\angle RDQ=180^\circ-\dfrac12\angle BAC$ より，$AB=AC=AR=6\sqrt7$ と分かります．（すなわち $A$ は $\triangle BRC$ の外心で，ここで図を再構築すると良いです．）
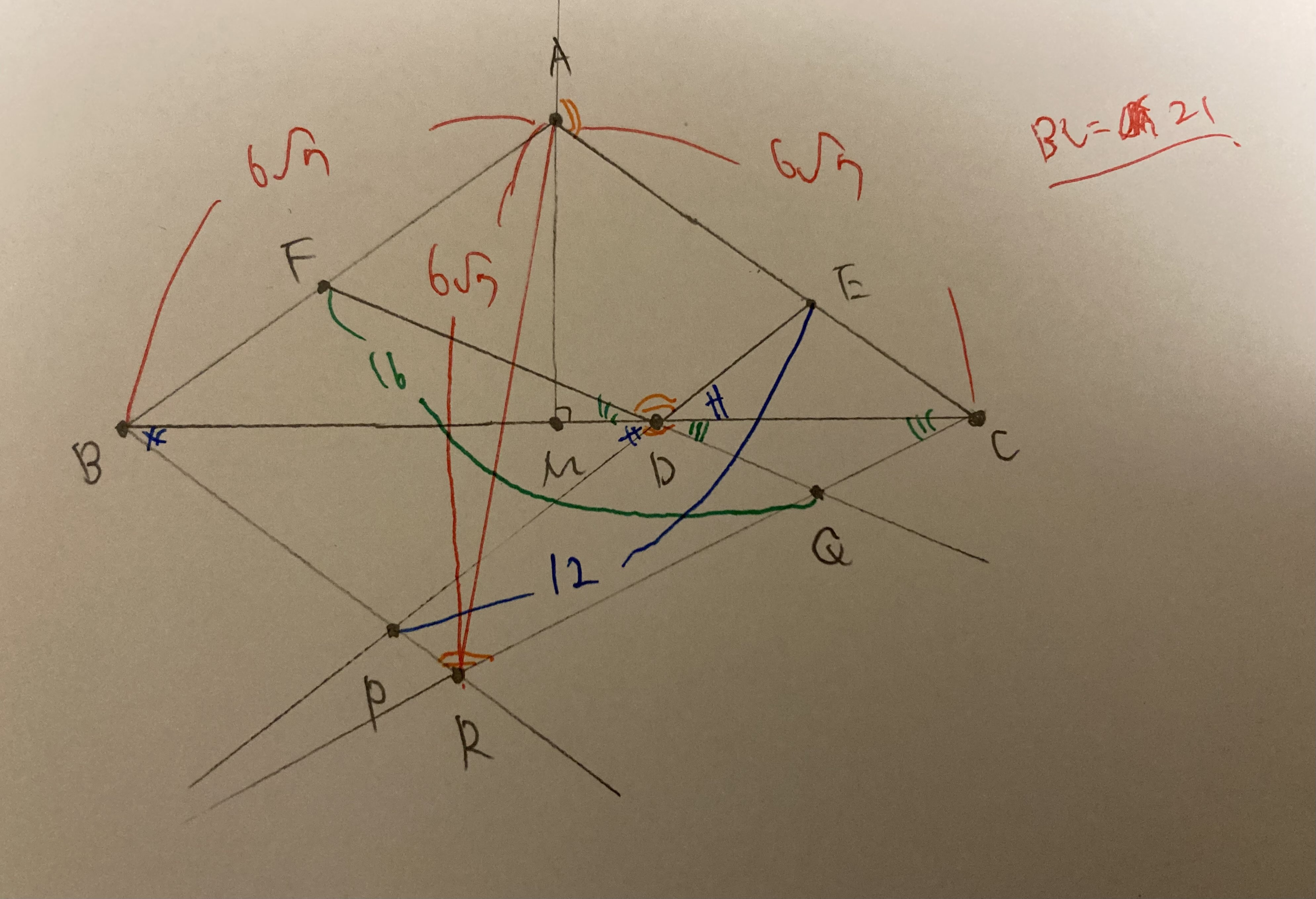色ペンを使うと，見やすいかも
　$PD=PB=PF$ が成り立っていそうなので示します．これは適当に開けば示せて，$\angle BFD=180^\circ-\angle ABD-\angle FDB=180^\circ-\angle ACR$ および $\angle DPR=2\angle RBC=\angle RAC=180^\circ-2\angle ACR$ から分かります．
　これからいろいろなことが分かります．まず $\angle PFD=\angle PDF=\angle QDE=\angle QED$ より $F,P,Q,E$ は共円です．さらに，$\angle DEQ=\angle EDQ=180^\circ-\angle PDQ=180^\circ-\angle PRQ$ から $R$ が円 $FPQE$ 上にあることも従います（使いませんが）．
※追記：$A$ もこの円周上にあることが同じような角度計算で示せます．
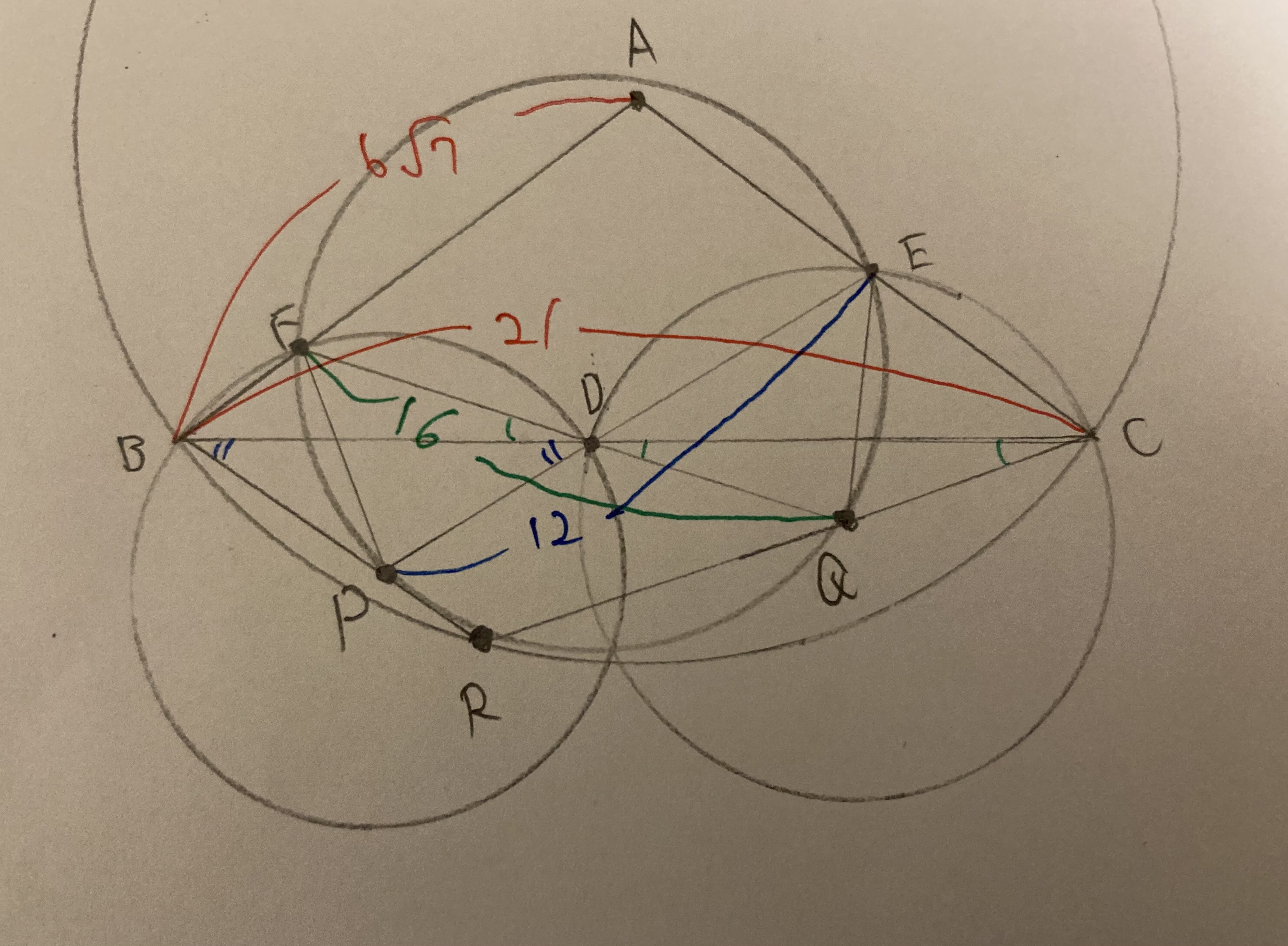色ペンを使うと，見やすいかも
　$\sin \angle BAC$ が求まることから大体すべてが分かる気がするので計算しましょう．普通にやれば分かるので省略しますが $FD:DP=ED:DQ=3:2$ です．$EP=12\ ,\ FQ=16$ から連立して解くと $DP=\dfrac{48}5\ ,\ DQ=\dfrac85$ が分かります．$Q$ から $PD$ に下ろした垂線の長さは $\dfrac25\sqrt{7}$ であることから，$\triangle DPQ=\dfrac{48\sqrt7}{25}$ と求まりました．
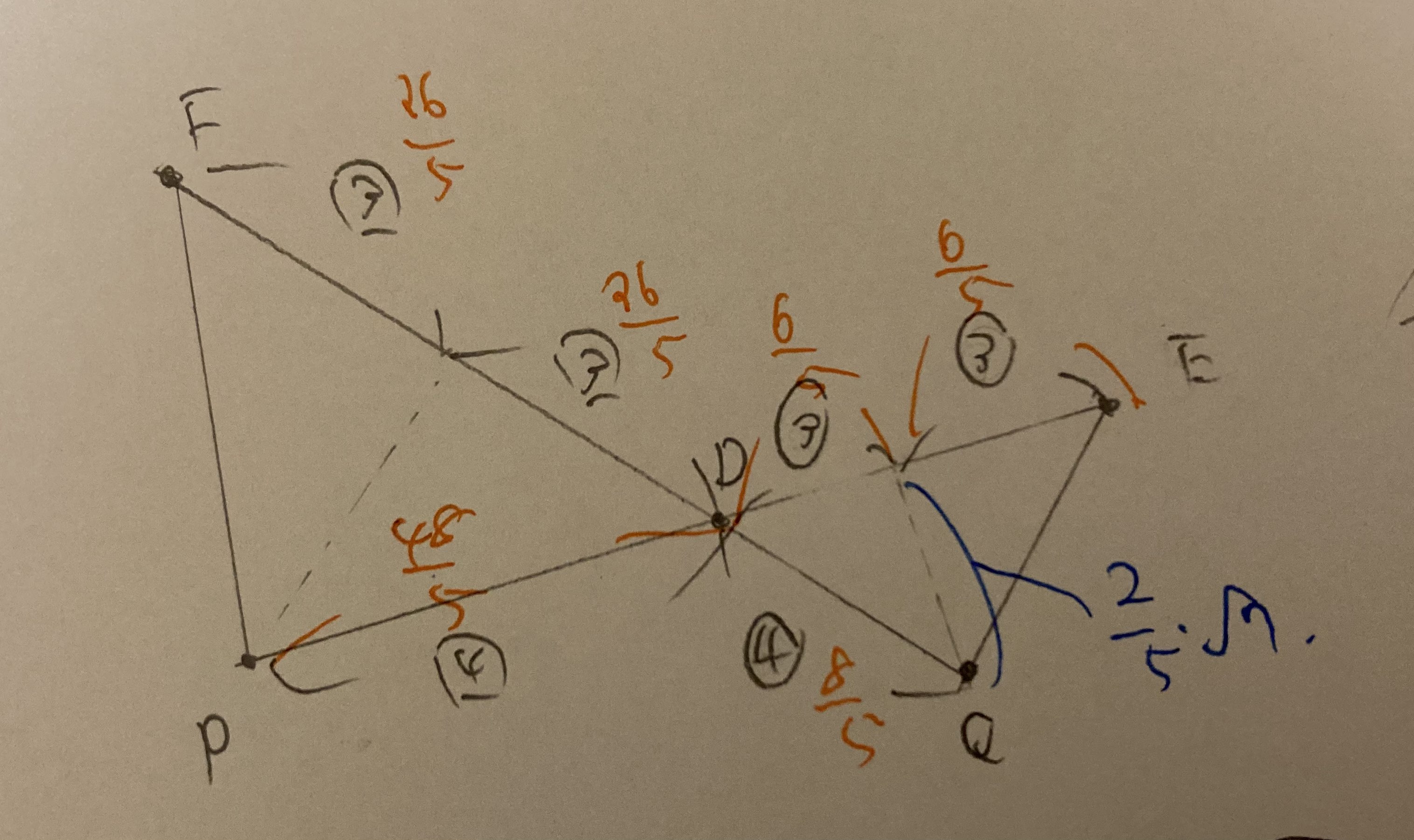色ペンを使うと，見やすいかも