軌跡領域•同値変形まとめ

1.はじめに

知っておくべきこと

代入の原理

$\begin{eqnarray} \left\{ \begin{array}{l} y=f(x) \\ g(x,y)=0 \end{array} \right. \douchi \left\{ \begin{array}{l} y=f(x) \\ g(x,f(x))=0 \end{array} \right. \end{eqnarray} $

存在条件の代入原理

$\dis\begin{eqnarray} {}^{\ex}x\left\{ \begin{array}{l} x=a \\ f(x) \end{array} \right. \douchi f(a) \end{eqnarray}$

式で表すと上みたいな感じざっくり言えば代入の原理は式を代入したら代入した式を残して変形すれば同値性は保たれるということ、存在条件の代入原理は存在するものの条件が具体的に分かれば存在条件を消せるということ！
$$\dis\begin{eqnarray} {}^{\ex}t\left\{ \begin{array}{l} x=t+1 \\ y=-t^2\\ t\in \R \end{array} \right. \douchi {}^{\ex}t\left\{ \begin{array}{l} t=x-1 \\ y=-t^2 \\ t\in \R \end{array} \right. \douchi {}^{\ex}t\left\{ \begin{array}{l} t=x-1 \\ y=-(x-1)^2 \\ t\in \R \end{array} \right. \douchi \left\{ \begin{array}{l} y=-(x-1)^2 \\ {}^{\ex}t\{t=x-1_{\and}t\in\R\} \end{array} \right. \douchi \left\{ \begin{array}{l} y=-(x-1)^2 \\ x\in \R \end{array} \right. \end{eqnarray} $$
と言ったような感じ
途中
$\dis {}^{\ex}t\{t\in\R_{\and}t=x-1\}\douchi x-1\in\R\douchi x\in\R$
という変形を省略しました！
同値変形で大切なことは$\textcolor{red}{\text{変形前と変形後を行き来できること！}}$
ですので戻れない変形はしないように気をつけましょう！！

例題

例1 $2$乗の扱いには気をつけて！

$t$が実数値をとって動く時点$(x,y)=(t^2+1,t^4)$の軌跡を$x,y$の式として表せ。

解答

$\dis \begin{eqnarray} {}^{\ex}t\left\{ \begin{array}{l} x=t^2+1 \\ y=t^4 \\ t\in\R \end{array} \right. \douchi {}^{\ex}t\left\{ \begin{array}{l} t^2=x-1 \\ y=t^4 \\ t\in\R \end{array} \right. \douchi \left\{ \begin{array}{l} {}^{\ex}t\{t^2=x-1_{\and}t\in\R\} \\ y=(x-1)^2 \end{array} \right. \douchi \left\{ \begin{array}{l} x-1\geqq 0\\ y=(x-1)^2 \end{array} \right. \end{eqnarray}$

よって求めるべき軌跡の式は

$\dis\begin{eqnarray} \left\{ \begin{array}{l} y=(x-1)^2 \\ x\geqq 1 \end{array} \right. \end{eqnarray}$

注意すべきポイント

$\dis {}^{\ex}t\{t\in\R_{\and}t^2=f(x)\}\douchi f(x)\geqq 0$
という$2$乗に関する変形は意外と忘れがちですが大切なので気をつけましょう！

例2 みんな嫌いなやつ

実数$s,t$が$0\leqq s,t \leqq 1$の範囲を自由に動く時$(x,y)=(st,s+t)$の動く範囲を$x,y$の式で表せ。

解答

$ \dis\begin{eqnarray} {}^{\ex}s,t\left\{ \begin{array}{l} x=st \\ y=s+t \\ 0\leqq s,t \leqq 1 \\ s,t\in\R \end{array} \right. \douchi u\text{についての二次方程式}u^2-xu+y=0\text{が重解を含めて}2\text{つの実数解を持つ} \end{eqnarray} $

二次方程式の解の配置

$a,b$を実数として$x$についての二次方程式$f(x)=x^2-ax+b=0$が$p\leqq x\leqq q$の範囲に2実解（重解を含む）を持つ条件は
$\dis\begin{eqnarray} \left\{ \begin{array}{l} f(p)\geqq0 \\ f(q)\geqq0\\ p\leqq \frac{a}{2} \leqq q \\ D=a^2-4b\geqq0 \end{array} \right. \end{eqnarray}$
$1,2$番目の式は境界条件
$3$番目の式は軸の位置の条件
$4$番目の式は解を持つ条件（判別式）
これは一瞬で当たり前にすべきなので忘れたらその都度図を書いて導出しましょう！
また解の範囲にイコールが入っていなかったり異なる２解を持つなど条件が変わることがあるので気をつけましょう！とにかく図を書く！！

$\dis\douchi \begin{eqnarray} \left\{ \begin{array}{l} f(0)\geqq 0\\ f(1)\geqq0\\ 0\leqq \frac{x}{2} \leqq 1 \\ D=x^2-4y\geqq 0 \end{array} \right. \douchi \left\{ \begin{array}{l} y\geqq0\\ 1-x+y\geqq0\\ 0\leqq x \leqq 2 \\ x^2-4y\geqq 0 \end{array} \right. \end{eqnarray} $
これが答え！一応図示するとこんな感じ
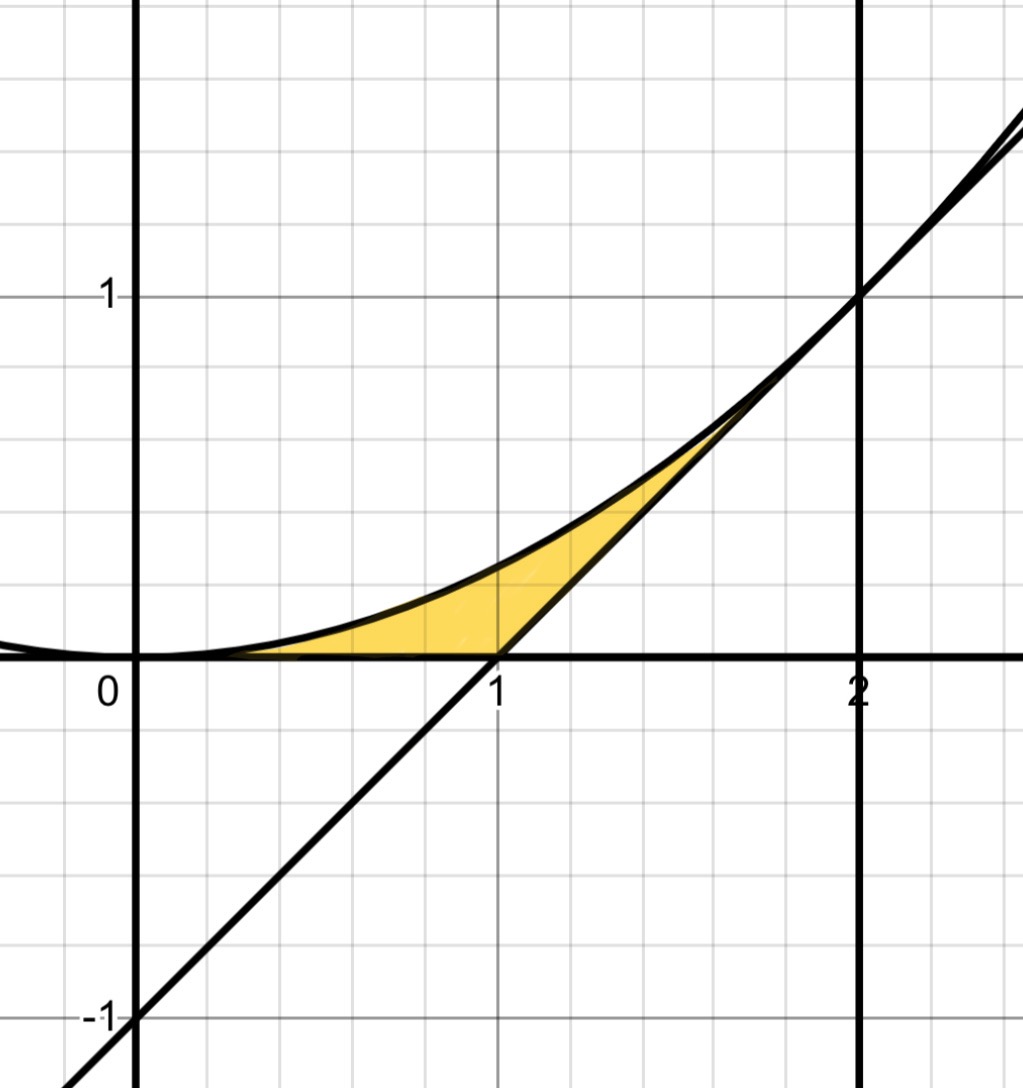黄色部分ただし境界線を全て含む
考え方としては「さかのぼって」で例えば
「$0\leqq s,t \leqq 1$かつ$s+t=1,st=-1$なる実数$s,t$は存在するか？」
なら
「このような$s,t$は$u$の二次方程式$u^2-u-1=0$の2実解だから
$\dis s,t=\frac{1\pm\sqrt{5}}{2}$
これは$0\leqq s,t \leqq 1$を満たさないから不適切！」
のようにもし$x,y$が具体値だったらどう解くかを考えその後具体値のところを文字に変えるとやりやすい！$\textcolor{red}{\text{わからなくなったら具体値で試そう！}}$
~~場合分けが必要だったり図示があんまり楽しくないから僕は嫌い😠~~

例3 加減法の原理

$\dis\begin{eqnarray} \left\{ \begin{array}{l} 2x+3y=8\\ x-y=-1 \end{array} \right. \end{eqnarray}$
を満たすような$x,y$を求めよ。
&

解答

突然簡単になったと思うけど大事だから簡単な例で体感してね

加減法の原理

$\begin{eqnarray} \left\{ \begin{array}{l} f(x,y)=0 \\ g(x,y)=0 \end{array} \right. \douchi \left\{ \begin{array}{l} af(x,y)+bg(x,y)=0 \\ cf(x,y)+dg(x,y)=0 \\ ad-bc \neq 0 \end{array} \right. \end{eqnarray}$

なぜ$ad-bc\neq 0$が必要か（タップで表示）

$c=ka,d=kb$のように$c,d$が$a,b$の定数倍となってしまうと$cf(x,y)+dg(x,y)=k(af(x,y)+bg(x,y))=0\douchi af(x,y)+bg(x,y)=0$となり実質的に式が1つになるので元に戻れなくなり、同値変形ではなくなります。また$a=c=0$なら$f(x,y)$に関する式がなくなってしまい元に戻れないので同値変形ではなくなります。（$b=d=0$の場合も同様に$g(x,y)$に関する式がなくなってしまいダメです。）
故に$a:b\neq c:d_{\and}a,c\text{または}b,d\text{が同時に0にならない}\douchi ad-bc\neq 0$なので$ad-bc \neq 0$が条件として必要になります！

加減法の原理を利用すれば

$$ \dis\begin{eqnarray} \left\{ \begin{array}{l} 2x+3y=8 \\ x-y=-1 \end{array} \right. \douchi \left\{ \begin{array}{l} 2x+3y-8=0\cdots① \\ x-y+1=0\cdots② \end{array} \right. \douchi \left\{ \begin{array}{l} ①+②×3=0 \\ ①-②×2=0 \end{array} \right. \douchi \left\{ \begin{array}{l} 5x-5=0 \\ 5y-10=0 \end{array} \right. \douchi \left\{ \begin{array}{l} x=5 \\ y=2 \end{array} \right. \end{eqnarray} $$
既に気づいているかもしれませんがこれは連立方程式を厳密に解いてるだけです！
正確な同値変形で解こうとするとだいぶ面倒ですが、このような同値変形が大切になることもありますよ！！
【別解】代入法で解く

$\dis\begin{eqnarray} \left\{ \begin{array}{l} 2x+3y=8\\ x-y=-1 \end{array} \right. \douchi \left\{ \begin{array}{l} 2x+3y=8\\ y=x+1 \end{array} \right. \douchi \left\{ \begin{array}{l} 2x+3(x+1)=8\\ y=x+1 \end{array} \right. \douchi \left\{ \begin{array}{l} x=1\\ y=x+1 \end{array} \right. \douchi \left\{ \begin{array}{l} x=1\\ y=2 \end{array} \right. \end{eqnarray}$
のよう！代入した式を残すのを忘れずに！

例4 基本公式の利用

$xy$平面上で媒介変数$t$を用いて
$\begin{eqnarray} \left\{ \begin{array}{l} x=\sin t+\cos t \\ y=\sin t-\cos t \\ 0\leqq t \leqq \pi \end{array} \right. \end{eqnarray}$
で表される曲線$C$を$t$を含まない$x,y$のみの式で表せ。

解答

三角関数を含む媒介変数表示された曲線から媒介変数を消去する時は大体三角関数の基本公式を使うことで解決できる！

三角関数の基本公式

$①\sin^2 t+\cos^2 t =1$
$②\dis\frac{1}{\cos^2 t}-\tan^2 t=1$
ほとんどの場合①で解決できるけど稀に②を使うとうまくいくやつもあるから覚えておくとよい！

$\begin{eqnarray} \left\{ \begin{array}{l} x=\sin t+\cos t \\ y=\sin t-\cos t \\ 0\leqq t \leqq \pi \end{array} \right. \douchi \left\{ \begin{array}{l} x+y=2\sin t \\ x-y=2\cos t \\ 0\leqq t \leqq \pi \end{array} \right. \douchi \left\{ \begin{array}{l} (\frac{x+y}{2})^2+(\frac{x-y}{2})^2=1 \\ 0 \leqq \frac{x+y}{2} \leqq 1 \\ -1\leqq \frac{x-y}{2} \leqq 1 \end{array} \right. \douchi \left\{ \begin{array}{l} x^2+y^2=2 \\ 0 \leqq x+y \leqq 2 \\ -2\leqq x-y\leqq 2 \end{array} \right. \end{eqnarray}$
これを図示して式を整理すれば求めるべき答えは
$$ \begin{eqnarray} \left\{ \begin{array}{l} x^2+y^2=2 \\ -x\leqq y \end{array} \right. \end{eqnarray} $$
となります！

注意すること！

$t$の値域を$\mathbb{D}_t$,$\mathbb{D}_t$における$\sin t,\cos t$の値域をそれぞれ$\mathbb{D}_s,\mathbb{D}_c$とすれば

$\begin{eqnarray} \left\{ \begin{array}{l} f(x,y)=\sin t \\ g(x,y)=\cos t\\ t\in\mathbb{D} \end{array} \right. \douchi \left\{ \begin{array}{l} (f(x,y))^2+(g(x,y))^2=1 \\ f(x,y)\in\mathbb{D}_s\\ g(x,y)\in\mathbb{D}_c \end{array} \right. \end{eqnarray}$
$\sin t,\cos t$は値域をもつことに注意しましょう！

例5 重心の存在範囲は？？

$x,y$平面上の$(0,0)$を原点$O$とする。
また放物線$y=x^2$上の2点を$P(p,p^2),Q(q,q^2)$とおく。
この時$\triangle OPQ$の重心$G$の軌跡を$x,y$の式で表せ。

解答

この問題はちょいとむずいです
$OPQ$が三角形とならければいけないので$p\neq q,p\neq 0,q\neq 0\cdots①$に注意します！
$\triangle OPQ$の重心$G$の座標は$O,P,Q$の座標を足し合わせて3で割ったものなので$G$の座標を$(x_G,y_G)$とおけば

$\dis(x_G,y_G)=(\frac{1}{3}(p+q),\frac{1}{3}(p^2+q^2)) \douchi \begin{eqnarray} \left\{ \begin{array}{l} 3x_G=p+q \\ 3y_G=pq \end{array} \right. \end{eqnarray} $

となります！
ここでさかのぼっての考え方を思い出して例えば

「$p+q=3,p^2+q^2=5$となるような$\textcolor{red}{\text{実数}}\;p,q$は存在するか？」

と考えれば

「$p+q=3,pq=2$となるような$p,q$は$t^2-3t+2=0$の2解で判別式は$D=(-3)^2-4×2=1\geqq 0$だから共に実数となる！」

と考えられるので具体値を文字にすれば

「$p+q=3x_G,p^2+q^2=3y_G$となるような$\text{実数}\;p,q$は存在するか？」

と考えて

「$\dis p+q=3x_G,pq=\frac{1}{2}(9x_G^2-3y_G)$となるような$p,q$は$\dis t^2-3x_Gt+\frac{1}{2}(9x_G^2-3y_G)=0$の2解で判別式は$D=9x_G^2-4×\frac{1}{2}(9x_G^2-3y_G)$だからこれが$\geqq 0$となれば共に実数となる！」

となります！ここで①の条件をふまえれば
判別式が0となると重解を持ってしまうので
判別式$D\gt 0$が必要だとわかります！
また$p,q$のどちらかが0になってしまうと$pq$も0になってしまうので$\dis pq=\frac{1}{2}(9x_G^2-3y_G)\neq 0$
以上より

$$ \begin{eqnarray} \left\{ \begin{array}{l} -9x_G^2+6y_G\gt 0 \\ \frac{1}{2}(9x_G^2-3y_G)\neq 0 \end{array} \right. \douchi \left\{ \begin{array}{l} 2y_G\gt 3x_G^2 \\ 3x_G^2\neq y_G \end{array} \right. \end{eqnarray} $$
よって求めるべき軌跡は
$$ \begin{eqnarray} \left\{ \begin{array}{l} 2y\gt 3x^2 \\ 3x^2\neq y \end{array} \right. \end{eqnarray} $$
一応図はこんな感じです
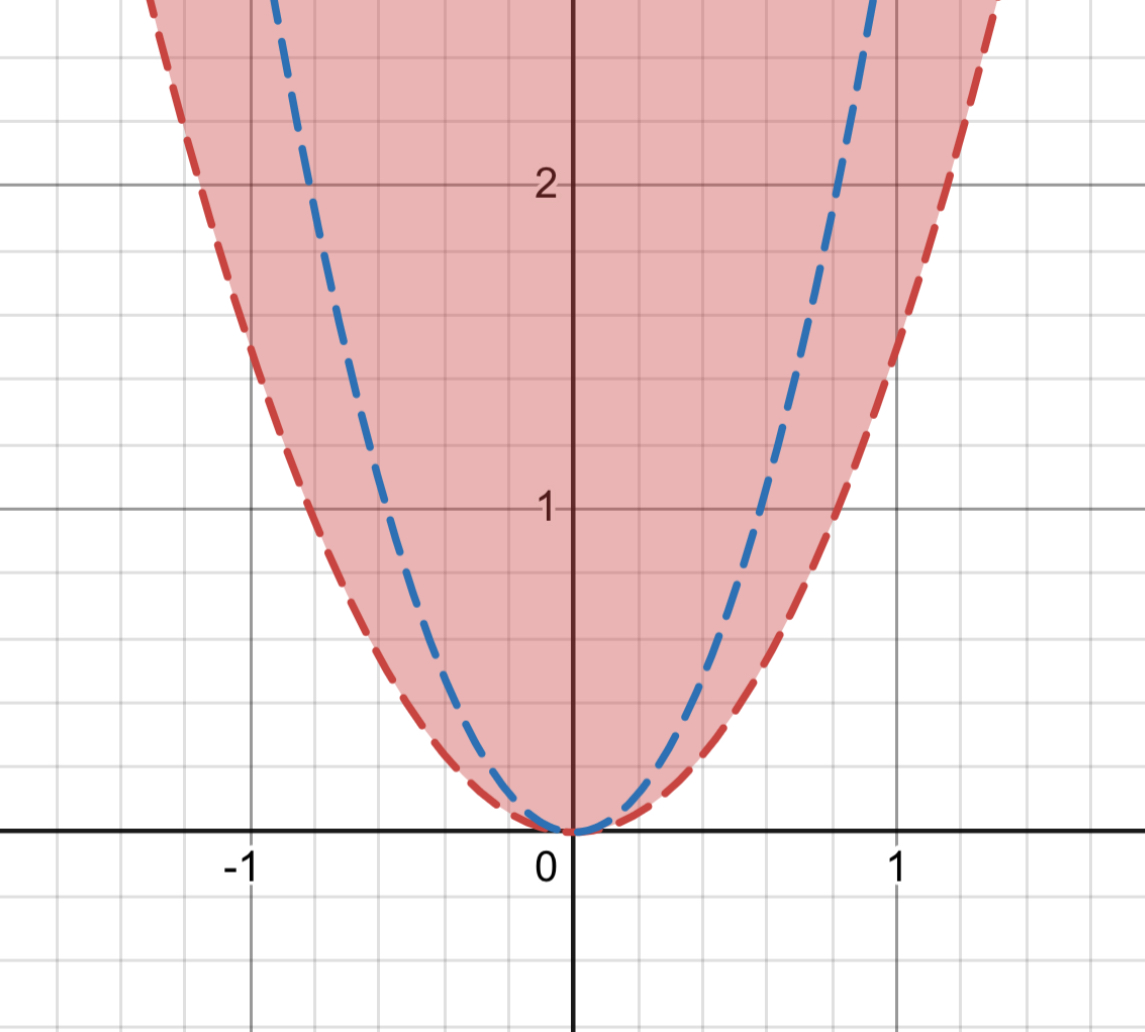赤い範囲ただし点線は全て含まない