除夜の鐘コンテスト　自作問題の解説

122

ぽもどーろさん（X：@1468_math）主催の除夜の鐘コンテストでWriterをしていたので解説を書きます．

組み合わせコンテストP5

平面上の$3$つ以上の点からなる集合$S$があり，どの$S$内の$3$点も同一直線上にはないとする．ある$S$の三角形分割$T=(\triangle _1, \triangle _2, \ldots , \triangle _n)$が存在し，適切に$\triangle_i$を選んで始点とすることで，辺を共有する三角形への移動を繰り返すことで全ての$T$の元をちょうど一回ずつ通ることが可能であることを示せ．ただし，$T$は以下を満たすような（内部の詰まった）三角形の集合である．

任意の$i \neq j$に対し，$\triangle _i$と$\triangle _j$は境界以外で共有点を持たない．
$\triangle _1, \triangle _2, \ldots , \triangle _n$の頂点全体からなる集合は$S$に一致する．
$\triangle _1, \triangle _2, \ldots , \triangle _n$の和集合を$P$としたとき，任意の$X, Y, Z \in S$に対し，三角形$XYZ$は$P$に含まれる．

略解

$S$の点を外側からぐるぐる巻いて折れ線をとり（$J,H,C,D,\ldots$），それに沿って三角形を取る（$\triangle JIE, \triangle JEH, \triangle HEA, \ldots$）ことで条件を満たす．
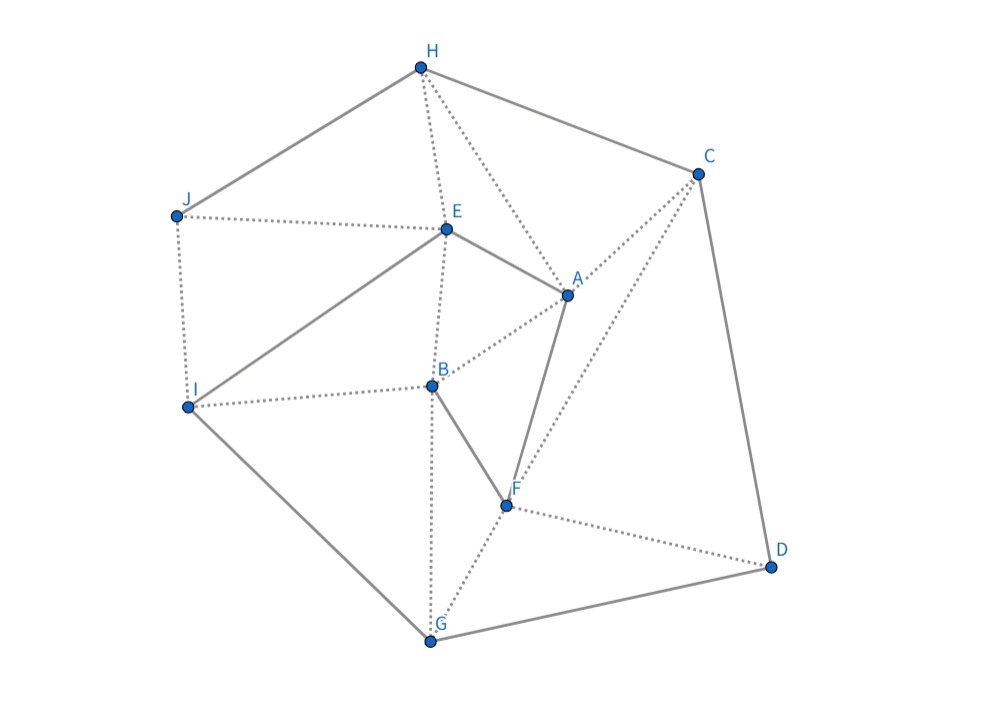Geogebraで作成

整数コンテストP5

正の整数からなる数列$\{a_n\}, \{b_n\}$は任意の正の整数$n$に対して以下を満たす．
$$a_{n+1}^2=a_n^2b_n+1$$
このとき，任意の実数$M$に対し，ある正の整数$n$が存在して$b_n>M$が成り立つことを示せ．

解答

　数列$\{b_n\}$が有界であると仮定し，矛盾を導く．$b_n$が取り得る値全体からなる集合を$B$とする．$\{b_n\}$の連続する$|B|+1$項の中に値が等しい$2$項があり，このような組は無数に存在する．よって鳩の巣原理から，ある$d,d_1,\ldots ,d_m \in B$が存在し，無数に多くの$n$に対して
\begin{align*} a_{n+1}^2-da_n^2 &= 1 \\ a_{n+2}^2-d_1a_{n+1}^2 &= 1 \\ &\vdots \\ a_{n+m+1}^2-d_ma_{n+m}^2 &= 1\\ a_{n+m+2}^2-da_{n+m+1}^2 &= 1\\ \end{align*}
が成り立つ．ここで，
\begin{align*} \lim_{n \to \infty} \frac{a_{n+m+1}}{a_n} = \sqrt{dd_1d_2\cdots d_m} \quad \cdots (1) \end{align*}
となる．一方，Pell方程式に関する well-known fact から，正の整数の定数$\alpha, \beta$が存在し，正の整数$k,l$を用いて
\begin{align*} a_n &= \frac{1}{2 \sqrt{d}} \left((\alpha+\beta \sqrt{d})^k - (\alpha-\beta \sqrt{d})^k \right)\\ a_{n+m+1} &= \frac{1}{2 \sqrt{d}} \left((\alpha+\beta \sqrt{d})^l - (\alpha-\beta \sqrt{d})^l \right)\\ \end{align*}
と表せる．(1)より$l-k$は十分先で一定であり，この値を$C$とすれば，$n \to \infty$を考えることで
$$\sqrt{dd_1d_2\cdots d_m} = (\alpha + \beta \sqrt{d})^C$$
となって矛盾する．よって題意は示された．