PoC001(F), F-Plus-Minus Array　解説

　 PoC(Project orangekid Contest) は、 Project Euler のように、競技プログラミングで数学の問題を解くコンテストです。

PoC001(F), F-Plus-Minus Array 解説

　次のような問題です。

正しくは$2\leq r\leq10^6+1$です。本当に申し訳ございません。
　まず考えられるのはDP(動的計画法)ですが、この範囲だと明らかに間に合いませんね。実際に小さい方から実験して、法則を探してみましょう。
　横軸を$i$、縦軸を$a_i$として$xy$平面上にありうる点をプロットすると、図1のようになります。
$r=13$の場合
　この図から、$r$が偶数の時、条件を満たす数列がないことが容易にわかります。そこで、長さが$r$($r$は3以上の奇数)のときの、条件を満たす数列の数を$P_n$と置きましょう。図1を回転させると、次の図2を得ます。
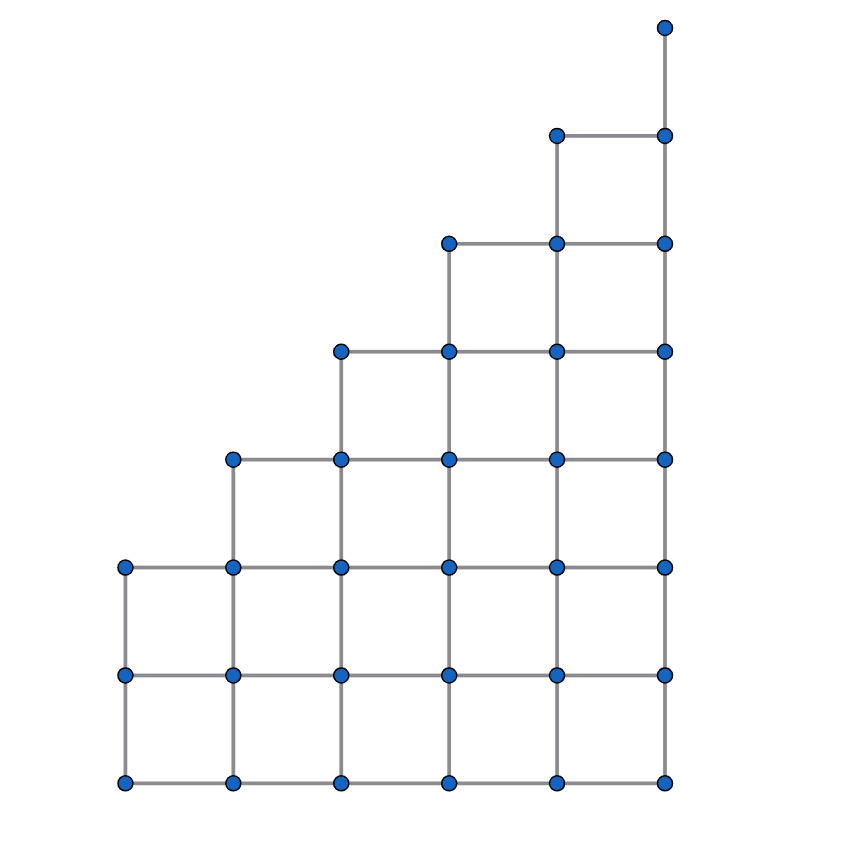回転後
　$P_n$はこの図の左下端から右上端まで、最短距離で移動する方法の数に等しいですね。
　ここで、次の図3について考えてみましょう。

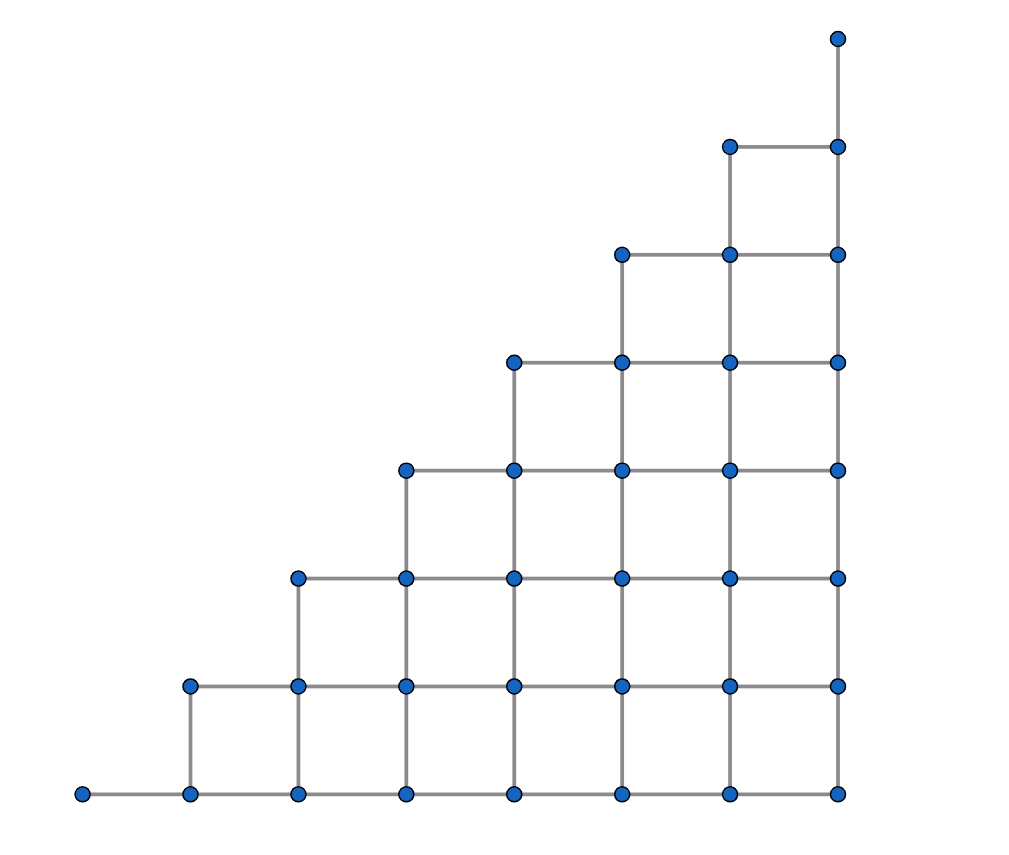
　この図形の左下端から右上端まで、最短距離で移動する方法の数は、カタラン数を用いて求めることが出来ます。

　証明はネットに転がっているので各自で調べてください。
　
　したがって、図3の場合は$C_7$通りあることになります。
　また、図3の左下端から右上端まで行く方法は、次の2パターンに分けられます。

1. 最初の分かれ道で上に進む
2. 最初の分かれ道で右に進む

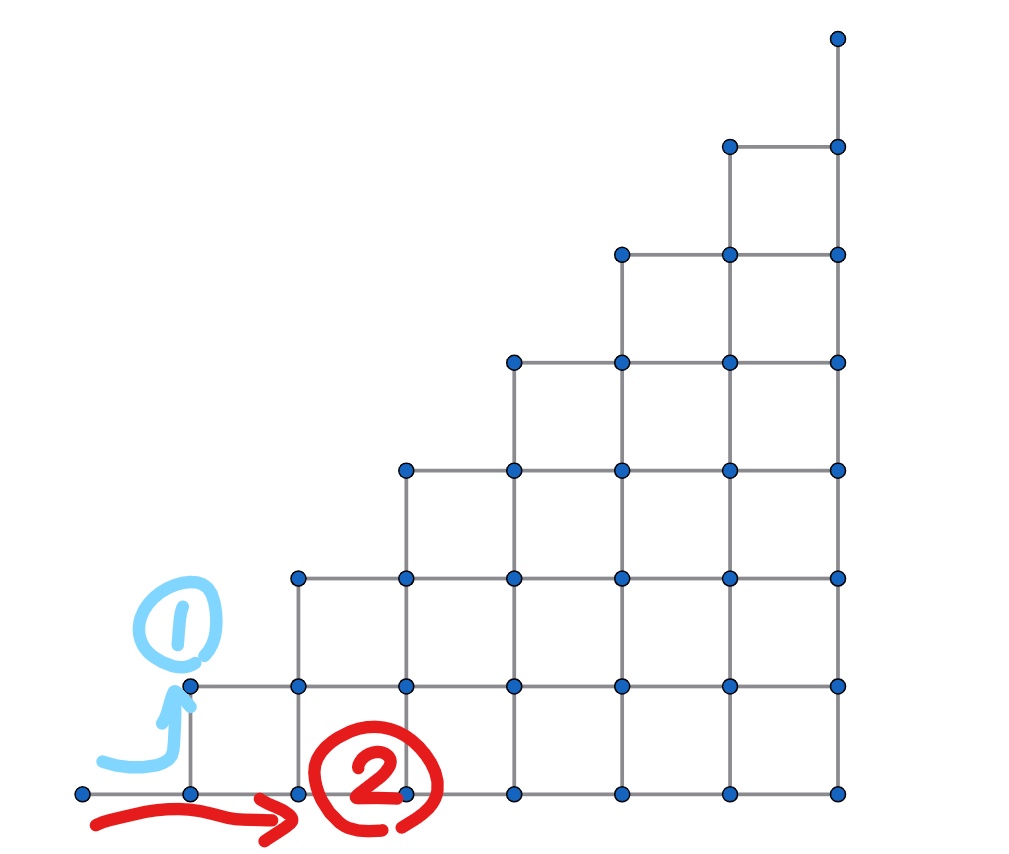2パターン
　図4より、パターン1のときは$C_6$通り、パターン2のときは$P_{13}$通りあることが分かりますね。したがって、
$P_{13}=C_7-C_6$
と表すことが出来ます。
　$r$の値が違う場合も同様に考えていくと、求める値($=P_n$の総和)は、
$$ \sum_{i=1}^{5\times 10^5}(C_{i+1}-C_i)=C_{5\times10^5+1}-C_1 $$
となるので、後は計算すればよいです。modで割り算は扱いにくいですが、$998244353$は素数なので、$a^{998244353-2}$が$a$の$\mod 998244353$での逆元(逆数に対応する)になります。以上をプログラムすると、答は$122657580$と求まります。

サンプルコード(Python)

      mod = 998244353
N = 500001
a, b = 1, 1
for i in range(1, N + 1):
    a = a * (i + N) % mod
    b = b * i % mod
b = pow(b * (N + 1), mod - 2, mod)
ans = a * b - 1
print(ans % mod)