高校数学議論

文献あり

ある加群上の分解とそのwell-defined

超幾何数列,数列,約分

329

こんにちは。Mark6という者です。
この記事の主題は、ある写像のwell-defined性を、あの整数論の大定理を援用して示すことです。

どうやら子葉さんの記事を読む限り、超幾何数列の話に関係がありそうなんですが、怖すぎて先行研究を調べないまま公開します。ごめんなさい。

経緯とモチベ

最近下のような式を大量にいじくり回す機会がありました。

恒等式

整数$n \geq 2$について下の式が成り立つ。
$$\sum_{k=1}^{n}\frac{(-1)^k(3k-2)(2k-2)!(2n+k-3)!}{k!(k-1)!(n+2k-2)!(n-k)!}=0$$

証明は読者に任せます(言ってみたかった)。
この記事では別のことについて書きたいと思います。

上の式のシグマの中の式から$(-1)^k$を取り払い、$(3k-2)$を$(3k-2)!/(3k-3)!$と書き直すと
$$\frac{(3k-2)!(2k-2)!(2n+k-3)!}{k!(k-1)!(3k-3)!(n+2k-2)!(n-k)!}$$
となります。分母分子が複数の$(an+bk+c)!$の積で書けました。

上のような式の簡略化として、下の式について考えてみます。

$$6(n+1)(2n+1)!(3n+2)!$$

この式の表示には、ある種の冗長性があります。

\begin{align} & 6(n+1)(2n+1)!(3n+2)! \\ &= 3(2n+2)!(3n+2)! \\ &= 2(2n+1)!(3n+3)! \end{align}

表示方法が複数あること自体は受け入れるとしても、その構造についてもう少し理解したくなりました。
この記事ではこの問いを、環上の加群のあたりの言葉を使って定式化したのち、うまい写像を構成してこの「表示揺れ」のひとつの支点の姿を明らかにします。

予防線

最低限数学的な間違いは無いよう気をつけていますが、この記事の内容は、独りよがりなモチベから始まり、ただ楽しい方向に進んだだけの、数学という学問からすればおそらく邪道も甚だしいであろう議論です。
あとこの記事は、環上の加群についてpdf１枚とWikipediaしか調べていないという、基礎カスの記事です。

定式化の概観

① まず考える対象とする式、つまり
$$f(n,k)=\prod_{i=1}^N [(a_in+b_ik+c_i)!]^{\pm e_i}$$
のように書ける$f(n,k)$のことを「ユニット」と呼ぶことにします。
このユニットは、通常の意味での積を演算として、群を成します。

② 「ユニットの表示方法」を考える上でユニットそのものを使うことはできません。例えば
$$\frac{(2n)!k!}{(2n-1)!(k-1)!}=\frac{n!(2k)!}{(n-1)!(2k-1)!}$$
は、$n,k$の関数としては全く同じなので、ユニットとして扱っている限りは区別することができません。

ユニットの表示方法を考える上では、これらを区別し、それぞれの表示を構成する$(2n)!$などを分離して扱うことができるような枠組みが必要です。

③ この記事ではその枠組みとして「骨格」と呼ぶ対象を導入します。
ユニット
$$\prod_{i=1}^N [(a_in+b_ik+c_i)!]^{e_i}$$
に対応して
$$\sum_{i=1}^N e_i(a_i,b_i,c_i)$$
という形式和のことを骨格と呼びます。骨格には自由加群としての構造が入り、これはある準同型写像を通してユニットの積と対応します。

④ ユニットや骨格に同値関係「合同」を導入します。この同値類が直感的な「表記揺れ」の範囲になっています。
そして「同値類それぞれに代表元を定めたい」として問いを定式化します。
つまり、「ユニット$f,g$が合同なら$\Phi(f)=\Phi(g)$」となるような写像$\Phi$を探します。
表記揺れ全体をひとつの元にまで潰し込むこの写像$\Phi$が、この記事の目標です。

問いの定式化

初心者なので下の定義は非常に読みにくいです。許してください。良い書き方を教えてください。

良い組

下の２条件を満たす整数３つの順序組$(a,b,c)$を「良い組」と呼ぶ。

$a \neq 0$または$b \neq 0$
$n\geq k\geq 1$を満たす任意の整数$n,k$に対して$an+bk+c\geq 0$

良い組の集合を$Y$とする。

Yoikumiなので$Y$です(カス)。

良い組

$(1,2,3)$や$(2,0,-1)$は良い組です。
$(3,-2,-2)$は、$3n-2k-2$に$(n,k)=(1,1)$を代入すると値が$-1$になることから２つ目の条件を満たさないため、良い組ではありません。

骨格

$Y$を基底とする自由$\mathbb{Z}$加群を$K$とし、$K$の元を骨格と呼ぶ。

つまり、非ゼロ整数の有限列$\{e_i\}_{i=1}^N$と良い組の有限列$\{(a_i,b_i,c_i)\}_{i=1}^N$を用いた
$$\sum_{i=1}^N e_i(a_i,b_i,c_i)$$
という形式和全体と単位元$0$を合わせ、この集合に加法で群としての構造を入れ、これを$K$と呼ぶ。

Kokkakuなので$K$です(カス)。
$$F=\sum_{i=1}^N e_i(a_i,b_i,c_i)$$という書き方をする場合、暗黙に$e_i\neq 0$が満たされているものとします。

骨格

$F=2(1,2,3)-1(2,0,-1)$
は骨格です。これに骨格
$G=3(1,2,3)+2(0,1,0)$
を足す演算をすると骨格$F+G=5(1,2,3)-1(2,0,-1)+2(0,1,0)$
が得られます。
$\pm 1(\cdots)$は$\pm(\cdots)$と略記するかもしれません。

ユニット、セル

$K$を定義域とする写像$\Omega$を
$$\Omega(0)=1$$
$$\Omega:\sum_{i=1}^{N} e_i(a_i,b_i,c_i)\mapsto \prod_{i=1}^{N} \left[(a_in+b_ik+c_i)!\right]^{e_i}$$
で定める。
$K$の$\Omega$による像を$U$と書き、$U$の元を「ユニット」と呼ぶ。
特に$[(an+bk+c)!]^e$と表されうるユニットを「セル」と呼ぶ。

Unitなので$U$です。

つまり…？

$$f=\prod_{i=1}^{N} \left[(a_in+b_ik+c_i)!\right]^{e_i}$$と表されうる、$n,k$(定義域は$n\geq k\geq 1$)の２変数関数$f$を「ユニット」と呼びます。
特に$N=1$で書ける場合をセルと呼びます。

良い組をギリシャ小文字$\alpha,\beta$など、骨格を英大文字$F,G$など、ユニットを英小文字$f,g$などで表します。また、ユニットの$n,k$に対する代入操作を考える場合は$f(n,k)$などと明示的に書きます。

ユニットと骨格の合同

ユニット$f$と$g$が下の条件を満たすとき、$f$と$g$は合同であるといい、$f \equiv g$と書く。

ある正整数$m,n$が存在して、$m\cdot f = n \cdot g$

骨格$F$と$G$が下の条件を満たすとき、$F$と$G$は合同であるといい、$F \equiv G$と書く。

$\Omega(F) \equiv \Omega(G)$

要するに定数倍を無視するという話です。

例

例えば、先に示したように
$$3\cdot(2n+2)!(3n+2)! = 2\cdot(2n+1)!(3n+3)!$$
であることから、ユニットとしては
$$(2n+2)!(3n+2)! \equiv (2n+1)!(3n+3)!$$
であり、骨格としては
$$(2,0,2)+(3,0,2)\equiv (2,0,1)+(3,0,3)$$
です。

この意味での$\equiv$は反射律、対称律、推移律を満たすことが簡単に分かります。つまり同値関係です。

問いを立てます。

ユニットの分解

写像$\Phi:U\rightarrow K$であって、任意のユニット$f,g$に対して

$f \equiv \Omega\left(\Phi(f)\right),\quad g \equiv \Omega\left(\Phi(g)\right)$
$f \equiv g \Leftrightarrow \Phi(f) = \Phi(g)$

を満たすものを探そう。

上の要請を満たす写像$\Phi$を「分解写像」と呼ぶことにしましょう。

要するに、「$K$を”$\equiv$”で割った同値類の代表元を定める」ことであり、「合同なユニットを判定する方法を見つける」ことです。

ユニットの骨格とユニットを厳しく区別する必要があったために、定義が複雑になってしまいました。

基本的な性質の整理

$\Phi$の構成を与える前にできる議論は一通り終わらせてしまいます。

(1)$Y$の整理

下の同値性が成り立ちます。

良い組の条件

$(a,b,c)$が良い組であることは、下の４条件と同値である。

$a \neq 0$ または$b \neq 0$
$a \geq 0$
$a + b \geq 0$
$a + b + c \geq 0$

良い組の条件

良い組ならば、$N$を十分に大きな整数として、
2. $(N,1)$
3. $(N,N)$
4. $(1,1)$
を$(n,k)$に代入しながら$an+bk+c\geq 0$となる条件を見ることで、2,3,4それぞれの条件の必要性が分かります。
また
$$an+bk+c=a(n-k)+(a+b)(k-1)+(a+b+c)$$
と書けば十分性も分かります。

(2)$U$の整理

ユニットの集合$U$は、通常の意味での積を演算として可換群を成します。
ユニット同士の積は記号を省略して$fg$などと書きます。

(3)$\Omega$の整理

ユニットの定義の式
$$f=\prod_{i=1}^{N} \left[(a_in+b_ik+c_i)!\right]^{e_i}$$
は正の有理数$r\neq 1$の素因数分解
$$r=\prod_{i=1}^N p_i^{e_i}$$
と形が同じです。
しかし、有理数の素因数分解は一意なのに対して、ユニットをセルの積に分解する方法は一般には一意ではないという相違点があります。

例

\begin{align} 2nk &= (2n)k = [(2n)!]^1[(2n-1)!]^{-1}[k!]^1[(k-1)!]^{-1} \\ &= n(2k) = [n!]^1[(n-1)!]^{-1}[(2k)!]^1[(2k-1)!]^{-1} \end{align}
（つまり頭の2を$n$と$k$のどちらに分配するのかによって変わってしまう）などが例となります。

つまり、$\Omega$は単射ではありません。複数の骨格が同一のユニットに対応する可能性があります。

$\Omega$について重要なのは、これが骨格からユニットへの全射な準同型であるという点です。

準同型写像$\Omega$

任意の骨格$F,G$について
$$\Omega(F+G)=\Omega(F)\Omega(G)$$

(4)合同$\equiv$の整理

ユニットの合同に関して下の性質が成り立ちます。$\equiv$の定義と上の定理より自明です。

$\equiv$の扱い

ユニット$f,g$が$f\equiv g$を満たすとき、任意のユニット$h$に対して
$$fh\equiv gh$$
が成立する。
骨格$F,G$が$F\equiv G$を満たすとき、任意の骨格$H$に対して
$$F+H\equiv G+H$$
が成立する。

(5)$\Phi$の整理

分解写像$\Phi$の要請を再掲します。

分解写像の要請

写像$\Phi:U\rightarrow K$であって、任意のユニット$f,g$に対して

$f \equiv \Omega\left(\Phi(f)\right),\quad g \equiv \Omega\left(\Phi(g)\right)$
$f \equiv g \Leftrightarrow \Phi(f) = \Phi(g)$

を満たすものを分解写像と呼ぶ。

分解写像の判定法

分解写像の要請1を満たす写像$P:U\rightarrow K$について、下の２命題は同値である。

$P$は分解写像の要請2を満たす
任意の骨格$F,G\in\mathrm{Im}~P$に対して、$F\equiv G$ならば$F=G$

分解写像の判定法

長いので畳む

((1)→(2))まず$P$が分解写像の要請1,2を満たすとする。
$F\equiv G$を満たす任意の骨格$F,G\in\mathrm{Im}~P$に対し、$\mathrm{Im}$の定義より
$P(f)=F,P(g)=G$
を満たすユニット$f,g$が存在する。
分解写像の要請の1つめより
ア $f\equiv\Omega(F)$
イ $g\equiv\Omega(G)$
だが、$F\equiv G$であったことを思い出し、さらに骨格の合同の定義は
ウ $\Omega(F)\equiv\Omega(G)$
であったことを思い出せば、アイウと合同の推移律より$f\equiv g$である。
分解写像の２つ目の要請より$P(f)=P(g)$つまり$F=G$である。

((2)→(1))次に、任意の骨格$F,G\in\mathrm{Im}~P$に対して、「$F\equiv G$ならば$F=G$」が成立しているとする。
I. $f\equiv g \rightarrow P(f)=P(g)$を示す。
$f\equiv g$とする。$P$は分解写像の要請1を満たすから
$f\equiv \Omega(P(f))$
$g\equiv \Omega(P(g))$
である。推移律より$\Omega(P(f))\equiv\Omega(P(g))$であり、これは骨格の合同の定義より$P(f)\equiv P(g)$を意味する。仮定より$P(f)=P(g)$となる。
II. $P(f)=P(g)\rightarrow f \equiv g$を示す。
$P(f)=P(g)$とする。両辺に$\Omega$を作用させ$\Omega(P(f))=\Omega(P(g))$である。$P$は分解写像の要請1を満たすから再び
$f\equiv \Omega(P(f))$
$g\equiv \Omega(P(g))$
であり、推移律より$f\equiv g$が言えた。

よって$P$が分解写像の要請2を満たすことが確認できた。

この「分解写像の判定法」が今回のメインウェポンです。

$\Phi$の準備

非ゼロ基底

骨格$F\neq 0$が
$$F=\sum_{i=1}^N e_i(a_i,b_i,c_i)$$
と書かれるとする。

「良い組$(a,b,c)$は$F$の非ゼロ基底である」とは、$(a,b,c)=(a_i,b_i,c_i)$となる$i$が存在することを言う。骨格$0$には非ゼロ基底は存在しないとする。
$F$の非ゼロ基底の集合を$Y(F)$と書く。$Y(F)$は有限集合であり、$Y(F)\subset Y$である。

成分

骨格$F\neq 0$が
$$F=\sum_{i=1}^N e_i(a_i,b_i,c_i)$$
と書かれるとする。

良い組$(a,b,c)$に対して「$F$の$(a,b,c)$成分」とは、

$(a,b,c)=(a_i,b_i,c_i)$となる$i$が存在すれば$e_i$
そうでなければ$0$

を指す。

良い組の既約

良い組$(a,b,c)$が以下の条件を満たすとき、$(a,b,c)$は既約であるという。

$a+b+c=0$または$\text{gcd}(a,b,c)=1$

ただし$\text{gcd}(a,b,c)$は$a,b,c$の最大公約数です。

詳しく$\Phi$の構成を述べる前に、次の章で構成する$\Phi$がどのように働くかを見てみましょう。ユニット$(6n+3)!$の分解は以下のように進みます。

\begin{align} (6n+3)! &= (6n+3)\cdot(6n+2)! \\ &= 3(2n+1)\cdot(6n+2)! \\ &\equiv (2n+1)\cdot(6n+2)! \\ &= \frac{(2n+1)!}{(2n)!}\cdot(6n+2)! \\ &= \frac{1}{2n}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot(6n+2)! \\ &\equiv \frac{1}{n}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot(6n+2)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot(6n+2)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot(6n+2)\cdot(6n+1)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot 2(3n+1)\cdot(6n+1)! \\ &\equiv \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot(3n+1)\cdot(6n+1)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot\frac{(3n+1)!}{(3n)!}\cdot(6n+1)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot\frac{1}{3n}\cdot\frac{(3n+1)!}{(3n-1)!}\cdot(6n+1)! \\ &\equiv \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot\frac{1}{n}\cdot\frac{(3n+1)!}{(3n-1)!}\cdot(6n+1)! \\ &= \frac{(n-1)!}{n!}\cdot\frac{(2n+1)!}{(2n-1)!}\cdot\frac{(n-1)!}{n!}\cdot\frac{(3n+1)!}{(3n-1)!}\cdot(6n+1)! \\ &= \frac{(6n+1)!(3n+1)!(2n+1)![(n-1)!]^2}{(3n-1)!(2n-1)![n!]^2} \end{align}

最終的に全てのセルの骨格が既約になるように、
$$\begin{aligned} &(gan+gbk+gc)! \\ &\equiv\frac{(an+bk+c)!}{(an+bk+c-1)!}(gan+gbk+gc-1)! \end{aligned}$$
を根拠とした変形を繰り返して手続きが進んでいきます。

$\Phi$の構成

分解手続き$\Phi$

ユニット$f$に対して、骨格$\Phi(f)$を下の手続きを実行した出力として定義する。
(説明が分かりにくい場合、こちら(wandbox) をご参照ください。処理2以降と大体同じことをC++で実行するプログラムです。)

$\Omega(F)=f$を満たす骨格$F$をひとつ取る。
$F=0$の場合は$0$を出力して終了する。
$F$の非ゼロ基底が全て既約ならば$F$を出力して終了する。
$F$の非ゼロ基底のうち既約でないものをひとつ選び$\alpha=(ga,gb,gc)$とする($g\geq 2,\gcd(a,b,c)=1$)。$F$の$\alpha$成分を$e$とする。
上の$\alpha=(ga,gb,gc)$を用いて
$$\alpha’_1\coloneqq(ga,gb,gc-1)$$
$$\alpha’_2\coloneqq(a,b,c)$$
$$\alpha’_3\coloneqq(a,b,c-1)$$
と定める。$F$を
$$F\leftarrow F-e\alpha+e\alpha’_1+e\alpha’_2-e\alpha’_3$$
と更新する。
2へ戻る。

諸々の正当性の確認をしましょう。

処理4の$\alpha’_1,\alpha’_2,\alpha’_3$が良い組である保証
手続きの停止性の保証
出力の一意性の保証

1.の証明は容易なので省略します。
2.を示す必要があるのは明らかでしょう。処理2~5のループを抜けられる保証が必要です。
3.については、手続き内に「骨格をひとつ取る」「非ゼロ基底のうち既約でないものをひとつ取る」という自由度が存在することによります。選び方によらず出力がひとつに定まることを言わなければなりません。その一意性を示すのがこの記事の主題です。

手続き$\Phi$の停止性

良い組$\beta=(a,b,c)$に対して
$$\text{sum}(\beta)=a+b+c$$
として$\text{sum}$を定義する。
少し計算すれば、処理4の$\alpha,\alpha’_1,\alpha’_2,\alpha’_3$について
$$\text{sum}(\alpha)-1\geq\text{sum}(\alpha’_1),\text{sum}(\alpha’_2),\text{sum}(\alpha’_3)\geq 0$$
となっていることが分かる。$F$の更新後に$F$の$\alpha$成分が$0$になること、$\text{sum}$に下限$0$が存在することを踏まえると、操作は有限回で停止する。

とりあえず、$\Phi$にユニットを突っ込むと、(途中の選び方によって違う結果になるかもしれないとはいえ)なんらかの骨格が出力されるということは、最低限保証できました。

下は割と重要な主張です。

出力の性質

ユニット$f$を$\Phi$に通した出力として骨格$F$が得られたとする。この時$$\Omega(F)\equiv f$$

出力の性質

処理4において、
$$\begin{aligned} & \Omega(F-e\alpha+e\alpha’_1+e\alpha’_2-e\alpha’_3) \\ &=\Omega(F)\frac{\Omega(e\alpha’_1)\Omega(e\alpha’_2)}{\Omega(e\alpha)\Omega(e\alpha’_3)} \\ &=\Omega(F)\frac{[(gan+gbk+gc-1)!]^e[(an+bk+c)!]^e}{[(gan+gbk+gc)!]^e[(an+bk+c-1)!]^e} \\ &=\Omega(F)\frac{1}{g^e} \\ &\equiv \Omega(F) \end{aligned}$$
より、各更新ごとに更新前の骨格と更新後の骨格は合同であり、はじめ$\Omega(F)=f$だったことと合わせれば分かる。

$\Phi$の出力の一意性保証

(1)$K_{PF}$について

定義

集合$K_{PF}$

集合$K_{PF}\subset K$を下のように定義する。ただし$0\in K_{PF}$であるとする。
$$K_{PF}=\left\lbrace\sum_{i=1}^{N} e_i(a_i,b_i,c_i)\in K\middle|(a_i,b_i,c_i)\text{は全て既約}\right\rbrace$$
$K_{PF}$の元を既約骨格と呼ぶ。

つまり「非ゼロ基底が全て既約な骨格」を既約骨格と呼びます。

$K_{PF}$の${}_{PF}$は$\mathrm{Prime}~\mathrm{Factorization}$です。
既約な良い組と素数には類似性があり、$K_{PF}$の元(既約骨格)はある意味で素因数分解されたような形になっています。

$K_{PF}$の対外的な立ち位置

実は「$\Phi$からの出力としてありうる骨格全ての集合」は$K_{PF}$と等しいことが言えます。

演習:なぜ？

出力としてありうる骨格全ての集合を$A$とおく。まず$\Phi$の出力として得られる骨格に属する良い組は必ず既約になっているから$A\subset K_{PF}$が成立する。
次に$K_{PF}$に属する骨格$F$を取ってくる。$\Omega(F)$を$\Phi$に突っ込み、処理1で骨格として$F$を選べば、処理2ですぐに$F$そのものが出力される。つまり$A\supset K_{PF}$も成立し、結局$A=K_{PF}$である。

$K_{PF}$自体の構造

$K_{PF}$は$K$の部分加群になります。確認は容易です。

(2)問題の整理

メインウェポン「分解写像の判定法」について、「考えている手続きがそもそも写像と言えるかどうかすら分からない」という現状に合わせて議論しなおします。

結局の問題

任意の$F,G\in K_{PF}$に対し、$F \equiv G \rightarrow F=G$

命題7の重要性

命題7が成立するならば、$\Phi$は分解写像である。

命題7の重要性

ユニット$f$を$\Phi$に通した結果、手続き途中の選び方を変えたことで異なる$F,G$の2種類の骨格が出力されたとする。出力の性質より$f\equiv\Omega(F)\equiv\Omega(G)$であり、これは定義通り$F\equiv G$を意味する。命題7の仮定より$F=G$となる。

出力の一意性が保証されたので$\Phi(f)$という書き方ができる。これを使って出力の性質を書き直すと$f\equiv\Omega(\Phi(f))$であり、これは分解写像の要請1そのものである。
以上と「分解写像の判定法」より$\Phi$は分解写像となる。

以上より、既約骨格$K_{PF}$に関する命題である命題7さえ証明できれば良いことが分かります。問題を手続き$\Phi$から分離できました。

(3)議論する対象の拡張

さて、命題7の証明は、$\Phi$による分解よりもう一度「深い」分解$\Phi’$を考えることで行います。$\Phi$による分解を整数の素因数分解に例えるなら、$\Phi’$による分解はガウス整数環での素因数分解に例えられます。

この分解はユニットを関数として見た時の$n,k$の定義域を犠牲にします。この辺りは厳密に述べようとするとほとんど繰り返しになってしまうので概略のみ示します。これは論文ではないので…

悪くない組

下の４条件を満たす整数３つの順序組$(a,b,c)$を「悪くない組」と呼ぶ。

$a \neq 0$または$b \neq 0$
$a \geq 0$
$a+b \geq 0$
$a+b+c \geq -1$

悪くない組の集合を$Y’$とする。

「良い組」の条件を緩めたものになっており、$Y\subset Y’$が成立します。

悪くない組の性質

$(a,b,c)$が悪くない組であるとき、下の性質が成り立つ。

$n-1 \geq k \geq 2$ならば$an+bk+c \geq 0$

$a=0$のとき、$b\geq 1,b+c\geq -1$なので、
$$an+bk+c = b(k-2)+b+(b+c)$$
と書けば分かる。
$a\geq 1$のとき、
$$an+bk+c=a(n-1-k)+(a+b)(k-1)+a+(a+b+c)$$
と書けば分かる。

これに伴い、悪くない組を組み込んだ骨格を定義します。

擬骨格、擬ユニット、擬セル

$Y’$を基底とする自由$\mathbb{Z}$加群を$K’$と書き、$K’$の元を擬骨格と呼ぶ。

$\Omega$の定義域を擬骨格まで自然に広げ、$K’$の$\Omega$による像を$U’$と書き、$U’$の元を擬ユニットと呼ぶ。

悪くない組$(a,b,c)$と整数$e\neq 0$により
$$\alpha=[(an+bk+c)!]^e$$
と表されうる擬ユニット$\alpha$を特に擬セルと呼ぶ。

$(2n+3k-1)!$はセルですが、擬セルでもあります。$(2n+3k-6)!$はセルではありませんが、擬セルです($2+3+(-6)=-1$だから)。
一般に
(概念)$\subset$擬(概念)
(集合)$\subset$(集合)’
となっています。
これに伴い、骨格の合同の定義を擬骨格・擬ユニットまで自然に広げておきます。

悪くない組の完全既約

悪くない組$\alpha=(a,b,c)$が以下の条件を満たすとき、$\alpha$は完全既約であるという。

$\text{gcd}(a,b,c)=1$

特に、$a+b+c=-1$のとき必ず$\gcd(a,b,c)=1$となるため、「よい組でない悪くない組」は必ず完全既約です。

集合$K’_{PF}$

集合$K’_{PF}\subset K’$を下のように定義する。ただし$0\in K’_{PF}$であるとする。
$$K’_{PF}=\left\lbrace\sum_{i=1}^{N} e_i(a_i,b_i,c_i)\in K’\middle|(a_i,b_i,c_i)\text{は全て完全既約}\right\rbrace$$
$K’_{PF}$の元を完全既約擬骨格と呼ぶ。

下のような包含関係が成り立ちます。

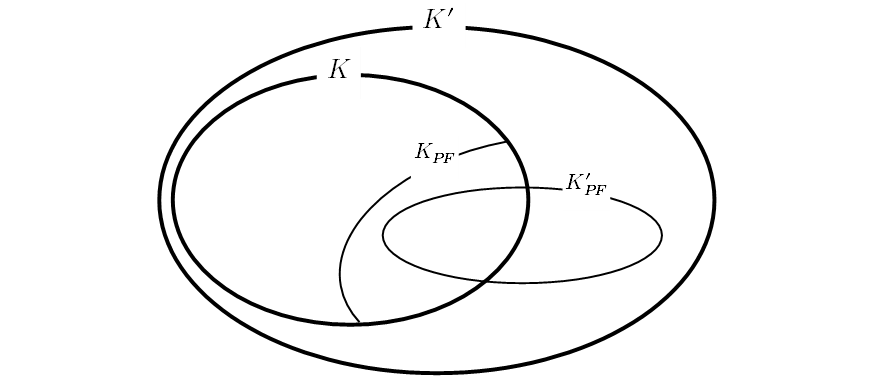包含関係

整数としては素数だがより大きなガウス整数のなかでは素数として振る舞わないものがあること、及び通常の意味での素数ではないがガウス素数であるものが存在すること、によく似ています。

記号は適当に察して

考える対象をユニットから擬ユニットにまで広げ、それに伴い既約と呼ぶ条件を厳しくして($a+b+c=0$を削除して)います。

(4)$K_{PF},K’_{PF}$の構造

$K_{PF}\cup K’_{PF}$から生成される加群を$\langle K_{PF}\cup K’_{PF} \rangle$と書くことにします。
これは以下のように４つの部分加群の直和に分解することができます。

$\langle K_{PF}\cup K’_{PF}\rangle$の直和分解

$$\langle K_{PF}\cup K’_{PF}\rangle=K’_1\oplus K’_2\oplus K’_3\oplus K’_4$$
ただし
$$K’_1\coloneqq \left\lbrace F\in K_{PF}~~\middle|~~ \begin{aligned} &\forall(a,b,c)\in Y(F): \\ &\gcd(a,b,c)\geq 2\land a+b+c=0 \end{aligned} \right\rbrace\cup\{0\}$$
$$K’_2\coloneqq \left\lbrace F\in K_{PF}~~\middle|~~ \begin{aligned} &\forall(a,b,c)\in Y(F): \\ &\gcd(a,b,c)= 1\land a+b+c\geq 0 \end{aligned} \right\rbrace\cup\{0\}$$
$$K’_3\coloneqq \left\lbrace F\in K’_{PF}~~\middle|~~ \begin{aligned} &\forall(a,b,c)\in Y(F): \\ &\gcd(a,b)\geq 2\land a+b+c=-1 \end{aligned} \right\rbrace\cup\{0\}$$
$$K’_4\coloneqq \left\lbrace F\in K’_{PF}~~\middle|~~ \begin{aligned} &\forall(a,b,c)\in Y(F): \\ &\gcd(a,b)= 1\land a+b+c=-1 \end{aligned} \right\rbrace\cup\{0\}$$

既約な良い組が$K’_1,K’_2$の、完全既約な悪くない組が$K’_3,K’_4$の2行目の条件のうちいずれか１つのみを満たすことから明らかだと思います。

(5)$\Phi’$の構成

$\Phi’$の定義域は$K_{PF}$です。$\Phi$がユニットから既約骨格への写像だったのに対し、$\Phi’$は既約骨格から完全既約擬骨格への写像です。

完全分解手続き$\Phi’$

既約骨格$F\in K_{PF}$に対して、$\Phi’(F)$を下の手続きを実行した出力として定義する。

$F=F_1+F_2+F_3+F_4$と分割する。ただし前の章の直和分解を用いて$F_i\in K’_i$となるように取る。よってはじめ$F_3=F_4=0$である。
$F_1=0$ならば$F_2+F_3+F_4$を出力して終了する。
$F_1$の非ゼロ基底をひとつ選び、$(ga,gb,-ga-gb)$とする($g\geq 2,\gcd(a,b)=1$)。$F_1$の$(ga,gb,-ga-gb)$成分を$e$とする。
上の$(ga,gb,-ga-gb)$を用いて
$$F_1\leftarrow F_1-e(ga,gb,-ga-gb)$$
$$F_2\leftarrow F_2+e(a,b,-a-b)$$
$$F_3\leftarrow F_3+e(ga,gb,-ga-gb-1)$$
$$F_4\leftarrow F_4-e(a,b,-a-b-1)$$
と更新する。この更新前後で$F_i\in K’_i$という性質は保たれる。
処理2に戻る。

停止保証はいいでしょう(ループごとに$F_1$の非ゼロ基底がひとつずつ減る)。
出力の一意性については、$\Phi$と異なり$\Phi’$は引数として明示的に骨格を取る点、$F_1$に新たな非ゼロ基底が生まれることがない点、加法に結合法則が成り立つ点より、「$F_1$の非ゼロ基底全てに対して一気に一度だけ操作を行う」としても良いので大丈夫でしょう。

$\Phi’$には下の重要な性質があります。

$\Phi’$の性質1

$F\in K_{PF}$について、$F\neq 0$ならば$\Phi’(F)\neq 0$
(ほぼ同じことだが)$\mathrm{Ker}~\Phi’=\{0\}$

これの証明のため補題を１つ用意します。

$F_3$を用意した意味

処理4の更新により、$F_3$の非ゼロ基底数は必ず$1$増える。

$F_3$を用意した意味

長いので畳む

あるループにおいて、処理3で$F_1$の非ゼロ基底として$(ga,gb,-ga-gb)$が選ばれ、処理4で
$$F_3\leftarrow F_3+e(ga,gb,-ga-gb-1)$$
という更新が行われたとする。この更新前の$F_3$の$(ga,gb,-ga-gb-1)$成分が$0$であることを示せば良い。
更新前の$F_3$の$(ga,gb,-ga-gb-1)$成分が$0$でなかったと仮定する。手続き$\Phi’$開始時には$F_3=0$であったから、どこかのループの処理3で$F_1$から$F_1$の非ゼロ基底として$(ga,gb,-ga-gb)$が選ばれたことになるが、そのループの処理4での更新後に$F_1$の$(ga,gb,-ga-gb)$成分は$0$になったはずであり、今回$(ga,gb,-ga-gb)$が$F_1$の非ゼロ基底として選ばれたことと矛盾する。

補題を用いて証明します。

$\mathrm{Ker}~\Phi’=\{0\}$

$\Phi’(0)=0$はよい。
骨格$F\neq 0$に$\Phi’$を適用する。処理1の終了時点で$F_1$と$F_2$のいずれかは$0$でない。
$F_1$が$0$である場合、処理2で即座に$F_2$が出力され、このとき$F_2$は$0$でないままなので良い。
$F_1$が$0$でない場合は処理4が少なくとも$1$回行われ、上の補題より出力時の$F_3$の非ゼロ基底数は$1$以上である。
よってどちらの場合でも$F_1+F_2+F_3$は$0$ではない。

標語的には、「$\Phi$によって$0$まで潰れないなら、$\Phi’$によっても$0$まで潰れない」と言えるでしょう。

また下も成立します。証明は$\Phi$の時と全く同様なので省略します。

$\Phi’$の性質2

$F \in K_{PF}$に対して、$F\equiv\Phi’(F)$

$(2n-2)!$(既約なセル)を、完全既約な擬セルの積に分解してみます。$\Phi$ではこれ以上分解されませんが、$\Phi’$はさらに分解します。

\begin{align} (2n-2)! &= (2n-2)\cdot(2n-3)! \\ &= 2(n-1)\cdot(2n-3)! \\ &\equiv (n-1)\cdot(2n-3)! \\ &= \frac{(n-1)!}{(n-2)!}\cdot(2n-3)! \\ &= \frac{(2n-3)!(n-1)!}{(n-2)!} \end{align}

$\Phi’$による分解により、$n=1$を代入できなくなっています。これが「ユニットの定義域を犠牲にする」の意味です。

実は$\Phi’$は単射な準同型であり、$K_{PF}\cong \mathrm{Im}~\Phi’$が成立するのですが、この事実は使わないので詳しくは述べません。

(6)命題7の証明

ディリクレの算術級数定理

互いに素な正整数の組$a,b$に対し、$an+b$($n$は正整数)の形で書ける素数は無限に存在する。

ここから牛刀の極み（ディリクレの算術級数定理）をやりすぎなほど用いて、鶏（命題7）を割いて（証明して）いきます。

まず補題を示します。

本質部分

$N\geq 2$とする。完全既約擬骨格$F$が
$$F=\sum_{i=1}^{N} e_i(a_i,b_i,c_i)$$
と書かれているとする。ただし、非ゼロ基底を並び替えることで、任意の$2\leq i\leq N$に対して

$a_1>a_i$
$a_1=a_i$かつ$b_1>b_i$
$a_1=a_i$かつ$b_1=b_i$かつ$c_1>c_i$

のいずれかが成立するようにしておく。
この時、以下の条件を満たす素数$p$は無限に存在する。

ある整数$n,k$が存在し、下の2条件を満たす。
1. 任意の$2\leq i\leq N$に対し$a_1n+b_1k+c_1>a_in+b_ik+c_i\geq 0$
2. $p=a_1n+b_1k+c_1$

割と本質情報を沢山使うのでここが証明の本体です。

補題17

まず$i$ごとに$(a_1-a_i)n+(b_1-b_i)k+(c_1-c_i)>0$が成立する$n,k$の集合がどのようであるかを示し、それらの共通部分を取る。
①$a_1=a_i$かつ$b_1=b_i$のとき
$c_1>c_i$が成立する。よって任意の$n,k$で成立する。
②$a_1=a_i$かつ$b_1>b_i$のとき
$k>-\dfrac{c_1-c_i}{b_1-b_i}$で成立する。$n$は任意。
③$a_1>a_i$のとき
任意の$k$に対し、$n>-\dfrac{(b_1-b_i)k+(c_1-c_i)}{a_1-a_i}$で成立する。

②のパターンの$i$全てにわたって$k$の下限値$-\dfrac{c_1-c_i}{b_1-b_i}$を計算し、これの最大値と$1$のうち大きい方に$1$を足したものを$k_{\min}$とする。ただし②のパターンの$i$が存在しない場合、$k_{\min}=2$とする。
さらに、$k$を決めた上で③のパターンの$i$全てにわたって$n$の下限値$-\dfrac{(b_1-b_i)k+(c_1-c_i)}{a_1-a_i}$を計算し、これの最大値と$k$のうち大きい方に$1$を足したものを$n_{\min}(k)$とする。ただし③のパターンの$i$が存在しない場合、$n_{\min}(k)=k+1$とする。
$k\geq k_{\min}$を満たす任意の$k$に対して、$n\geq n_{\min}(k)$を満たす$n$で(1)の条件が満たされることがわかった。
この範囲の$n,k$によって$a_1n+b_1k+c_1$と書ける素数が無限にあることを示せば良い。

$a_1=0$の場合、$b_1\geq 1$であり、かつ$F$が完全既約擬骨格であることより$\gcd(b_1,c_1)=1$である。ここでインドラの矢（ディリクレの算術級数定理）を用いると、$b_1k+c_1$の形で書ける素数は無限に存在することがわかり、有限個を除いた$k\geq k_{\min}$の範囲にも素数が無限に存在する。

$a_1\geq 1$の場合、$\gcd(a_1,b_1,c_1)=1$より、$\gcd(a_1,b_1k+c_1)=1$となる$k$が$k\geq k_{\min}$の範囲に存在する。

簡単な証明法があったら教えてください

$b_1=0$の場合、$\gcd(a_1,c_1)=1$より任意の$k$が条件を満たす。
$b_1\neq 0$の場合、$g\coloneqq\gcd(b_1,c_1)$と置き$b_1=gb',c_1=gc'$とする。ここでニワトコの杖（ディリクレの算術級数定理）を使えば、$|b'k+c'|$は無限に多くの、特に$a_1$より大きな素数の値を取り得る。このとき$a_1$と$b_1k+c_1=g(b'k+c')$は互いに素である。

この$k$で固定して、$n$を動かす形でもはや冒涜（ディリクレの算術級数定理）を用いれば$a_1n+b_1k+c_1$の形で書ける素数は無限に存在し、有限個を除いた$n\geq n_{\min}(k)$の範囲にも素数が無限に存在する。

本筋に入ります。

命題7の証明

$F,G\in K_{PF}$が、$F\neq G$かつ$F\equiv G$を満たしているとする。
$F \equiv G$より
$$F-G\equiv G-G=0$$
である。$K_{PF}$は加群なので$F-G\in K_{PF}$である。よって$\Phi’(F-G)$が定義され、$\Phi’$の性質2から
$$\Phi’(F-G)\equiv F-G\equiv 0$$
合同の定義より$\Omega(\Phi’(F-G))\equiv \Omega(0)=1$である。
$F\neq G$より$F-G\neq 0$であり、$\Phi’$の性質1より$\Phi’(F-G)\neq 0$であるから
$$H\coloneqq\Phi’(F-G)=\sum_{i=1}^{N} e_i(a_i,b_i,c_i)$$とおけ、さらに$$f(n,k)\coloneqq\Omega(H)=\prod_{i=1}^{N}[(a_in+b_ik+c_i)!]^{e_i}$$とおける。
$$\begin{aligned} f&=\Omega(H) \\ &=\Omega(\Phi’(F-G)) \\ &\equiv 1 \end{aligned}$$
であり、ユニットの合同の定義から、ある整数$s,t$が存在して
$$f(n,k)=\frac{s}{t}$$
が成立している。
$N=1$のとき、$f(n,k)=[(a_in+b_ik+c_i)!]^{e_i}$は$(a,b,c)$が悪くない組であることを使えば明らかに定数にならない。
$N\geq 2$とする。
$$f(n,k)=[(a_1n+b_1k+c_1)!]^{e_1}\prod_{i=2}^{N}[(a_in+b_ik+c_i)!]^{e_i}=\frac{s}{t}$$
補題17より、$f(n,k)$の定義域内において、$\prod_{i=2}^N[(a_in+b_ik+c_i)!]^{e_i}$の部分が$(a_1n+b_1k+c_1)$より小さな整数の積になるようにした上で、$(a_1n+b_1k+c_1)$が無限に多くの素数$p$の値を取ることができる。
これは$e_1>0$ならば$s$、$e_1<0$ならば$t$を割り切る素数が無限に存在することを意味し、矛盾である。