楕円曲線の集まりが，再び楕円曲線になる

楕円曲線の集合を考えると，その集合自体もまた楕円曲線とみなせる，という話について書きます．基本的にこの記事は三枝洋一先生の『数論幾何入門』1を参考にしています．この本は易しく，数論幾何に入門するのにとても良い本だと思うのでその方面に興味のある人はぜひ読んでみてください．

準備

楕円曲線とは

この記事で楕円曲線とは，ある$a_0,a_1,a_2\in \mathbb{C}$を用いて$y^2=x^3+a_2x^2+a_1x+a_0$という形の式で定義される$\mathbb{C}^2$の部分集合

$E=\{(x,y)\in \mathbb{C}^2 \mid y^2=x^3+a_2x^2+a_1x+a_0\}$

のこととします．

ただし，$y=0$として得られる$x$の方程式

$0=x^3+a_2x^2+a_1x+a_0$

が$\mathbb{C}$の範囲で重根を持たないという条件を課すことにします．(重根を持つ場合は楕円曲線に含めないことにします．)より広い，あるいはより正確な定義は1定義3.13を見てください．

また，この$E$を単に

$E:y^2=x^3+a_2x^2+a_1x+a_0$

とも書くことにします．

楕円曲線の例

この記事で主役になるのは，次の楕円曲線$\mathfrak{E}$です：

集合としては次の通りです：

ちなみに$\mathfrak{E}$はドイツ文字の$E$です．便宜のため，$\mathfrak{E}$の元は$(s,t)$で表すことにします．

$\mathfrak{E}$のグラフは次のようになっています：
楕円曲線$\mathfrak{E}$

ただし，$s,t$が実数であるような点$(s,t)$を表示しています．また，グラフを描画する際の都合で$s$軸に近いところでグラフが途切れてしまっていますが，本当はつながっています．以降で掲載するグラフについても同様です．(Elliptic Curveとは楕円曲線のことです．)

楕円曲線の集まりを考える

次のような，楕円曲線と付加的な情報の組の集合$M_{11}$を考えます．ただし，座標変換で移り合う楕円曲線は同じものとみなします：

以下では組$(E,P)$の同型類のことも単に$(E,P)$と書くことにします．

$11$等分点について軽く説明しておきましょう．まず，$E$を楕円曲線とするとき，$E$はある演算によって可換群になっています．$P\in E$であって群$E$における位数が$11$であるような点を$11$等分点と呼びます．

$M_{11}$においては，楕円曲線が同じ(同型)でも，組となっている$11$等分点$P$が異なれば，別のものと考えます．

ここで，さっき定義した$\mathfrak{E}$は$1$つの楕円曲線であるのに対し，$M_{11}$は全ての楕円曲線($+$付加情報の組)を集めたものであることに注意しておきます．
$\mathfrak{E}$の元は関係式$t^2=s^3-\dfrac{1}{3}s+\dfrac{19}{108}$を満たす複素数$s,t$の組$(s,t)$であり，$M_{11}$の元は楕円曲線$E$とその$11$等分点$P$の組$(E,P)$です．

$\mathfrak{E}$と$M_{11}$の対応

対応

この記事の目的は，$\mathfrak{E}$と$M_{11}$の間によい対応があることを見ることです．$\mathfrak{E}$と$M_{11}$の間に全単射があればよかったのですが，実はそうはならず，$\mathfrak{E}$からある$9$個の点を除外しなければなりません．それらの除外点を$Q_1,...,Q_9\in\mathfrak{E}$とおきます．あとで出てくる$1$点だけ，およその座標を明かしておきます($\approx$はニアリーイコールです)：

$Q_1\approx (-0.57443,0.42173)$

$Q_1$はグラフのここ(バツ印で表示)にあります：
除外点$Q_1$

では楕円曲線$\mathfrak{E}$のそれぞれの点にどんな楕円曲線が対応するかみてみましょう！次の写像が全単射になります：

(詳しくは，1,6.3節．)

ここで，$b,c\in\mathbb{C}$に対して楕円曲線$E(b,c)$とは，

のことです．(1の$E(b,c)$とは定義が異なるので注意してください．この記事における$E(b,c)$は1,p.105の$E(b,c)$を$y^2=x^3+...$という形に直したものになっています．)

また，$b(s,t),c(s,t)$の定義は次の通りです：

結局$\psi$は，楕円曲線$\mathfrak{E}$の点$(s,t)\in \mathfrak{E}\setminus\{Q_1,...,Q_9\}$に対し，楕円曲線$E(b(s,t),c(s,t))$とその$11$等分点$(0,-b(s,t)/2)$の組を対応させる写像です．

除外点があることを大目に見れば，この全単射$\psi$により$M_{11}=\mathfrak{E}$だと思えます．

これは「全ての楕円曲線が入っている箱を考えたら，その箱自体も楕円曲線だった！」というような状況ですね．(大雑把な言い方ですが，)$1$つの楕円曲線$\mathfrak{E}$に全ての楕円曲線が含まれているというのは，不思議な感じがします．

$\mathfrak{E}\in \mathfrak{E}$

さて，ということは，

という疑問がありうると思います．この疑問を正確に書くと，次のような命題になります．

この命題は成立します．実は楕円曲線は$11$等分点を必ず持つので，$\mathfrak{E}$の$11$等分点(の$1$つ)を$P$とし，$(s,t):=\psi^{-1}(\mathfrak{E},P)$とおけばよいです．($\psi$は全単射であることに注意．)

しかし，「では$s,t,P$は具体的には何か」というと，それは簡単には求まりそうにないので，求めません．実は$P$さえわかればあとは簡単な計算で$(s,t)$を求めることができるのですが，$P$を求めるには高次の方程式を解かないといけなさそうなので，諦めました．

でも理論上は，箱の中にその箱自身が入っていることになるのは，面白いですね．

対応の例

$\psi$による対応の例を$1$つ見てみましょう．

$\mathfrak{E}$の元$(s,t)=(2,2.740...)\in\mathfrak{E}$を考えます．
計算により，$b=b(s,t)\approx 14.229,\quad c=c(s,t)\approx 4.391$なので，楕円曲線$E=E(b,c)$の方程式はおよそ次の通りです：

また，$11$等分点$P$の座標はおよそ$P=(0,−7.115)$です．
$\psi(s,t)=(E,P)$が求まりました．$E$のグラフと点$P$の位置は次の通りです：
$E$のグラフと点$P$
オレンジ色の点が$P$です．

楕円曲線の連続的な変化を見よう

いくつかの点に対応する楕円曲線

$\mathfrak{E}$の点をいくつかとり，対応する楕円曲線のグラフを見てみましょう．

$\mathfrak{E}$のグラフとその上の点たち

青色で表示した点$(s,t)\in\mathfrak{E}$たちに対応するグラフを表示します．$s$座標が小さい点から順に表示します：

$s=-0.6$
$s=-0.4$
$s=-0.2$
$s=0.0$
$s=0.2$
$s=0.4$
$s=0.6$
$s=0.8$
$s=1.0$

ただし，オレンジ色の点は組になっている$11$等分点を表します．

グラフの形が連続的に変化していることが見て取れると思います．これは関数$b(s,t),c(s,t)$が$(s,t)$に関して連続だからですね．

楕円曲線の知識がある人は次のような疑問を持つかもしれません：

確かに，一見するとこれらのほとんどのグラフは特異点(おおよそ，曲線が交わっている点のこと)を持つように見えます．しかし，グラフを拡大してみると実は特異点がないことがわかります．例えば$(0.0,\sqrt{19/108})\in \mathfrak{E}$に対応する楕円曲線(図8)は拡大すると以下のようなグラフになっており，曲線は交わっておらず，特異点がないことがわかります：
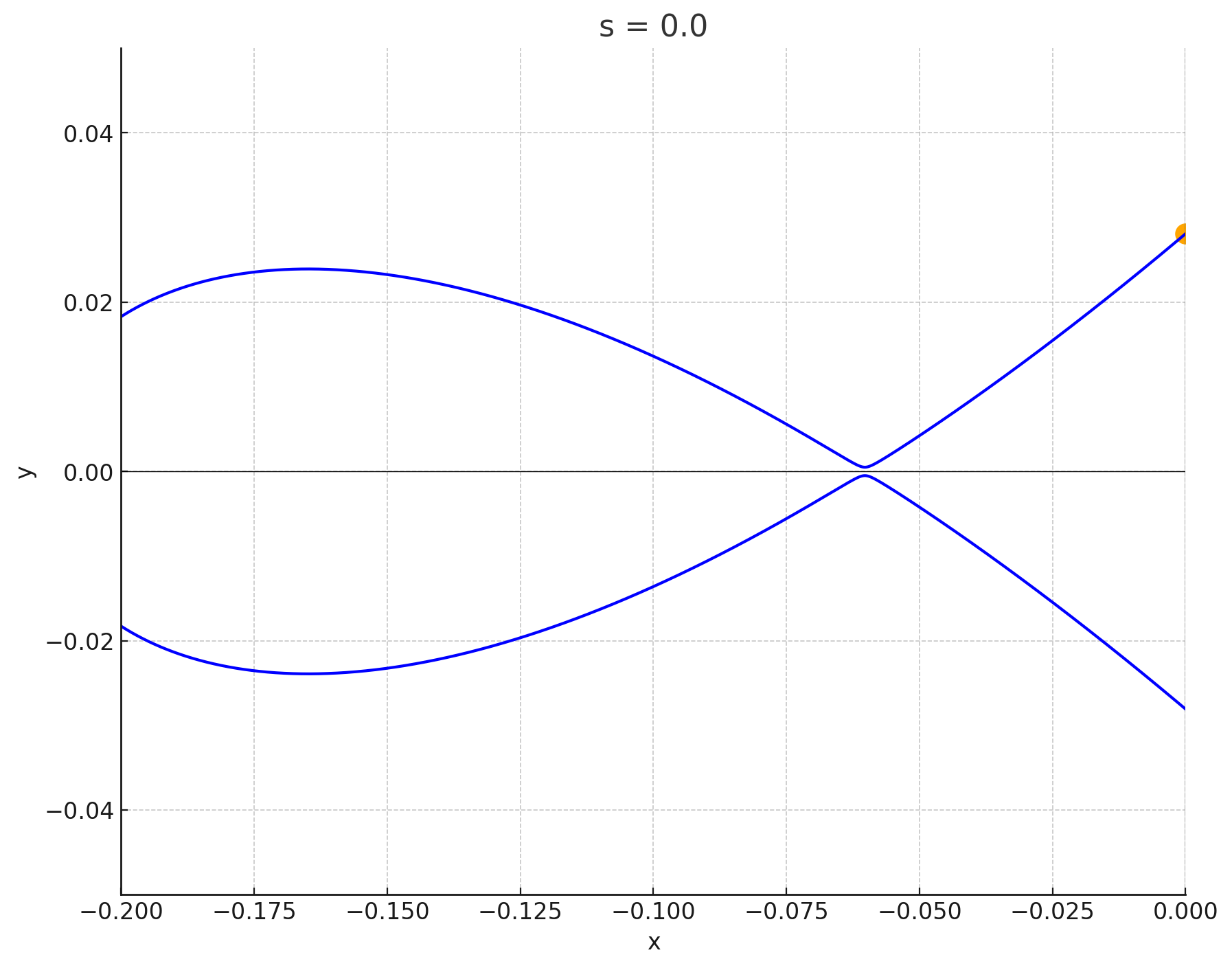拡大したもの
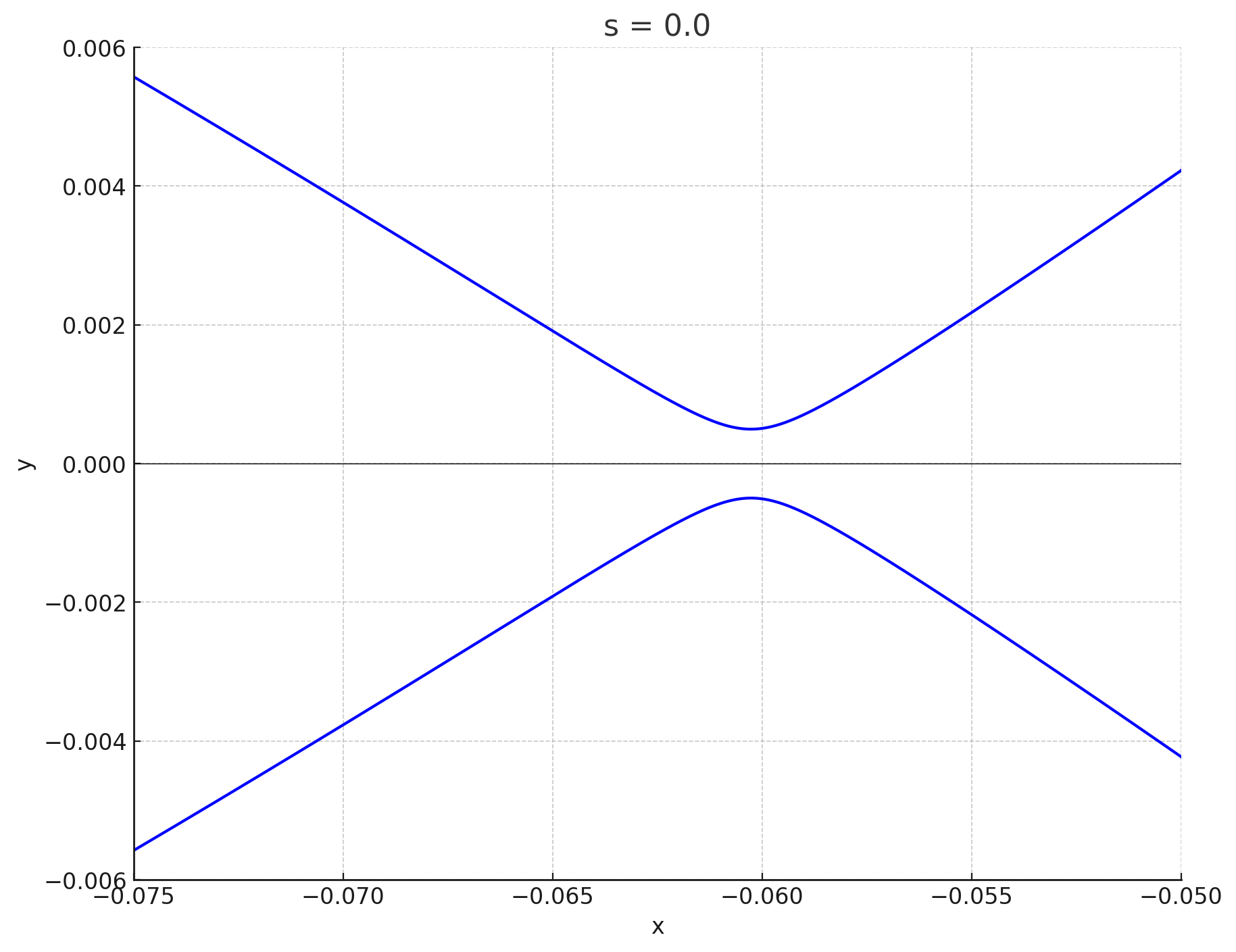もっと拡大したもの

グラフの変化の境界にあるもの

さて，図5,6,7,8,9を比較すると，図5だけ形が違う感じがします．$(s,t)\in\mathfrak{E}$に関して対応する楕円曲線のグラフが連続的に変化することを考えると，図5($s=-0.6$)と図6($s=-0.4$)との間がどうなっているのかが気になります．どこまでが図5のようなタイプのグラフで，どこからが図6のようなタイプのグラフになるのでしょうか？そして，ちょうど境界に位置するグラフはどうなっているのでしょうか？

私は答えを知っているので，すごく天下り的ですが$s=-0.5750$から$-0.5740$までの$6$個の点$(s,t)\in \mathfrak{E}\;(t>0)$に対応する楕円曲線のグラフを見てみましょう．次の図で青色で表示した$6$個の点に対して，対応する楕円曲線を考えることにします：
$\mathfrak{E}$上の6点

対応する楕円曲線のグラフを表示します．$s$座標が小さい点から順に表示します：
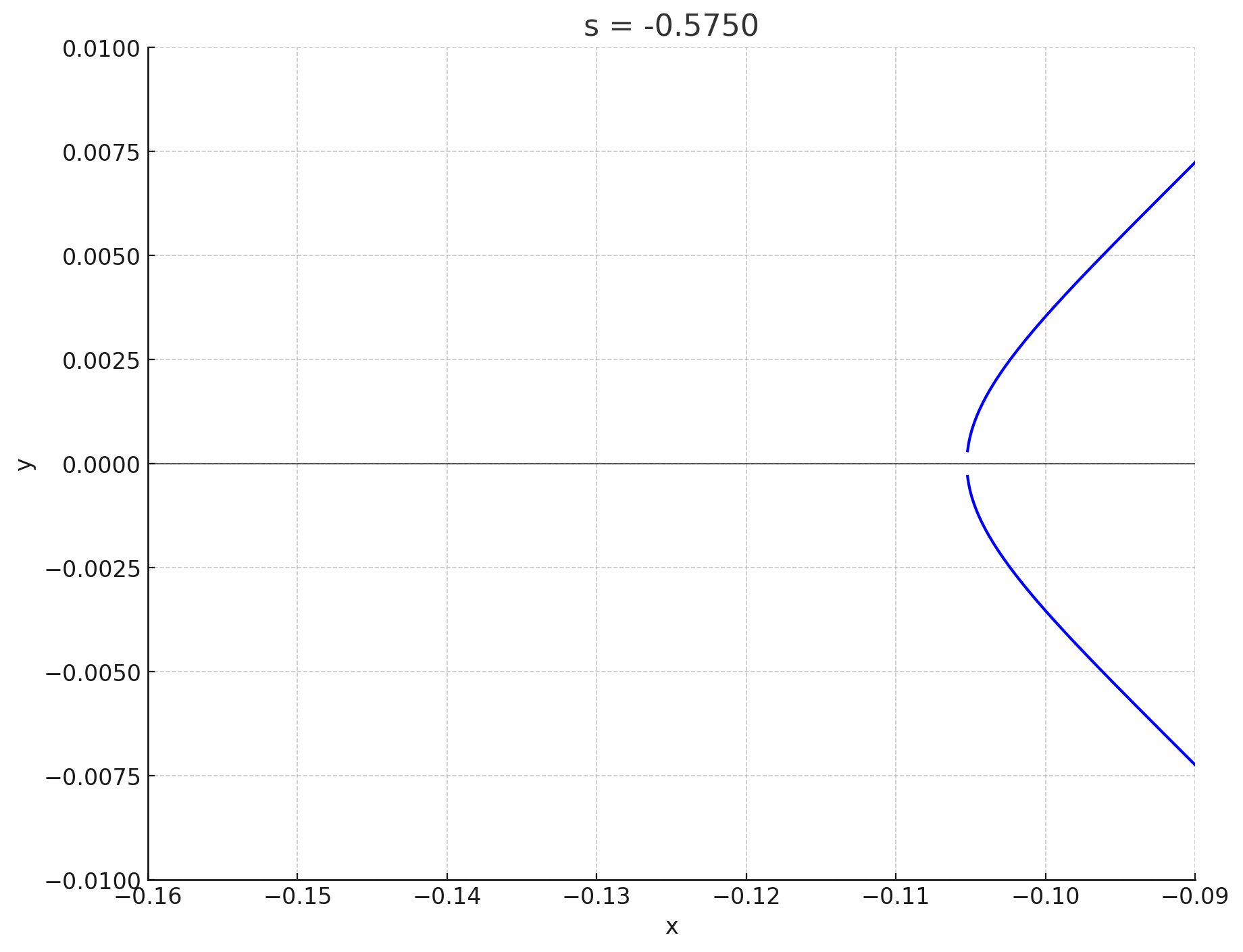s=-0.5750
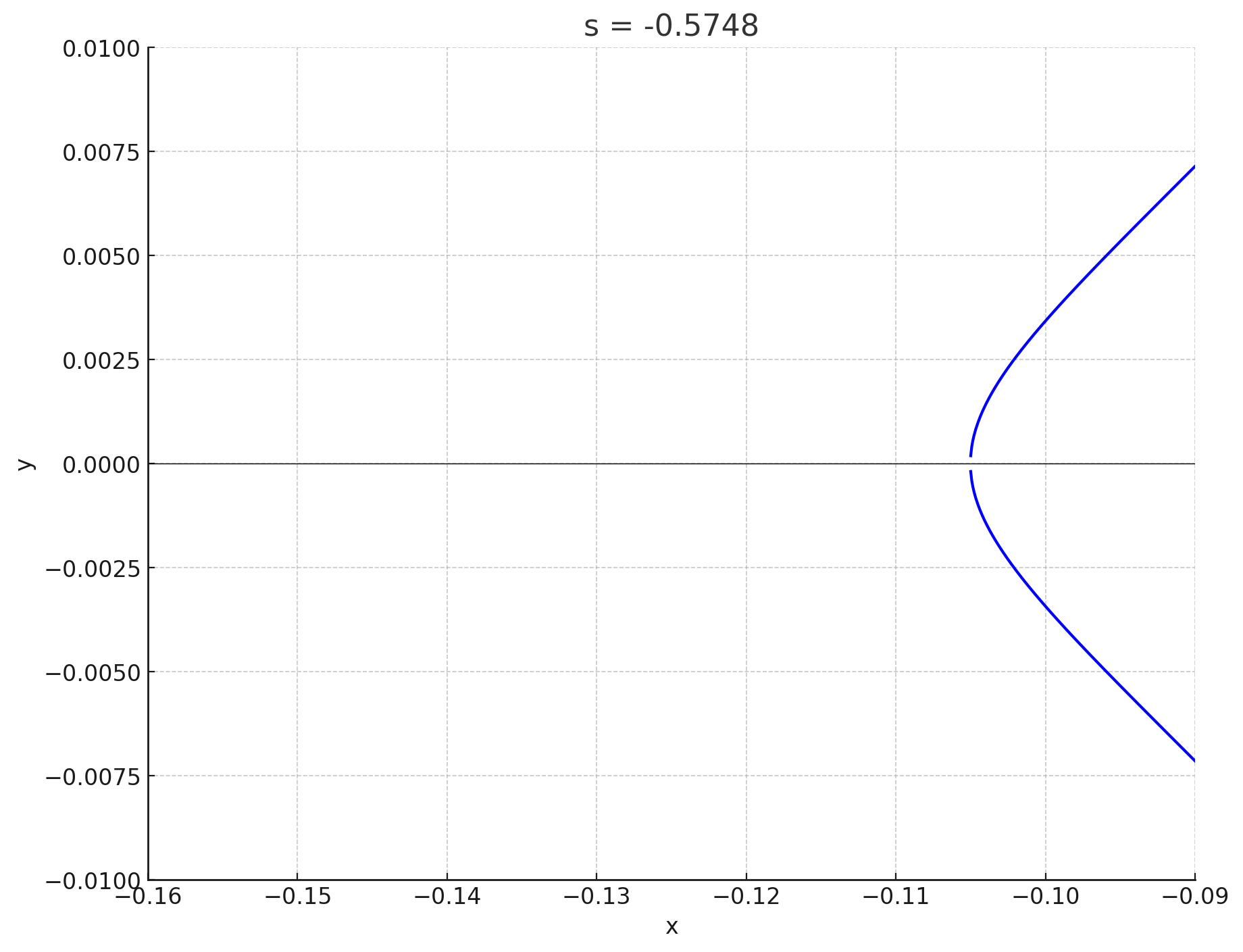s=-0.5748
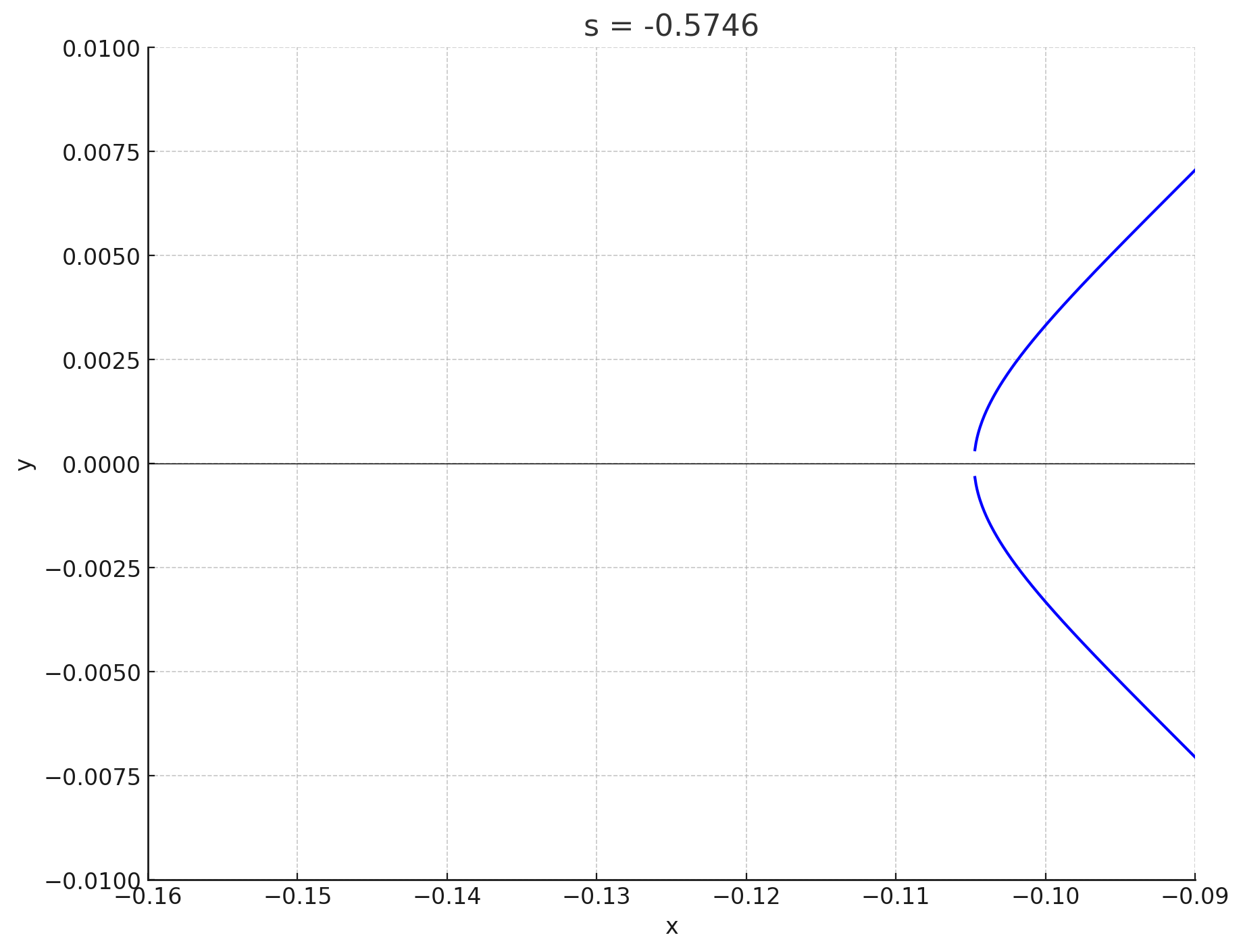s=-0.5746
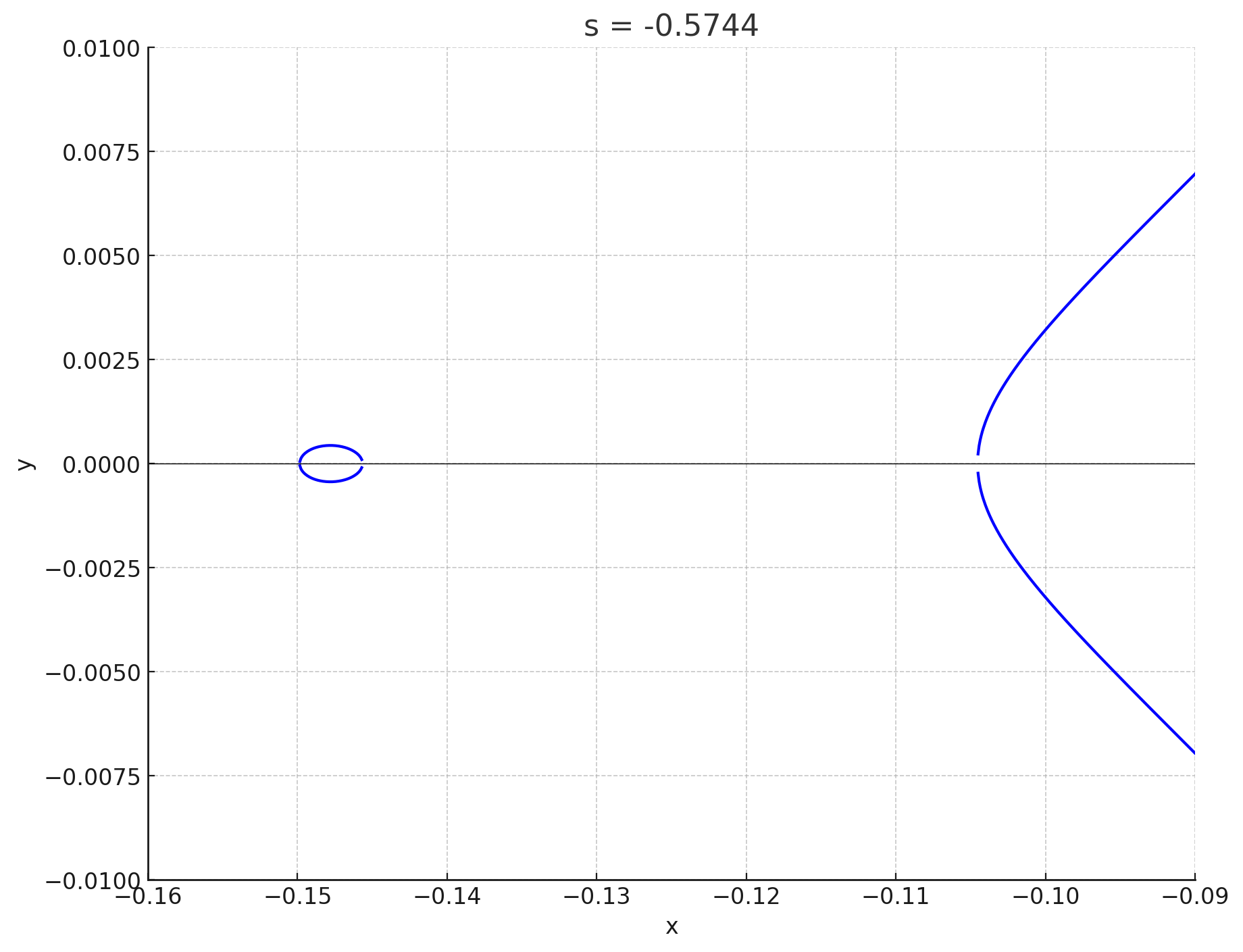s=-0.5744
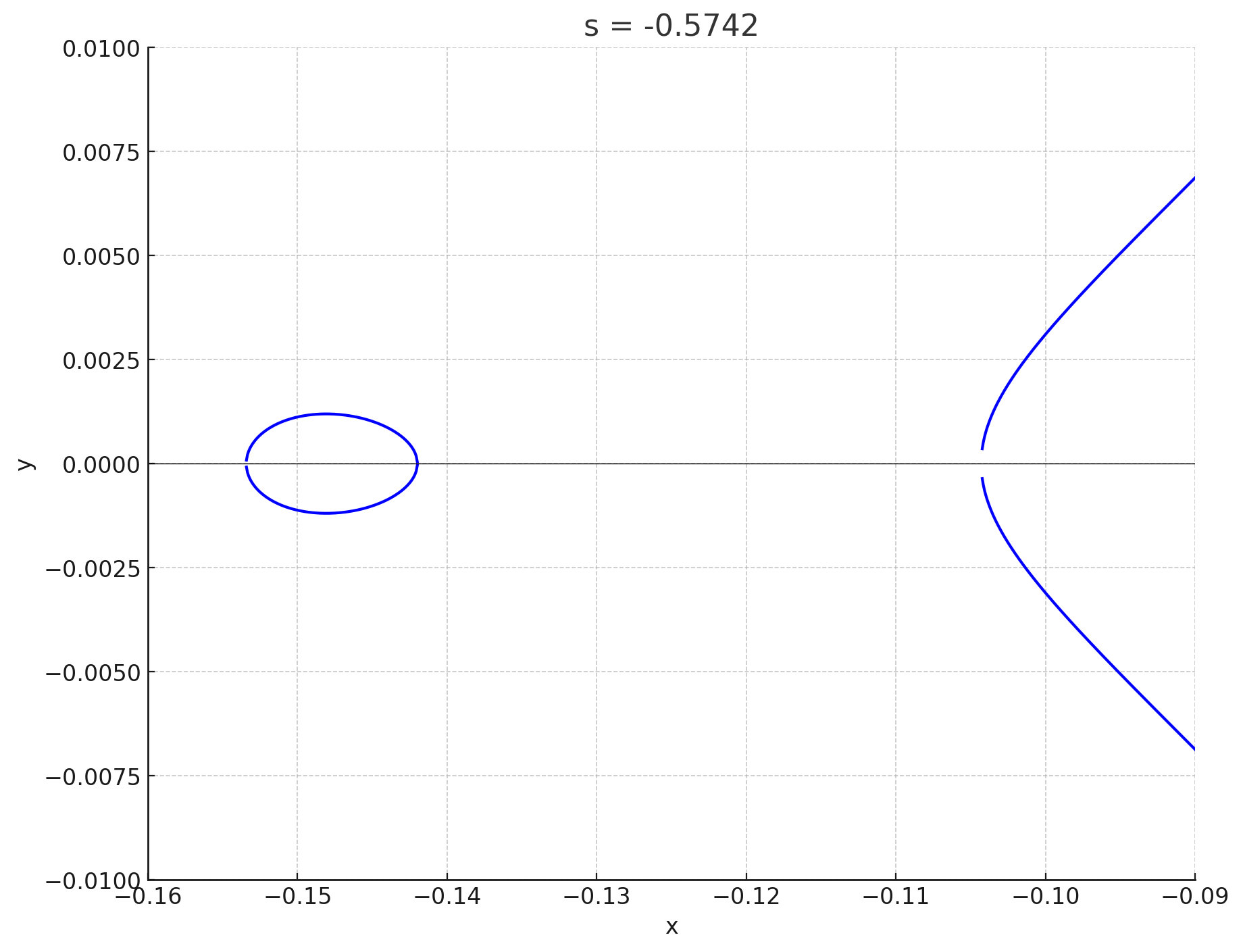s=-0.5742
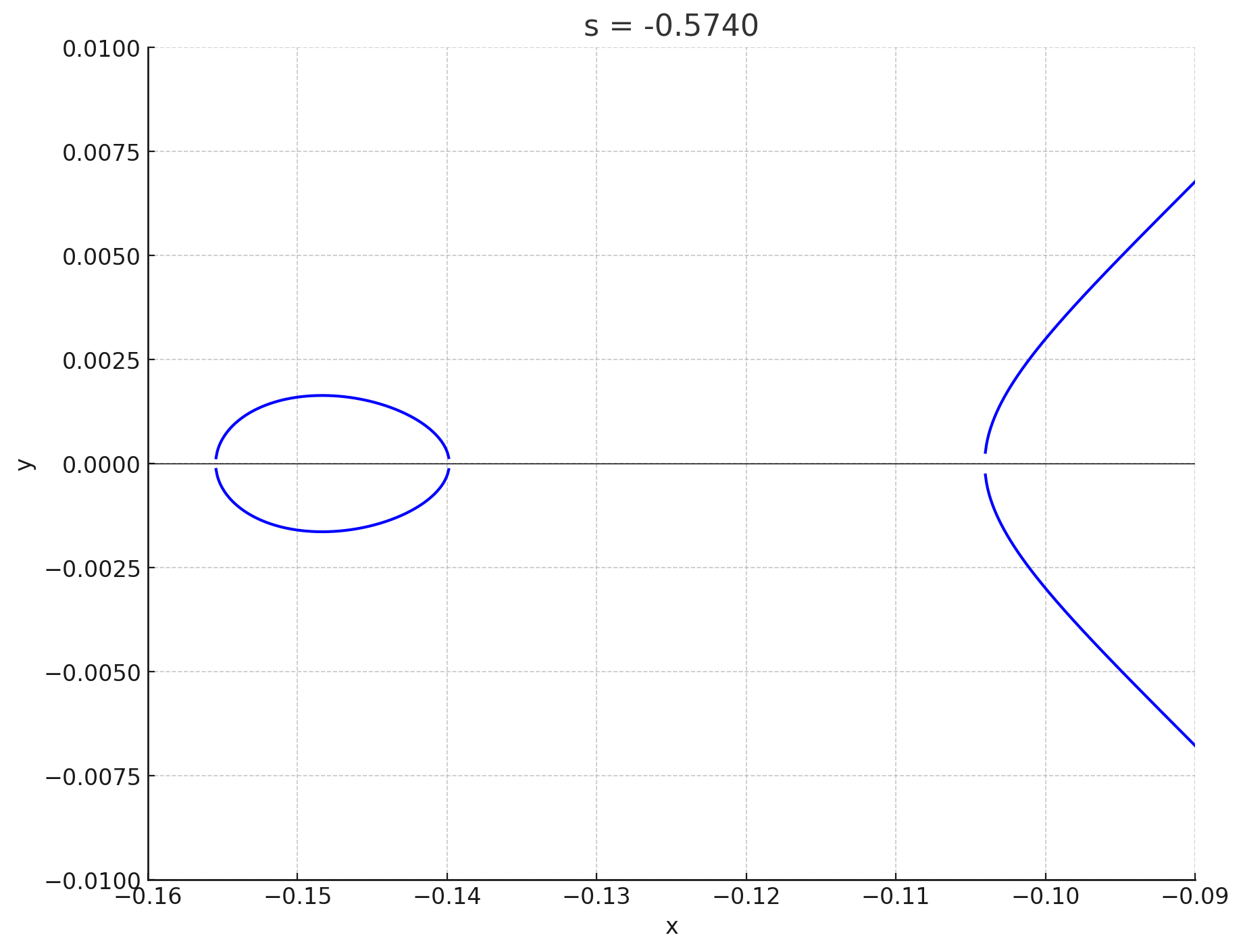s=-0.5740
というわけで，後半の$3$つはなんか輪っかが現れましたね，前半の$3$つにはないのに！勘がいい人はもう気づいていると思うのですが，その境界に何があるかというと，$\psi$を定義するときに除外した点の$1$つである$Q_1$です．(図16の赤いばつ印が$Q_1$です．)

さて，$(s,t)=Q_1$に対しても$b=b(s,t),c=c(s,t)$は問題なく計算できるので，方程式$E(b,c)$を考えることができます．
実際計算すると，$b\approx-0.095563,\quad c\approx -0.103678$なので，方程式$E(b,c)$はおおよそ次の通りです：
$E(b,c):y^2=x^3+0.4001x^2+0.0527x+0.0023$
そのグラフは次の通りになります(曲線および孤立した$1$点からなる)：
$Q_1$に対応する楕円曲線でない代数曲線
これは，楕円曲線にはなりません．$E(b,c)$の右辺の多項式が$x=-0.148$のあたりで重根を持つためです．
($E(b,c)$の左辺を$y^2$から$y$に変更した方程式に対するグラフは次の通り．)
$y$$=x^3+...$としたグラフ
$\psi$を定義する際に$\mathfrak{E}$から$9$個の点を除外しましたが，除外した点に対応する$E(b,c)$は(方程式自体を求めることはできても)右辺が重根を持つため，楕円曲線にはならないのです．それが，除外しなくてはならない理由です．

今$Q_1$について見たように，楕円曲線$E(b,c)$の様相が変化する境界には，除外点があるようです(多分)．

終わりに

いろいろ$\mathfrak{E}$の点に対応するグラフを描いてたら，グラフの変化の境界には除外点があるらしいことがわかって面白かったので記事にしました．ChatGPTに「pythonを使ってグラフを描いて」などと注文すると一瞬でグラフを出してくれるので，いろいろ描いて見ると楽しいですよ．

追記

$\mathfrak{E}$のいくつかの点をサンプルとしてとり，対応する楕円曲線のグラフの概形を調べました．グラフの概形はおおよそ次のように分布しているようです：
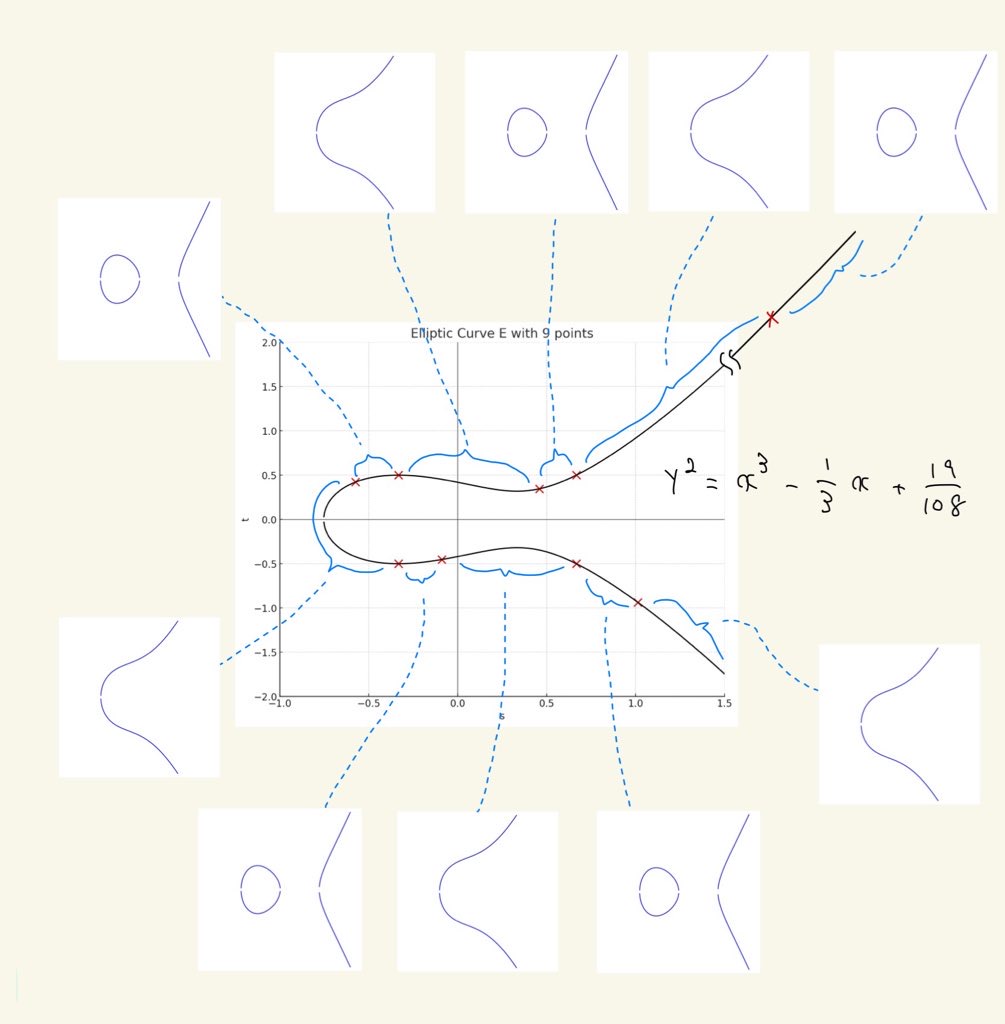グラフの変化
赤いばつ印で表した点が除外点$Q_1,...,Q_9$です．除外点によって楕円曲線$\mathfrak{E}$が$10$の部分に分割され，同じ部分に属する点に対しては同じタイプのグラフが対応します．楕円曲線の$\mathbb{R}$の範囲でのグラフはおおよそ$2$タイプあって，交互にその$2$タイプが現れています．

除外点$Q_1,...,Q_9$に対応する代数曲線も表示したものが次の画像です：
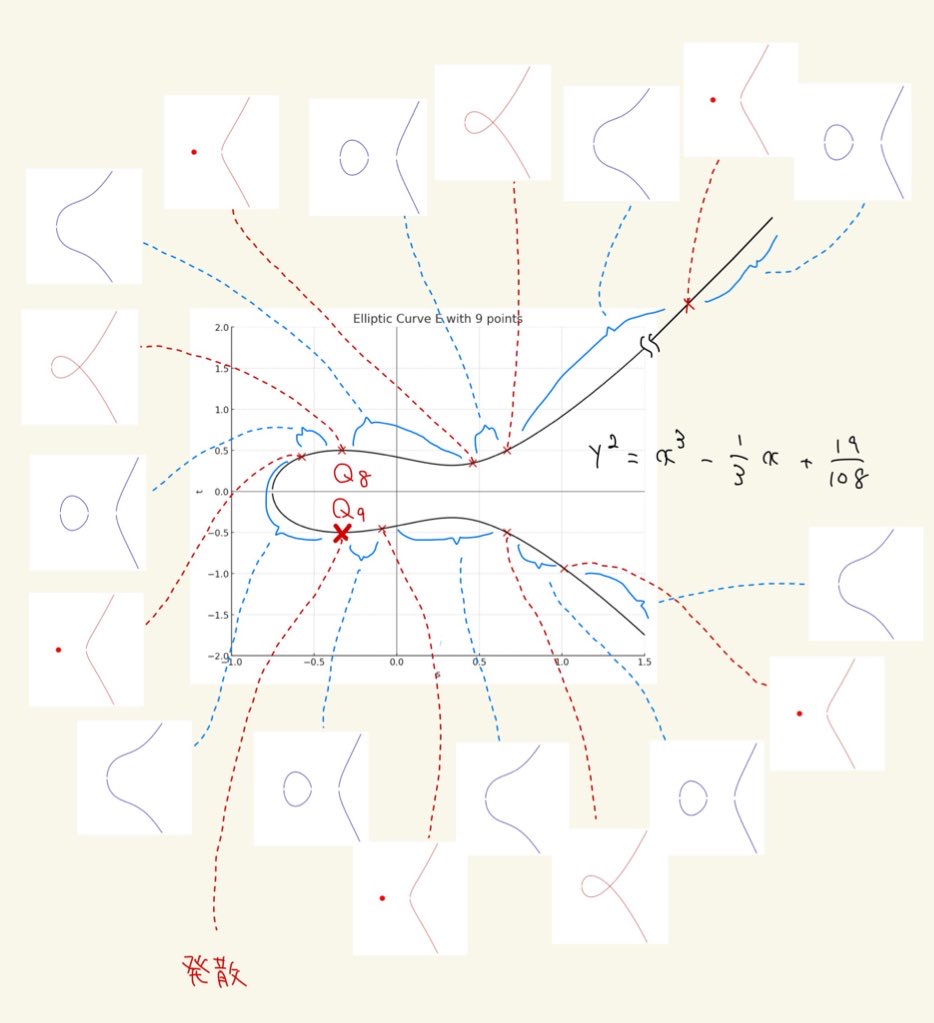除外点込みのグラフの変化
除外点に対応するグラフも$2$タイプあり，これもおおよそ交互に現れています．ただし，除外点$Q_9:=(-\dfrac{1}{3},-\dfrac{1}{2})\in \mathfrak{E}$に対応する$E(b,c)$の係数は発散してしまい，この点に対応する曲線は定義できなさそうです．(この点は除外点の中でもさらに除外される不思議な点です．)

係数が発散するのは，$b(s,t),c(s,t)$の定義式の分母に$s+\dfrac{1}{3}$があるためです．

もう$1$つの除外点$Q_8:=(-\dfrac{1}{3},\dfrac{1}{2})\in\mathfrak{E}$についても$s$座標の値が$-\dfrac{1}{3}$であるため$b(s,t),c(s,t)$は直接は計算できませんが，楕円曲線$\mathfrak{E}$に沿って$(s,t)$を$Q_8$に近づけたときの$b(s,t),c(s,t)$の極限はそれぞれ存在し，いずれも$0$に収束するので，対応する$E(b,c)$は$y^2=x^3+\dfrac{1}{4}x^2$となります．(ということにしました．)