OMC175-E の発展形

はじめに

　この記事は、 仮の人 さんが主催する、 Advent Math Calendar 2023 の12月6日の記事となっています。ぜひ、他の方の記事もご覧ください。
　さて、今回は、OMC175-Eの構図の発展形を紹介したいと思います。まず、OMC175-Eとは、私が作った以下の問題のことです。

　この問題の解答は、 こちら で見ることができます。この記事では、この問題の解き方については説明しないので、気になる方はご確認ください。また、今回はOMC175-Eの本質部分を用いますが、この問題の解き方を理解していなくても、この記事の内容を理解することは可能です。

定理の紹介

　まず、OMC175-Eの本質部分を定式化すると、以下のようになります。

　そして、定理1を用いて今回証明する定理は、以下となります。

　式はそれほどきれいではありませんが、$BC$の長さが外心と内心の距離のみを用いて表されているところが面白いと思います。ちなみに、これは私が自力で導出したものですので、参考文献はありません。

証明

　対称性から、$AB \geq AC$としても$AB \leq AC$としても同じです。ここでは、$AB \geq AC$とします。

　いま、$ \angle BO_1C= \angle BI_1C=120 \degree $なので、四角形$BO_1I_1C $は円に内接します。従って、トレミーの定理より、以下が成り立ちます。
　$O_1I_1 \cdot BC+O_1B \cdot I_1C= I_1B \cdot O_1C$
ここで、$BC= \sqrt{3}O_1B= \sqrt{3}O_1C$ ですから、以下が従います。

　$I_1B-I_1C= \sqrt{3}p \qquad \cdots (1)$

次に、$ \angle BI_1C=120 \degree $なので、定理1(OMC175-E)を適用して以下を得ます。

　$ I_2B^2+I_2C^2=3q^2 \qquad \cdots (2)$

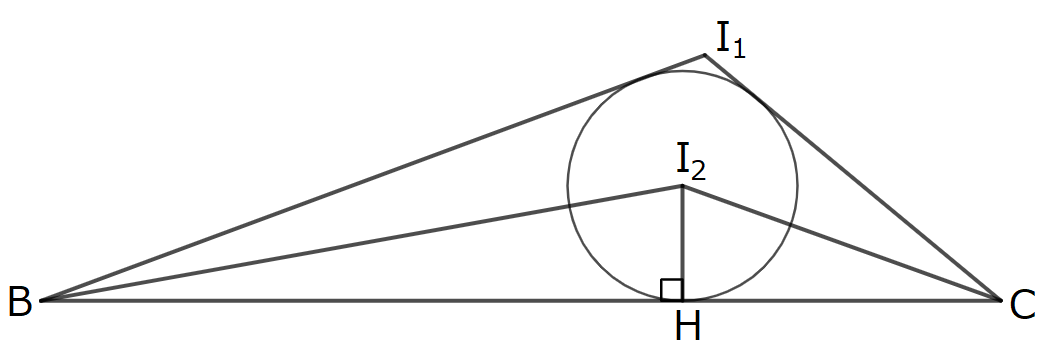
　さて、上図のように、$I_2$から辺$BC$へ降ろした垂線の足を$H$とします。このとき、$BH= \dfrac{BC+I_1B-I_1C}{2}$，$ CH= \dfrac{BC+I_1C-I_1B}{2}$ なので、$(1)$と合わせて、以下が成り立ちます。

　$I_2B^2-I_2C^2=BH^2-CH^2= \bigg(\dfrac{BC+I_1B-I_1C}{2} \bigg)^2-\bigg(\dfrac{BC+I_1C-I_1B}{2} \bigg)^2$

　　　　　　　$= BC (I_1B-I_1C)= \sqrt{3}pBC \qquad \cdots (3)$

また、$ \triangle I_2BC$について、$ \angle BI_2C=150 \degree$なので、余弦定理と$(2)$により以下を得ます。

　$BC^2=I_2B^2+I_2C^2+ \sqrt{3}I_2B \cdot I_2C $

　　　 $= 3q^2 + \sqrt{3}I_2B \cdot I_2C \qquad \cdots (4)$

やったー！未知数三つ($I_2B,I_2C,BC$)に式が三つ($ (2),(3),(4)$)ですね。あとは単なる計算です。
　まずは、$(4)$の$3q^2$を左辺に移行して二乗することで、以下が得られます。

　$BC^4-6q^2BC^2+9q^4= 3I_2B^2 \cdot I_2C^2 \qquad \cdots (5)$

また、$(2)$と$(3)$を用いて、以下を得ます。

　$I_2B^2 \cdot I_2C^2 =\dfrac{ \big(I_2B^2+I_2C^2 \big)^2- \big(I_2B^2-I_2C^2 \big)^2}{4}$

　　　　　　　$= \dfrac{9}{4}q^4- \dfrac{3}{4}p^2BC^2 \qquad \cdots (6)$

$(6)$を$(5)$に代入して整理すると、以下のようになります。

　$BC^4+ \Big(-6q^2+\dfrac{9}{4}p^2 \Big)BC^2+ \dfrac{9}{4}q^4=0$

$BC^2$についての二次方程式です。これを解くと、以下のようになります。

　$BC^2=3q^2- \dfrac{9}{8}p^2 \pm \sqrt{\dfrac{27}{4}q^4-\dfrac{27}{4}p^2q^2+\dfrac{81}{64}p^4}$

いま、$(4)$より、$BC^2 > 3q^2$ですから、プラスマイナスのうちマイナスの方はあり得ません。従って、

　$BC^2=3q^2- \dfrac{9}{8}p^2 + \sqrt{\dfrac{27}{4}q^4-\dfrac{27}{4}p^2q^2+\dfrac{81}{64}p^4}$

となります。　(証明終)

おわりに

　今回は、OMC175-Eを用いて、一つの内角が60°の三角形を考察しました。一番のポイントは、$(3)$の式が$p$を用いてシンプルに表せたことだと思います。$(3)$を思いついたとき、とても嬉しかったです（笑）。
　ちなみに、OMC175-Eは、$\angle BAC= \theta$として一般化可能ですが、それを用いて今回の定理の一般化を導くことは難しそうです（理論上はおそらく可能だと思いますが、複雑すぎます）。また、今回の定理以外にも、OMC175-Eを使って何か導けないかと考えていたのですが、私の力では思いつけませんでした。いろいろと応用できそうな雰囲気はあるんですけどね。
　最後に、次回予告（？）をしておきます。12月10日に、 Mathlogのアドベントカレンダー の記事を投稿します。今回と同様に初等幾何の定理を紹介・証明しますが、今回よりも計算が少なく、個人的に面白い証明だと思っています。ぜひお楽しみに。
　お読みいただきありがとうございました！