文献あり

小学生でもわかる！初等幾何のテクニック/図形と図形を“くっつける”

1156

1章では証明問題が出てきます．また，2，3章のところでは中学数学を使用しています．

初めまして．nmoonです．この記事は AMC2023 (Advent Math Calender) の18日目の記事です．
ぜひ，他の方の記事も読んでってくださいね〜．

0.はじめに

今回の記事では，小学生でも頑張ればわかる(かもしれない)ように主に初等幾何で(特に求値問題で)使われる算数チックなテクニック，“図形をくっつける”について紹介していきたいと思います．(とはいってもやってることはまあまあミケル点)
ぜひ最後まで見ていただければ幸いです．
何気にMathlogで記事を書くのは初めてなので何かご指摘があれば教えてください．

1.図形をくっつける　Part1

とりあえず下の問題を見てみましょう．

$A C = B D$ を満たす四角形 $A C B D$ について， $B C$ の中点を $M$ としたとき， $D$ は線分 $A M$ 上にあった．このとき， $∠ B D M = ∠ C A M$ を示せ．

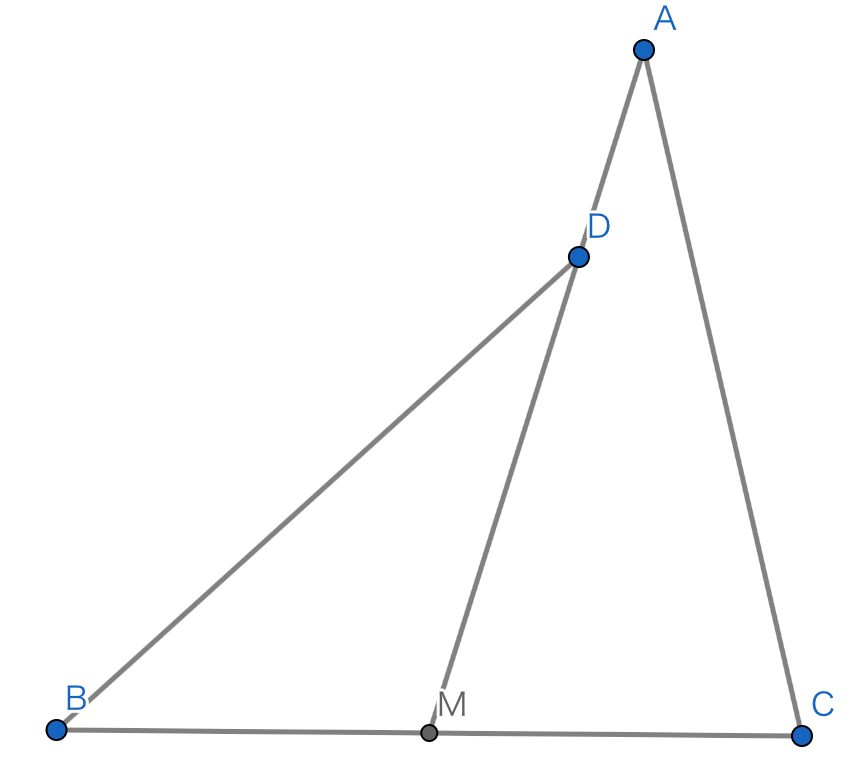例1

~~あれ，求値はどこ？~~
うーん，このまま解くのは難しそうです．方針が全く立ちません．
$A C = B D$ の方の条件は，辺が離れているのでかなり使いづらいですね．こういうときこそ，図形をいろいろ“くっつけて”みましょう.最初は深く考えずに色々くっつけてみることをお勧めします．
今回は例として三角形 $A B M$ と三角計 $C D M$ の2つをを $B M$ と $C M$ でくっつけることを考えてみましょう．
すると，以下の図のようになります．

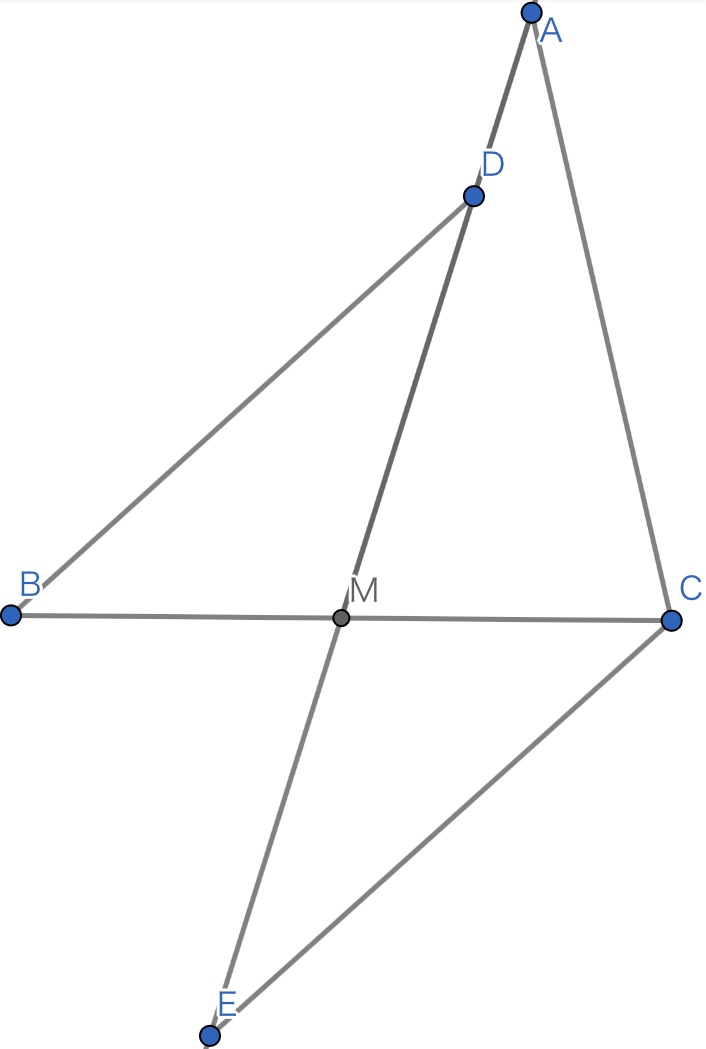三角形をくっつけた

こうすると $C A = C E$ からすぐに結論が得られました！
このように，パッと見たときはどうすればいいか分からなくても，パズルみたいにくっつけていけばわかることがあるのでどうしてもわからない時は試してみるといいかもしれません．

2.図形をくっつける　Part2

せっかくなのでもう一つの場合も見てみましょう．

四角形 $A B C D$ は以下の条件を満たした．
$A B = C D, ∠ B A D = 160^{\circ} ∠ C D A = 80^{\circ}, A D = 4, B C = 6$
このとき，四角形 $A B C D$ の面積を求めてください．

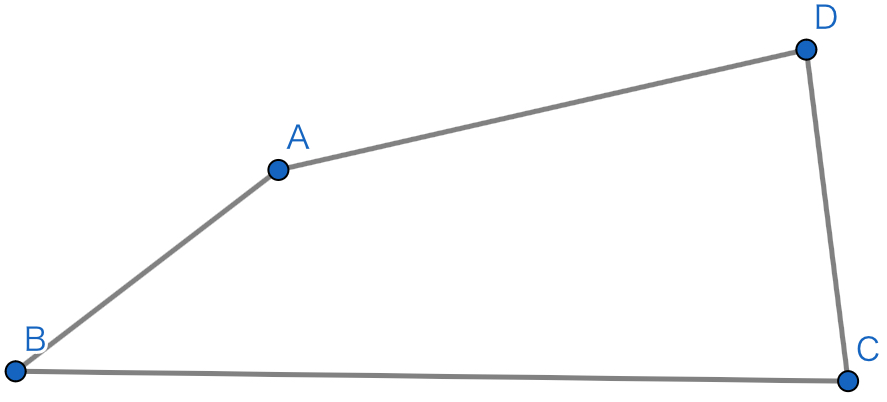例2

角度の条件がウザいですね(コラそこミケル点って言わない)．
こういうときこそ図形をくっつけてみるのが良さそうですね．
しかし，結論を言うと図形2個だけでは足りません！
今回は6個くっつけてみましょう．
すると，以下の図のようになります．

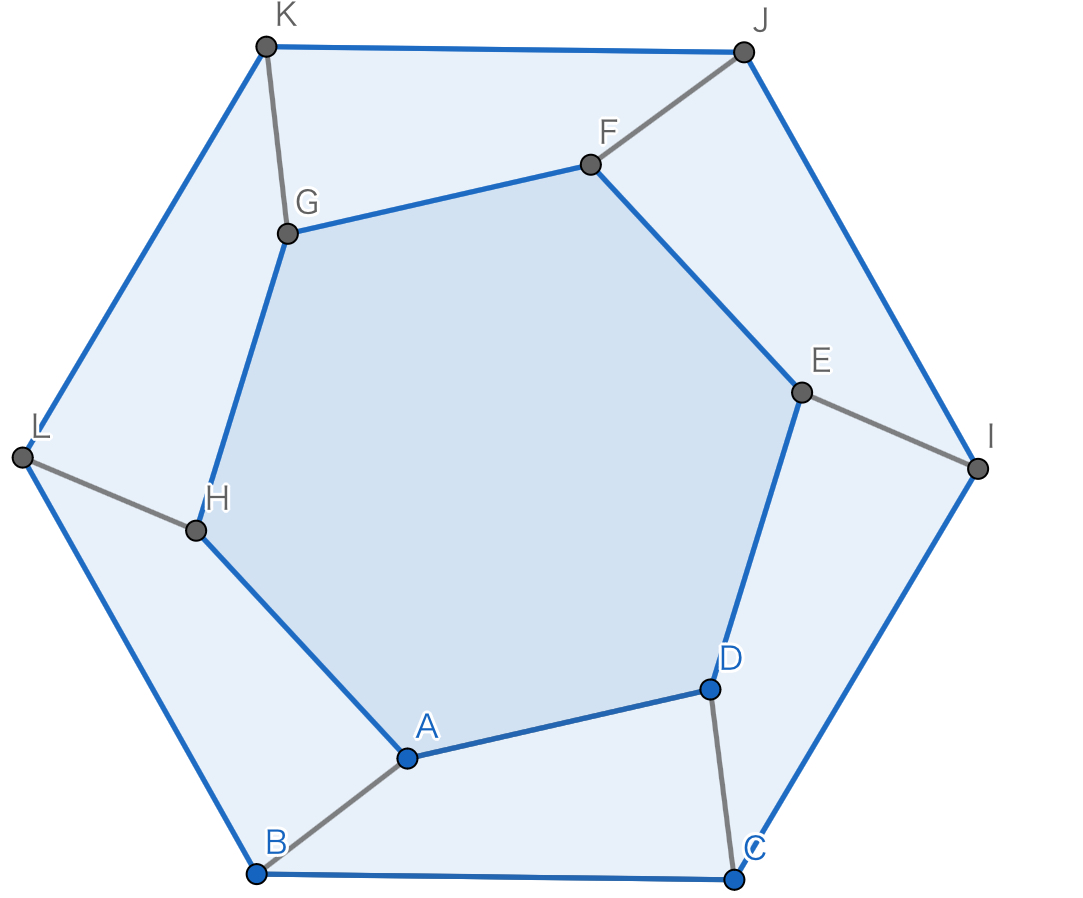たくさんくっつけた

簡単な角度計算から内側と外側にそれぞれ正六角形ができることがわかるので，上の図から

$(6^{2} - 4^{2}) \times \frac{\sqrt{3}}{4} = 5 \sqrt{3}$

と求まりますね．
こんな感じで，同じものを複数個くっつけて綺麗な形を作ることもあるので，できそうであればこちらも試してみてもいいかもしれません．
言いたいことは大体わかってくれたと思うので，あとは練習問題でどんどん演習していってください！

3.演習

OMC172C

凸四角形 $A B C D$ が
$A B = B C = C D, ∠ A B C = {123.45}^{\circ}, ∠ B C D = {116.55}^{\circ}$
を満たすとき， $∠ D A B$ の大きさは度数法で互いに素な正整数 $a, b$ によって $\frac{a}{b}$ 度と表せるので， $a + b$ を解答してください．

解説

こちらから

OMC167E

正三角形 $A B C$ において，その外接円の劣弧 $B C$ 上（端点を除く）に点 $D$ をとり， $D$ に関して $B$ と対称な点を $E$ としたとき， $A D = 7$ および $C E = 4$ が成立しました．このとき，四角形 $A B E C$ の面積の $2$ 乗を求めてください．

解説

こちらから

BMC002G改

一辺が $10$ の正三角形 $A B C$ において，辺 $B C$ の中点を $M$ とする．また，辺 $A B, A C$ 上にそれぞれ点 $P, Q$ をとったとき，以下の条件が成立しました．
$A P = C Q > C P, M P^{2} + M Q^{2} = 72$
このとき， $A P$ の長さは正整数 $a, b$ を用いて $a + \sqrt{b}$ と表されるので， $a + b$ を求めてください．

解説

三角形 $A M Q$ を三角形 $A M P$ の中に入れることでくっつけます．
辺 $A B$ 上に $A Q = A R$ を満たす点 $R$ をとると， $M Q = M R$ がわかる．よって，辺 $A B$ の中点を $N$ とすると，中線定理から $N M^{2} + N P^{2} = 36$ がわかる． $N M = 5$ より， $N P = \sqrt{11}$ なので， $A P = 5 + \sqrt{11}$ で，求める値は $16$ である．

BMC040I

$A B > A D$ である長方形 $A B C D$ を点 $A$ を中心として回転移動させた長方形を $A B^{'} C^{'} D^{'}$ とすると，点 $B^{'}$ は線分 $B D$ (端点ではない) 上にきた． $B D^{'} = 23, B^{'} D = 7$ のとき，長方形 $A B C D$ の面積の二乗を求めてください．

解説

こちらから

OMC099E

凸五角形 $A B C D E$ は次の条件を満たしています．
$∠ A + ∠ B = 270^{\circ}, ∠ D = 90^{\circ}, A B = 2, C D = D E = 7, B C = E A$
このとき， $A B C D E$ の面積としてあり得る最大値と最小値を求め，その和を答えてください．

解説

こちらから

OMC188C

正方形 $A B C D$ において，三角形 $A D C$ の内部の点 $P$ と三角形 $A B C$ の内部の点 $Q$ が $∠ A P Q = ∠ P Q C, A P = 10, P Q = 8, B Q = 9$
を満たすとき，線分 $C Q$ の長さを求めてください．ただし，求める値は正整数 $a, b$ によって $a + \sqrt{b}$ と表されるので， $a + b$ を解凍してください．なお，条件を満たす図は一意に存在します．

解説

こちらから

OMC175E

$∠ B A C = 120^{\circ}$ をみたす三角形 $A B C$ があり，その内心を $I$ ，外心を $O$ とすると，以下が成り立ちました:
$O I = 20, I B = 29.$
このとき，辺 $B C$ の長さの $2$ 乗は，平方因子を持たない正整数 $r$ および正整数 $p, q$ を用いて $p + q \sqrt{r}$ と表されます． $p + q + r$ を解答してください．

解説

こちらから

OMC073F

$∠ A = 100^{\circ}$ なる三角形 $A B C$ において，それぞれ辺 $A B, A C$ 上の点 $D, E$ が $B D = C E$ および $D E = 11$ をみたします．さらに， $B E$ と $C D$ の交点を $F$ とすれば， $B F = 20$ および $∠ B F C = 130^{\circ}$ が成立しました．このとき，五角形 $B F C E D$ の面積は，正整数 $a < b$ によって $\sqrt{a} + \sqrt{b}$ と一意に表せるので， $a + b$ を解答してください．