JMO2024本選体験記

152

この記事にはJMO2024の本選のネタバレが含まれます。
いいですか？

まぁこの記事見る時点でネタバレはご存じでしょうし、この注意は意味をなさないんでしょうけどね。
形だけでも。警告はしたからね

受験前

本質じゃないので読み飛ばしていいです。
前日は早く寝ようと思いながら無為にyoutubeを見てました。0時ごろ就寝。いつもと変わらないです。
当日、四時半起床。 Sigma_Arfさんが五時半らしいので受験者最速でしょう、と思いましたがもうちょっと寝た方がいいと思って寝ました。
解釈によってはおそらくJMO(日本目覚めオリンピック)優勝です。
そのあと十分後ぐらいに再起床、再就寝した後7時頃三度目の起床をしました。
そこから一時間くらいぼーっとしてあったかいおふとんにこもってました。だって寒いし、、、
いつもは(去年のAPMOと春一日目だけなのにいつもとは一体)六本入りのセブンのチョコチップパンを買うんですが、見当たらなかったのでローソンだったかファミマだったかで買いました。いつものより硬かったですね。
~~ローソンとファミマは色が似てるのでどっちがどっちか分かりにくい~~
口の中に味が残ると集中できないかもしれないので特別な味のないただの水を二本買っていきました。

感想

NACGN予想でANCGNだった、4/5ヒットはすごくない？
1,2を一時間、4の誤読で二時間、残り一時間で3を解きつつ4を進めた。
5は知らないです。

問題

$n$ を $2$ 以上の整数とする。 $n$ 個の実数の組 $(a_{1}, a_{2}, \dots, a_{n})$ であって， $a_{1} - 2 a_{2}, a_{2} - 2 a_{3}, \dots, a_{n - 1} - 2 a_{n}, a_{n} - 2 a_{1}$ が $a_{1}, a_{2}, \dots, a_{n}$ の並び替えであるようなものをすべて求めよ．

NACGNの予想だったので初手で外してしまいました。
正直1は何来ても大して変わらないのでいいんですけどね。
とりあえず全部足し合わせると $a_{1} + a_{2} + \dots + a_{n} = 0$ が分かりますね。
天才解があってビビりましたが、ここでは自分の解法を紹介します。

$a_{i - n} = a_{i}$ とする．
$a_{1}, a_{2}, \dots, a_{n}$ の絶対値の最大値を $K$ とし， $| a_{k} | = K$ をみたす $k$ をとる．
$| a_{k - 1} - 2 a_{k} | \leq K$ より， $2 a_{k} - K \leq a_{k - 1} \leq 2 a_{k} + K$ である．
$| a_{k - 1} | \leq K$ であるから，

$a_{k} = K$ のとき　 $K \leq a_{k - 1} \leq 3 K$ より $a_{k - 1} = K$
$a_{k} = - K$ のとき　同様に $a_{k - 1} = - K$
したがって $a_{k} = a_{k - 1}$ ．
これを繰り返せば $a_{k} = a_{k - 1} = a_{k - 2} = \dots = a_{k + 1}$ となるので， $a_{1}, a_{2}, \dots, a_{k}$ は全て等しい値をとる．
総和が $0$ だから， $a_{1} = a_{2} = \dots = a_{n} = 0$

とくにいうことないです。

正の整数に対して定義され正の整数値をとる関数 $f$ であって，任意の正の整数 $m, n$ に対して
$lcm (m, f (m + f (n))) = lcm (f (m), f (m) + n)$
をみたすものをすべて求めよ．

二番がNでした。しかも $lcm$ (最小公倍数)がでてくるというちょっと面白そうな見た目の問題です。
春を目指すならここくらいは最低行きたいところですね。
さて、問題の方に移ります。
$lcm (x, y)$ は $x y$ の約数で、 $x, y$ の倍数です。
また $y$ が $x$ の倍数ならば $lcm (x, y) = y$ です。
これらの $lcm$ の性質をうまく使いながら頑張りましょう。
長いです。もうちょい楽な解法もあるはず。

パート１

与式への $m = x, n = y$ の代入を $P (x, y)$ で表す．
$P (m, m f (m))$ より
$lcm (m, f (m + f (m f (m)))) = lcm (f (m), (m + 1) f (m)) = (m + 1) f (m)$
であるため $(m + 1) f (m)$ は $m$ の倍数である．
よって $f (m) = (m + 1) f (m) - m f (m)$ も $m$ の倍数である．

パート２前半

$P (m, f (m))$ より
$lcm (m, f (m + f (f (m)))) = lcm (f (m), 2 f (m)) = 2 f (m)$
よって $f (m + f (f (m)))$ は $2 f (m)$ の約数．
$f (m + f (f (m)))$ は $m + f (f (m))$ の倍数だから( $∵$ パート１)，
$m + f (f (m))$ は $2 f (m)$ の約数．よって
$2 f (m) \geq m + f (f (m))$
$f (m) - m \geq f (f (m)) - f (m)$
$f$ の $k$ 回合成を $f^{k}$ で表すとすると
$f (m) - m \geq f^{2} (m) - f (m) \geq \dots \geq f^{k + 1} (m) - f^{k} (m)$

パート２後半

$f$ の $k$ 回合成を $f^{k}$ で表す．
数列 $m, f (m), f^{2} (m), \dots$ が狭義単調増加であるとすると $f^{s} (m) \geq f (m)$ をみたす $s$ がとれるのでとる．
$f^{s + 1} (m)$ は $f^{s} (m)$ の倍数で， $f^{s + 1} (m) > f^{s} (m)$ より
$f^{s + 1} (m) \geq 2 f^{s} (m)$
$f^{s + 1} (m) - f^{s} (m) \geq f^{s} (m) > f (m) - m$ となりパート２の前半に矛盾．
またパート１より $m, f (m), f^{2} (m), \dots$ は広義単調増加数列だから， $k$ が十分大きいとき $f^{k + 1} (m) = f^{k} (m)$ となる．

かいてて思った。 $s = 1$ でいいです。すると $f (f (m)) = f (m)$ が示せます。

パート３前編

$P (1, n)$ より
$f (f (n) + 1) = lcm (f (1), n + f (1))$ だから
$f (1) (n + f (1)) = f (1) n + f (1)^{2}$ は $f (f (n) + 1)$ の倍数，よって $f (n) + 1$ の倍数．

パート３中編

$a > f (1)^{2}$ をみたす $a$ と， $f^{k + 1} (a) = f^{k} (a)$ となる十分大きな $k$ をとる．
$n = f^{k} (a)$ とすると
$f (1) n + f (1)^{2}$ は $n + 1$ の倍数だから
$f (1)^{2} - f (1) = [f (1) n + f (1)^{2}] - [f (1) (n + 1)]$ も $n + 1$ の倍数．
$0 \leq f (1)^{2} - f (1) < a \leq f^{k} (a) < n + 1$ より $f (1)^{2} - f (1) = 0$
$f (1) = 1$

パート３後編

パート３の前編より， $n + 1$ は $f (n) + 1$ の倍数だから
$n + 1 \geq f (n) + 1$ ．
パート１より $n \leq f (n)$ ．
したがって $f (n) = n$

あとは十分性について言及すればいいです。忘れないでね。
パート２を $s = 1$ でできたら $P (m, m)$ と $P (m, f (m))$ の比較でもうちょっと早く終わる。
でも絶対もっと楽にできる。
ただ変形してっただけでそこまで難易度はないけど、それでも２番にしては難しいと思う。

$x y$ 平面において， $x$ 座標と $y$ 座標が $1$ 以上 $2000$ 以下の整数である点をいい点とよぶ．
また，以下の条件をすべてみたす４点 $A (x_{1}, y_{1}), B (x_{2}, y_{2}), C (x_{3}, y_{3}), D (x_{4}, y_{4})$ について，折れ線 $A B C D$ をZ型折れ線とよぶ．

$A, B, C, D$ はすべていい点である．
$x_{1} < x_{2}, y_{1} = y_{2}$
$x_{2} > x_{3}, y_{2} - x_{2} = y_{3} - x_{3}$
$x_{3} < x_{4}, y_{3} = y_{4}$

　
$n$ 個のZ型折れ線 $Z_{1}, Z_{2}, \dots, Z_{n}$ が以下の条件を満たすとき，正の整数 $n$ としてありうる最小の値を求めよ．
　
どのいい点 $P$ についても， $1$ 以上 $n$ 以下の整数 $i$ が存在して， $P$ が $Z_{i}$ 上にある．

~~実はいい点じゃなくて良い点なんですけど、まぁいいでしょ~~
問題文が長いのでまずは感覚的に理解することが大事です。
線分 $A B, C D$ は $x$ 軸に平行で，線分 $B C$ は $x = y$ に平行。
で $A, B, C, D$ はそれぞれ左上、右上、左下、右下にある感じ。
Zの横棒がいくらでも伸びる感じですね。
おかわりいただけただろうか、、、

プロローグ

いい点のうち $x$ 座標が $1$ か $2000$ であるような点を最高の点とする．以下の補題を示す．

Z型折れ線に含まれる最高の点は

Z型折れ線が折れ線A(2000,1)B(2000,2000)C(1,1)D(2000,1)と一致するとき四つ
そうでないとき三つ

Z型折れ線が最高の点を含むとき最高の点としてあり得る点は端か角だけ。ってとこからできます。~~書くのがめんどくさい~~

プロロローグ

最高の点は全部で4000個あるので，
$3 (n - 1) + 4 \geq 4000$
$n \geq 1333$

プロロロローグ

$n = 1333$ の構成は可能なので、 $n$ の最小値は $1333$
こんな感じ(これはいい点が!FORMULA[133][35006972][0]個のとき) こんな感じ(これはいい点が $8^{2}$ 個のとき)

構成を思いつくのが結構難しい。
一番最初に思いついた構成が $n = 1999$ 、次が $n = 1500$ です。
四番に時間をかけたの失敗だったかもしれないなぁ。

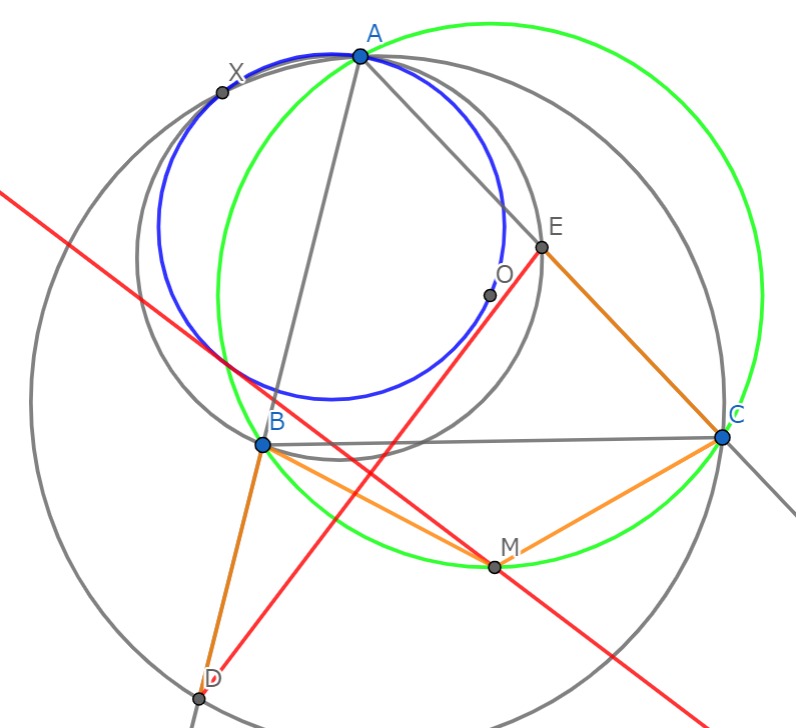
$A B < A C$ をみたす鋭角三角形 $A B C$ があり，その外心を $O$ ，三角形 $A B C$ の外接円の $A$ を含まない方の弧 $B C$ の中点を $M$ とする．
辺 $A B$ の $B$ 側の延長線上の点 $D$ が $B D = B M$ をみたした．また，
辺 $A C$ 上(端点を除く)の点 $E$ が $C E = C M$ をみたした．
三角形 $A B E$ の外接円と三角形 $A C D$ の外接円が $A$ でない点 $X$ で交わってるとき，線分 $D E$ の垂直二等分線は三角形 $A O X$ の外接円に接することを示せ．

点Eは辺AC上です！！！！！！！！！！！！！！
まず図を置いておきます。画像の名前
証明は簡単な部分を省略しながら書いていきますね。

パート１

三角形CEMと三角形BDMは合同である．
そのため四点A,D,E,Mは同一円周上にある．この円の中心をO'とする．
線分DEの垂直二等分線は直線MO'に一致する．
angle-chaseをすると三角形AOO'の外接円は直線MO'に接すること，点O'がAO=O'Oより三角形ABCの外接円周上にあることがわかる．
あとAX//OO'もわかる．

たしかここまで書いた気がする。うーん、、、

おわりに

行ってくれ...！

追記

行った！
88620=24点でしたね。
正直なところ落ちたと思ってて，結果が発表されるまでに3回落ちた夢を見て，1回受かった夢を見ました。 $(逆夢)^{3} (正夢)^{1}$ ってわけか。
3番で時間足りなくて最後構成の図だけ書いてその説明を書けなかったんですが，無事図の意図をくみ取ってもらえたようで思ったより点をもらえたのがよかったですね．
構成を思いついたのがラスト一分なので，皆さんも最後の最後まであきらめないで頑張ってほしいと思います．