2020 ISL C1
以下は僕の解答であり、最善であるとは限りません。逆にいろいろと教えてほしいです。
この記事の目的は個人的なメモでありながら、気になる方々のために出来るだけ思考をわかりやすく説明することです。
よろしくお願いします :)
問題
$n$を正の整数とする。数列$1,2,...,n$の並び替え$a_1, a_2, ..., a_n$で以下を満たすものの個数を求めよ:
$$
a_1 \leq 2a_2 \leq 3a_3 \leq \cdots \leq na_n
$$
考察
まずは小さい$n$で試してみよう:
$1$: $P(1)=1$通り
$2$: $1 \leq 2\cdot 2$ と $2\cdot 1\leq 2$ で$P(2)=2$通り。
$3$:んー ちょっと大変だから表でも作ってみよう。
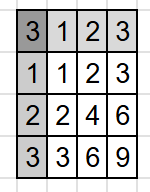 n=3
n=3
縦で何番目に、横で何を選ぶのかを決める。これから使う座標は(縦、横)とする。
例として、 (1,1), (2,3),(3,2) は $a_1 = 1, a_2 = 3, a_3 = 2$を意味する。
つまり、各行と列からちょうど一回ずつ数を選ばないといけない。
(3,1)から始めることはできるか?
できないね。列1にたどり着けない。つまり$a_1 \neq 3$と。。。
逆に数1はどの列に入るんだろう?
うん$a_1 = 1$か$a_2 = 1$が示せるね。
同じように他の数も制限できないかな。。。
もっと大きい$n$で試そう。
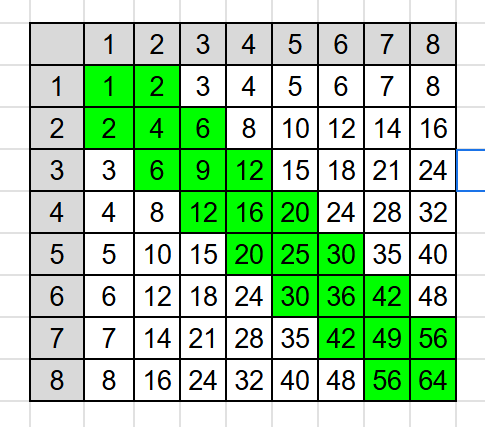 n=8
n=8
通れるマスを探してみたら綺麗な形になった!
これが$n\text{ x }n$のマスにも一般化出来たら解が見つかりそう!
(各行、各列からちょうど一つずつ塗られているマスを選ぶ方法の数)
証明はできそうだし先に解をさがしてみよ。$k\text{ x } k$を考える。
帰納法とかだよね、たぶん。
右下に行$k+1$と列$k+1$のために足してみて、$P(k+1)$を求める。
ん?$k\text{ x } k$に求めた$P(k)$通りは全部マス($k+1, k+1$)に行く。。。つまり($k+1,k+1$)にたどり着くには$P(k)$通りある。
じゃあ($k+1, k$)にたどり着くには?
($k, k+1$)を通らないといけない。じゃあ($k-1, k-1$)か($k-1, k-2$)を通らないといけない。
つまり、$P(k-1)$通りだね。
つまり、$P(k+1) = P(k)+P(k-1)$
フィボナッチじゃーん。
証明の記述は省かせてもらいます。
何を学ぶか
・表に書くとわかりやすい(特にC分野なんだし。。。)
・わかりやすいけど、表だけにとらわれすぎるのも良くない。
実際、この問題は$n$が$n$番目 (他のを決めるのに$P(n-1)$)
か
$n$が$n-1$番目、$n-1$が$n$番目に来ることを示せば (他のを決めるのに$P(n-2)$)
あとは図から離れてみると普通に$P(n)=P(n-1)+P(n-2)$だとわかる。
すると、証明の部分が完全に図なしで簡単にまとめられた。
・似たような問題は意外と帰納法でしめせるから、アイデアが浮かばなければ最初のほうに$P(n+1)$をいじってみるといいかも。