【ネタ記事】ババ抜きの最初って、非効率じゃない?
こんにちは.
${}$
突然ですがみなさん, ババ抜きをしていて次のように思ったことはないでしょうか?
${}$
$$ \huge\text{最初にペアを捨てる時間、つまんな!!!}$$
${}$
本当ですよね. ババ抜きの最初に各自でペアを見つけて捨てる時間はただの作業であり, 何も面白くないです.
そこで今回は, カード編成を変えることで, ゲーム性を保ちつつ最初の時間を効率化できないか?という問題を考えてみます.
${}$
ルールの確認
手番が回る方向は2通りあり得ますが, 「引いた人が引かれる」つまり「BがAから引き, CがBから引く」というように進んでいくこととします.
その他の細かいルールは以下に記します.
ルール (クリックして開く)
・カードはなるべく同数になるように分配する.
・カード整理が終わった後, 誰が最初に引かれるかはランダムに決まるとする.
(現実には整理後枚数が一番多い人から引かれることも多いが, 今回はランダムとした.)
・カードが渡る順は上述のとおり, A→B, B→C, ...という順番とする.
(この逆だと, Jokerが高々1周に1人分しか進まず, つまらないため.)
・Bが残り1枚のときにA→Bとカードを引き, ペア成立しあがったとする. この次はA→Cと引くのではなくC→Dと引くことにする.
(この時同時にAもあがっている可能性があるので, A→Cとすると面倒. Cは引くチャンスを失うが仕方ない.)
${}$
用語と問題の定義
$n$:プレイ人数
$C=(0,1,1,...)$:使うカードの集合. 表記上の都合でJokerは0で表す.
初めにカードを配られてペアを捨てきった後の, ゲームスタート時の枚数を「スタート枚数」とよぶ.
最後の1人になるまでにカードが受け渡された回数を「ターン数」とよぶ.(※周回数ではなく, カードを引いた総回数であることに注意)
${}$
$C$をいろいろと変えてどのようにゲームが変わるのかを調べたいのですが, 「ゲーム性」を評価することはとても難しいです. そこで以下の仮定をおきます.
スタート枚数は, 「ペアが成立して捨てられる快感」という点でババ抜きに必要な要素である.
ターン数は, ゲームを楽しめる時間という点でババ抜きに必要な要素である.
逆に, この2つの値が同じであればババ抜きとして同じものであるとみなすこととする.
※スタート枚数が少なすぎると, ペアができるかドキドキするという醍醐味を失ってしまうので.
${}$
初めの整理の手間を減らすためにはカード総数を減らせば良いので, 問題は次のようにまとめられます.
$C_0=(0,1,1,1,1,...,13,13,13,13)$を通常のトランプの使用カードとする.
カードの集合$C$ であって,
- $C$の要素数は小さい
- 各$n$に対し, $C$と$C_0$のスタート枚数の期待値は近い
- 各$n$に対し, $C$と$C_0$のターン数の期待値は近い
を満たすものを求めよ.
ただし, $C$は$0$を1つ, その他の数字を偶数個ずつ含むものとします.
${}$
通常のババ抜き
さて, まずは$C_0=(0,1,1,1,1,...,13,13,13,13)$の通常ババ抜きの場合に, スタート枚数とターン数の期待値を調べてみましょう.
以下, Pythonで10000回以上シミュレーションをした平均値を掲載します.
| $n$ | スタート枚数 | ターン数 |
|---|---|---|
| 2 | 7.00 | 7.7 |
| 3 | 6.82 | 18.9 |
| 4 | 6.49 | 32.4 |
| 5 | 6.03 | 46.3 |
| 6 | 5.57 | 62.3 |
| 7 | 5.13 | 74.2 |
| 8 | 4.75 | 90.9 |
| 9 | 4.42 | 97.0 |
| 10 | 4.11 | 122.3 |
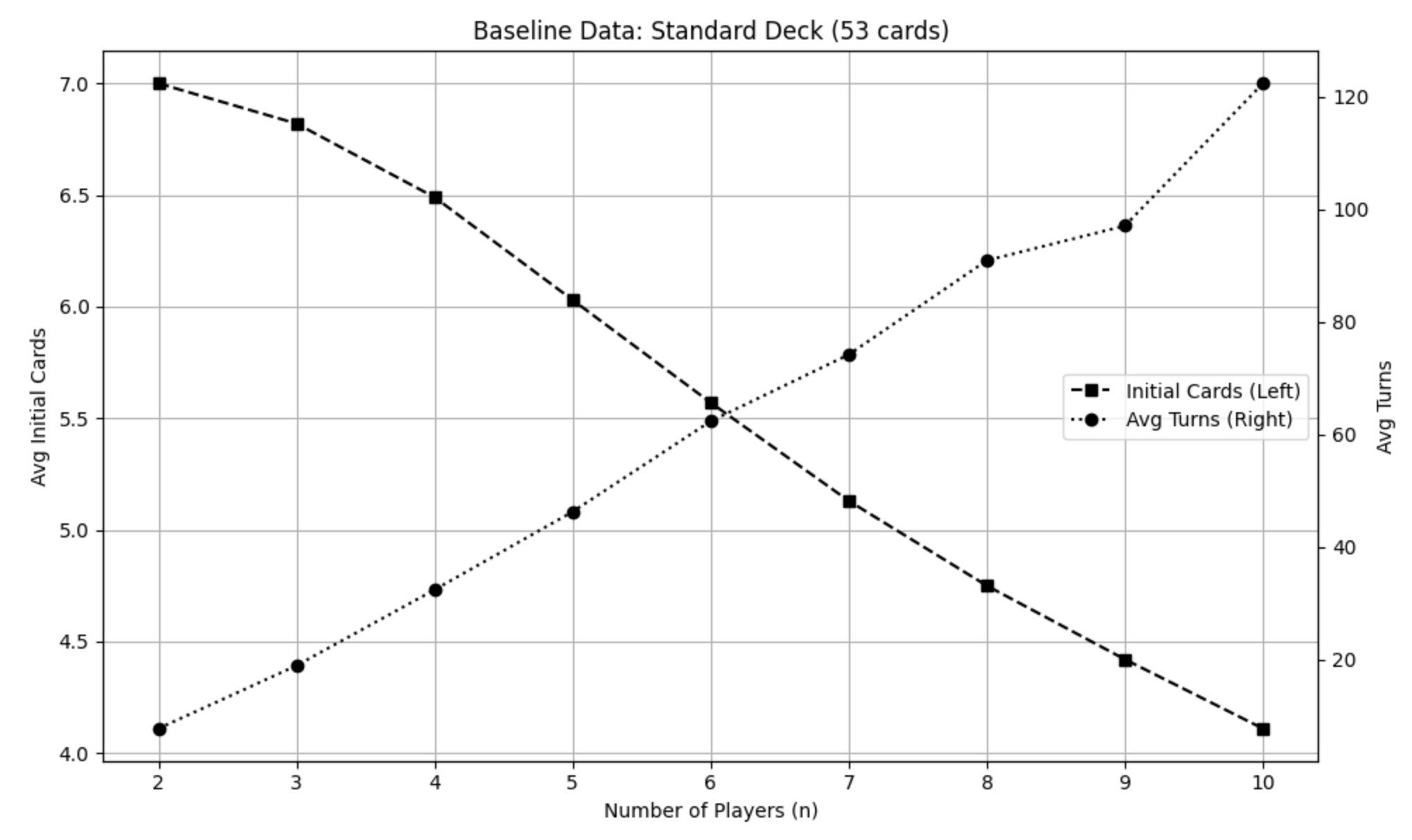 スタート枚数は破線左軸, ターン数は点線右軸
スタート枚数は破線左軸, ターン数は点線右軸
例えば$n=4$のとき, 配られた枚数は平均13.25枚であるのに対しスタート枚数は6.5枚と, 平均3.4ペアも自分で捨てなければいけないことがわかります.
さて, それではこの2曲線をうまく近似するような$C$を探してみましょう.
${}$
戦略
カード総数を減らすために, 何種類かの数字を4枚から2枚にしてみます.
するとペアが成立しにくくなりスタート枚数とターン数は増えるはずです. 一方で全体の枚数が減ったためスタート枚数とターン数も減るはずです.
もしこれが釣り合うとすれば, 全ての数を2枚にした$C=(0,1,1,2,2,...,13,13)$でも通常とほぼ同じ結果になるのではないかと予想してみます. しかし, 調べてみると以下のようになります.
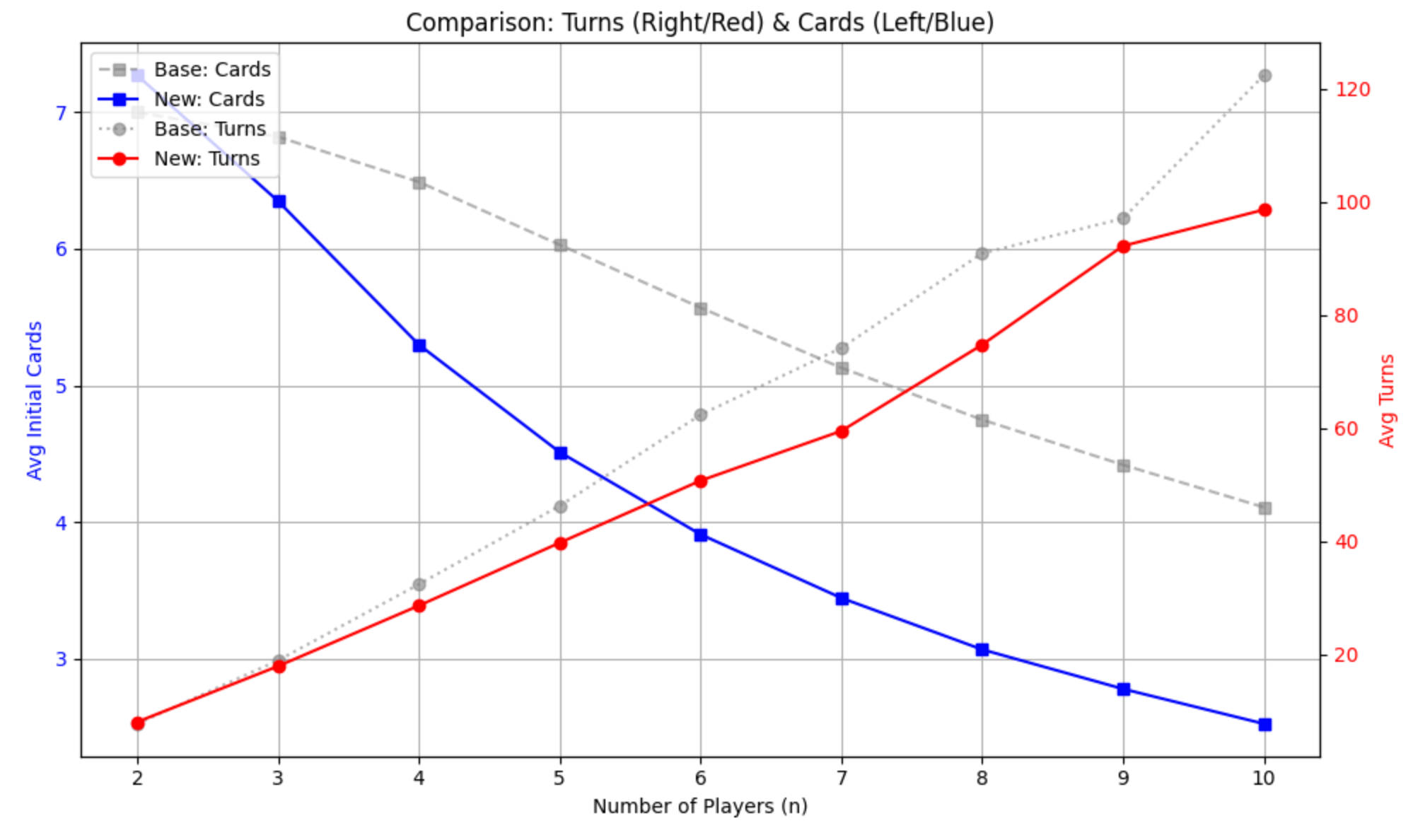 灰色が通常の場合, 青がスタート枚数, 赤がターン数
灰色が通常の場合, 青がスタート枚数, 赤がターン数
$n$が大きいところでかなり差が出てしまいました. (スタート枚数は下端が0でないことには注意)
${}$
そこで, 数字の種類を13よりも増やすことを考えてみましょう. こうすればペアの成立しやすさは変えずに全体の枚数を増やすことができます.
${}$
まずはターン数を合わせにいってみます. $C_k=(0,1,1,2,2,...,k,k)$として, $n=6,7$において横軸を$k$, 縦軸をターン数としたグラフを描いてみます.
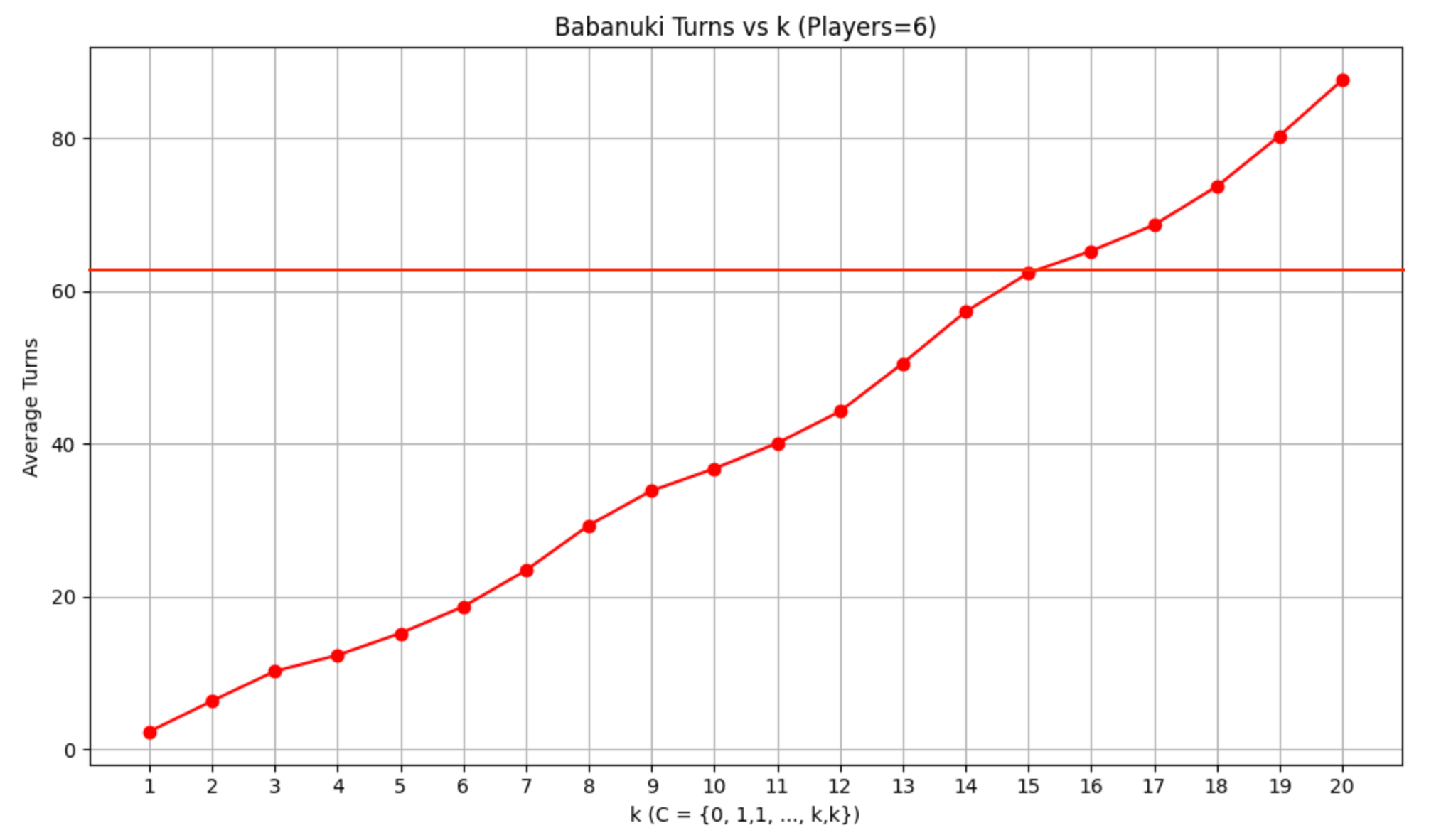 n=6
n=6
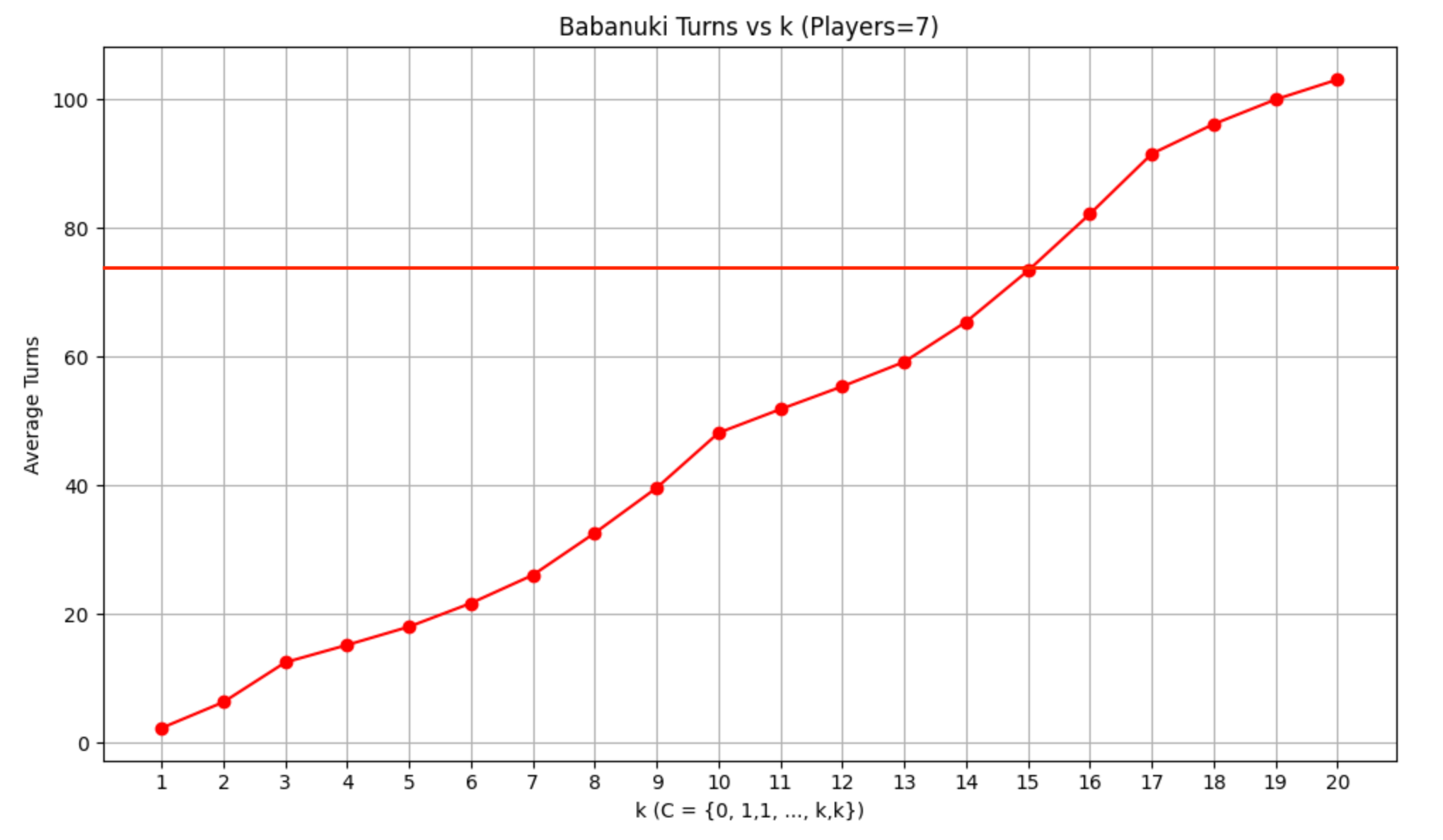 n=7
n=7
ターン数はほぼ$k$と比例していますが, 少し波があります. これはおそらく偶数枚の人数の違いによるものです. (ババ抜きは偶数枚スタートが有利なので)
横線は, 目指すべき「通常ババ抜き」でのターン数です. 見てみるとどちらも$k=15$のときにちょうど一致しそうなことがわかります!
${}$
一方で, スタート枚数を合わせに行こうとすると, 適切な$k$の値は$n$により変わってしまいます. 同様にグラフを書いて調べると, スタート枚数が目標に一致するような$k$の値は以下のようになります.
| $n$ | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| $C_0$でのスタート枚数 | 6.82 | 6.49 | 6.03 | 5.57 | 5.13 |
| 適切な$k$ | 14 | 16 | 18 | 19 | 20 |
| $C_k$でのスタート枚数 | 6.77 | 6.43 | 6.12 | 5.58 | 5.16 |
即ち, ターン数は$k=15$でほぼ完璧に合うが, スタート枚数はそれでは$n=3,4$付近しか合わせられないことになります.
実際, $k=15$で$n$の方を変化させたグラフを描くと以下のようになります.
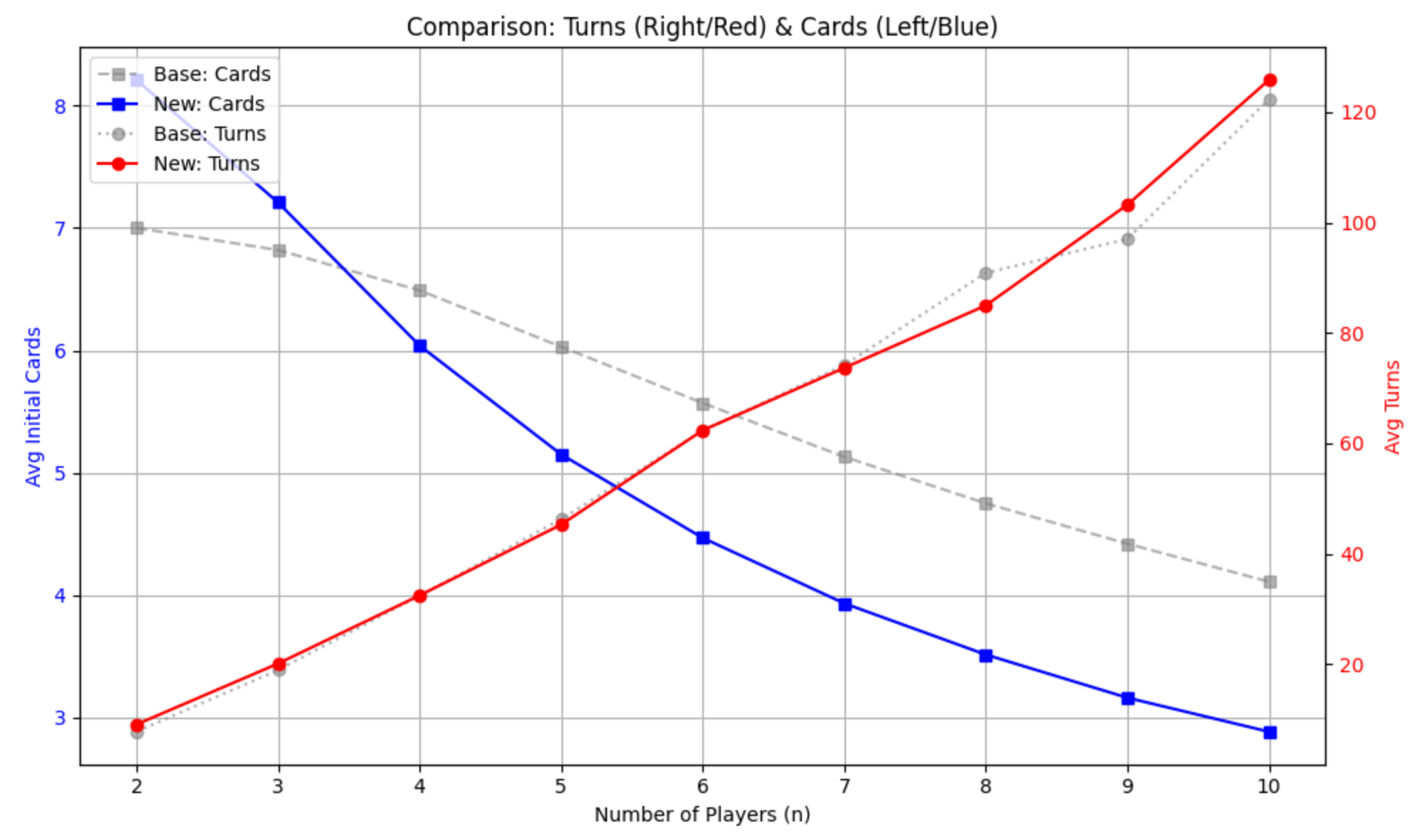 k=15
k=15
赤のターン数は全ての$n$で目標とほぼ一致している一方で, 青のスタート枚数はかなりずれてしまっています.
${}$
最後に$k$を調整して, 赤線も青線も目標からのずれがなるべく小さくなるようにしてみます. 主観ですが$k=17$が最もバランスが取れていると感じました.
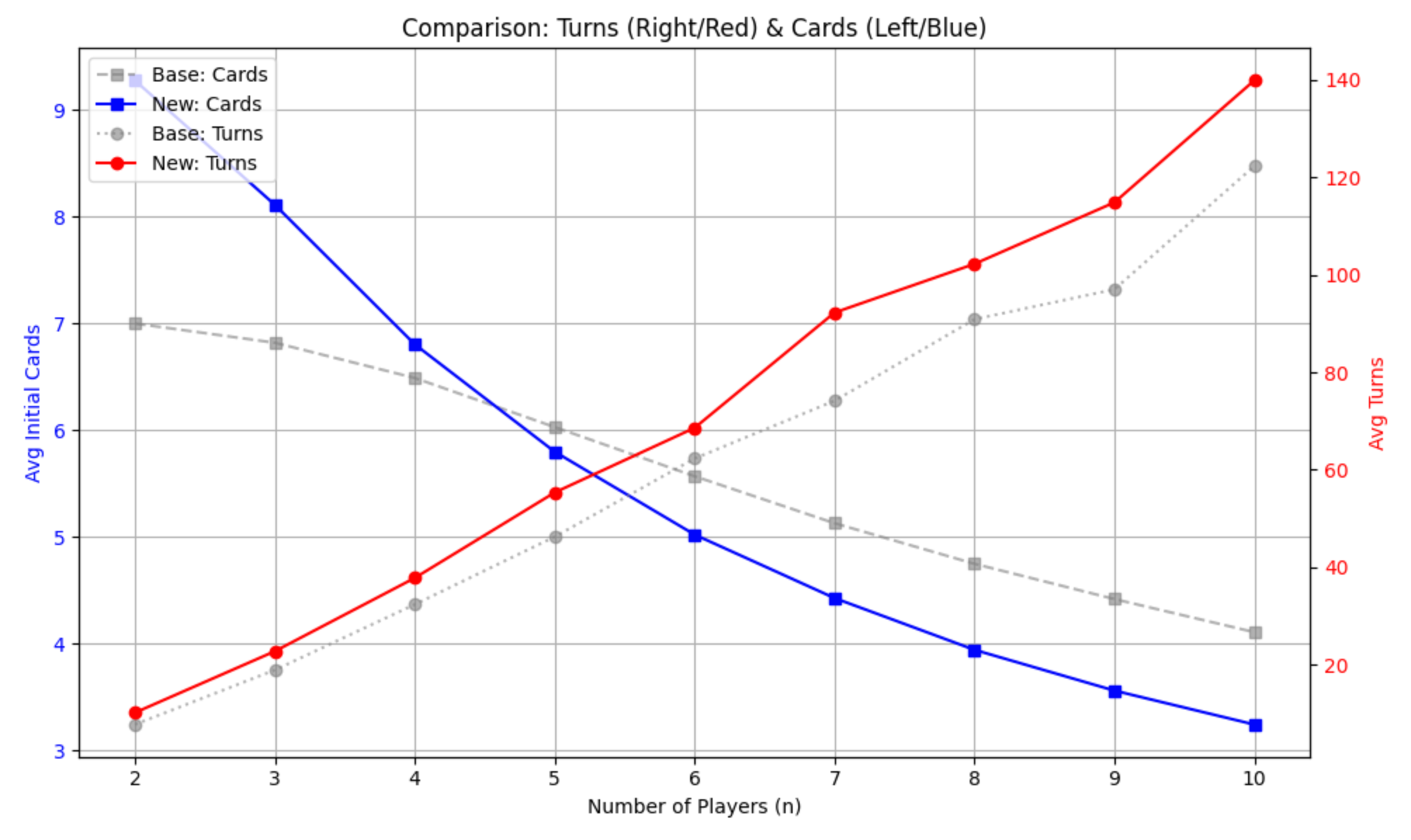 k=17
k=17
ただし, プレイ人数$n$が元々わかっている場合は, 上の表を参照しそれに対応した$k$を選ぶ方が良いです.
${}$
(ちなみに, 全て2枚ずつではなく4枚や6枚用意する数字があった場合も試してみたのですが, こちらはあまりグラフの形に影響しませんでした.)
${}$
結論
ババ抜きは, 通常のトランプ53枚の代わりに
${}$
$$ \huge\text{1〜17が2枚ずつとJokerの35枚}$$
が入ったトランプを使うことで, ゲーム性をあまり変えないまま, 最初に配る時間とペア捨ての時間を短縮することができる.
${}$
もしもプレイ人数が4人と決まっている場合は, 今度は1~16が2枚ずつとJokerが入ったトランプを使うと,
| 通常のトランプ | 特殊トランプ | |
|---|---|---|
| 合計枚数 | 53 | 33 |
| 平均配布枚数 | 13.25 | 8.25 |
| 平均スタート枚数 | 6.49 | 6.43 |
| 平均ターン数 | 32.4 | 34.9 |
のようにゲームの進行をほとんど変えることなく, 「事前捨て枚数」を平均6.76から1.82まで減らし, 準備を効率化することができる.
${}$
ここまで読んでくださった方, ありがとうございました.
${}$
