コラッツ予想の一般項を推測→→→証明してみたいです！！

問題を提起したローター・コラッツの名をとってコラッツ予想と、呼ばれることが多いそうですが、取り組んだ研究者や場所の名を冠して、角谷の問題、米田の予想、ウラムの予想、シラキュース問題などとも呼ばれるそうです。
数学者ポール・エルデシュは「数学はまだこの種の問題に対する用意ができていない」と述べました。また、ジェフリー・ラガリアスは2010年に「非常に難しい問題であり、現代の数学では完全に手が届かない」と述べたそうです。
2019年9月、テレンス・タオはコラッツの問題がほとんどすべての正の整数においてほとんど正しいとするプレプリントを発表しました。

このように、いまだ未解決問題であるコラッツ予想について、考察しました。

ボトムアップ方式で、1から順にコラッツ計算の逆をとって図を作成し、すべての正の整数がコラッツ計算によって最終的に1に到達することを証明する代わりに、1から逆計算をするとすべての正の整数につながることを証明しようと考えました。

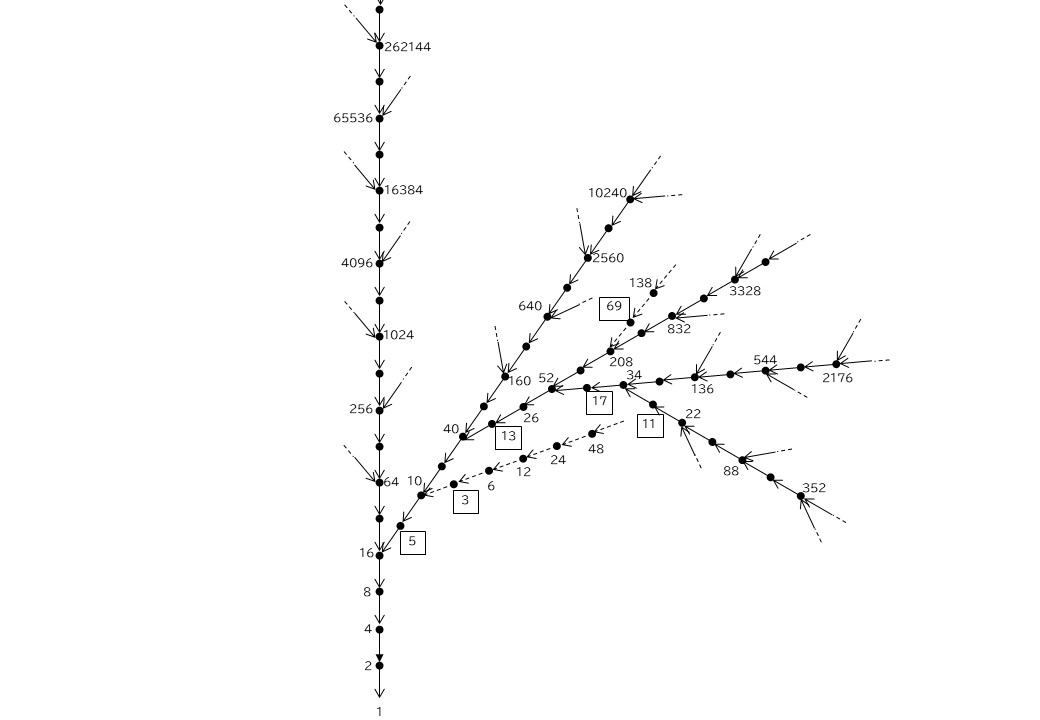コラッツ計算の図

まず、この図において、奇数だけ、偶数だけに着目すると、規則性のある数列であることに気づきました。そして、その数列は、変数を二つ使えば、一般項で示せることにも気づきました。

まず、偶数は、以下のような式で表せます。
$\boldsymbol{ a }$$=$$2^{s}$$\times$$\left( 2t-1 \right)$
2t-1が、枝の最初の奇数で、その枝の先の2倍2倍して続いていく偶数の数列は、tを定数としたsの一般項で示せます。

次に奇数についても考えます。
一本の偶数の枝につながる奇数を抜き出してみましょう。
奇数の並び
すると、やはり規則性を持った数列であり、変数を二つ使えば、一般項で示せそうだと気づきます。
奇数については、枝の根元の奇数が、4で割ったときに1余る奇数か、3余る奇数かで、式が異なってくるため（2で割る回数が偶数回か、奇数回かが変わる）、二つの一般項ができました。
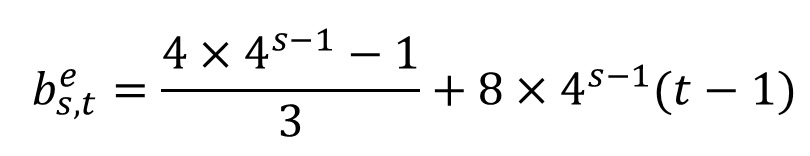奇数の一般項b_e
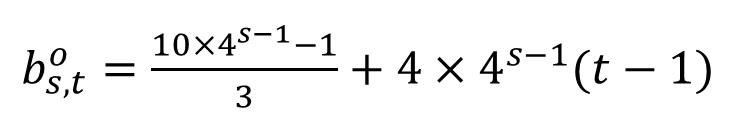奇数の一般項b_o

これらの一般項を、エクセルを用いて、縦横にsとtをとって、かなり大きい数まで計算してみました。
すると、重複ももれもなさそうなのです。
すべての正の整数を表すことができたのか・・・。

ここからは、これらの一般項ですべての正の整数を表せるのかを、証明していくことを考えてみたいと思います。

高校数学Bで学習する、数列の一般項がすべての自然数で成立することの証明・・・数学的帰納法を使って証明しますよね・・・。
でも、このときのすべての自然数って、連続するnであって、数列そのもののことではなかったはず・・・。

なので、まずとりあえずは、s,tがすべての自然数であるときにこれらの一般項が成り立つことを証明しようと考えました。コラッツ計算を漸化関係として、式を変形していくと、このことは、すんなり証明することができそうでした。

でも、数列そのもののがすべての自然数であるときの証明は可能なのでしょうか。これらの3つの一般項で、すべての自然数をもれなく重複もなく示せることを証明しなければなりません。

それには、偶数、奇数、それぞれについて、2ずつ増やしていったときに、これらの一般項が成り立つことを証明すればよいわけですが・・・。

以下のように考えてみました。

まずは、sを定数としたときの数列を考えてみます。
s=1,s=2,s=3・・・とsの値を式に代入して、tだけの式を作っていきます。

偶数の式は
a_(1,t)=4t-2
a_(2,t)=8t-4
a_(3,t)=16t-8
a_(4,t)=32t-16
a_(5,t)=64t-32
a_(6,t)=128t-64

奇数の式は
b_o_(1,t)=4t-1
b_e_(1,t)=8t-7
b_o_(2,t)=16t-3
b_e_(2,t)=32t-27
b_o_(3,t)=64t-11
b_e_(3,t)=128t-107
となります。
（偶数の式も、奇数の式も、4,8,16,32…とtの係数が同じ数をとっていくことがわかります！！）

ここから、偶数（あるいは奇数）を一つずつ（+2）大きくしていくとs,tの値がどうなるのか、見てみました。
縦に偶数（奇数）、横にｓ（奇数の場合はsの値をo,e交互に）をとります。そして表の値はtにします。
偶数の一般項におけるtの値の表（一部）

この表すべてをご覧になりたい方はこちらに載せています。
表2と表5です。
kindle 『あの日の数式』/乃菜佳
～　附録「上山ノート」内に証明の内容を記載しています　～

この表で、ずっと先までみていくと、偶数8個ごとにパターンがあることがわかります。
その一つを見てみましょう！
s=1（4t-2）でtが奇数であるときの偶数の、次の偶数は、必ずs=2（a=8t-4）の偶数をとっています。
tが奇数なので、t=2k+1とおいてみましょう。（このときのaで偶数を表せると仮定します）
これをs=1のときのaの式に代入すると、a=2×(2k-1)となります。
なので、次の偶数は2増えるので、a'=a+2=2×(2k-1)+2です。
これを計算すると、a'=8k-4となります。
s=2のときのaの式はa=8t-4なので、s=1（4t-2）でtが奇数であるときの偶数の、次の偶数は、必ずs=2（a=8t-4）の偶数になることがわかります。
このようにして、8個をひとつのユニットとして、次の偶数がパターンで決まってくることが式の計算で示せます。

なので、数学的帰納法により、最初の9個の偶数でaの式が成立することを示せば、すべての偶数がこの式で網羅できることが証明できそうです。

同じようにして、奇数もまた証明できそうなのです。

奇数は16個をパターンとして、次のtの式が決まってきます。

ゆえに、これらのコラッツ偶数表、コラッツ奇数表には、すべての自然数がもれもなく重複もなく網羅できることが示せそうです。

これらの表は、コラッツ計算過程を示すものなので、すべての自然数でコラッツ計算を施すと1つのパスで1に到達するということが証明できたように思います。

↓こちらにまとめてみています（後半の附録のノート内に証明を記しています）
kindle 『あの日の数式』/乃菜佳