確率の漸化式とペイン(自作問題)
はじめに
地獄へようこそ!はじめまして。ド・ケモノンの法則です。私は数学とケモノを合わせた絶対に需要がないものを作っています。ということで、次の問題を解きましょう。
問題
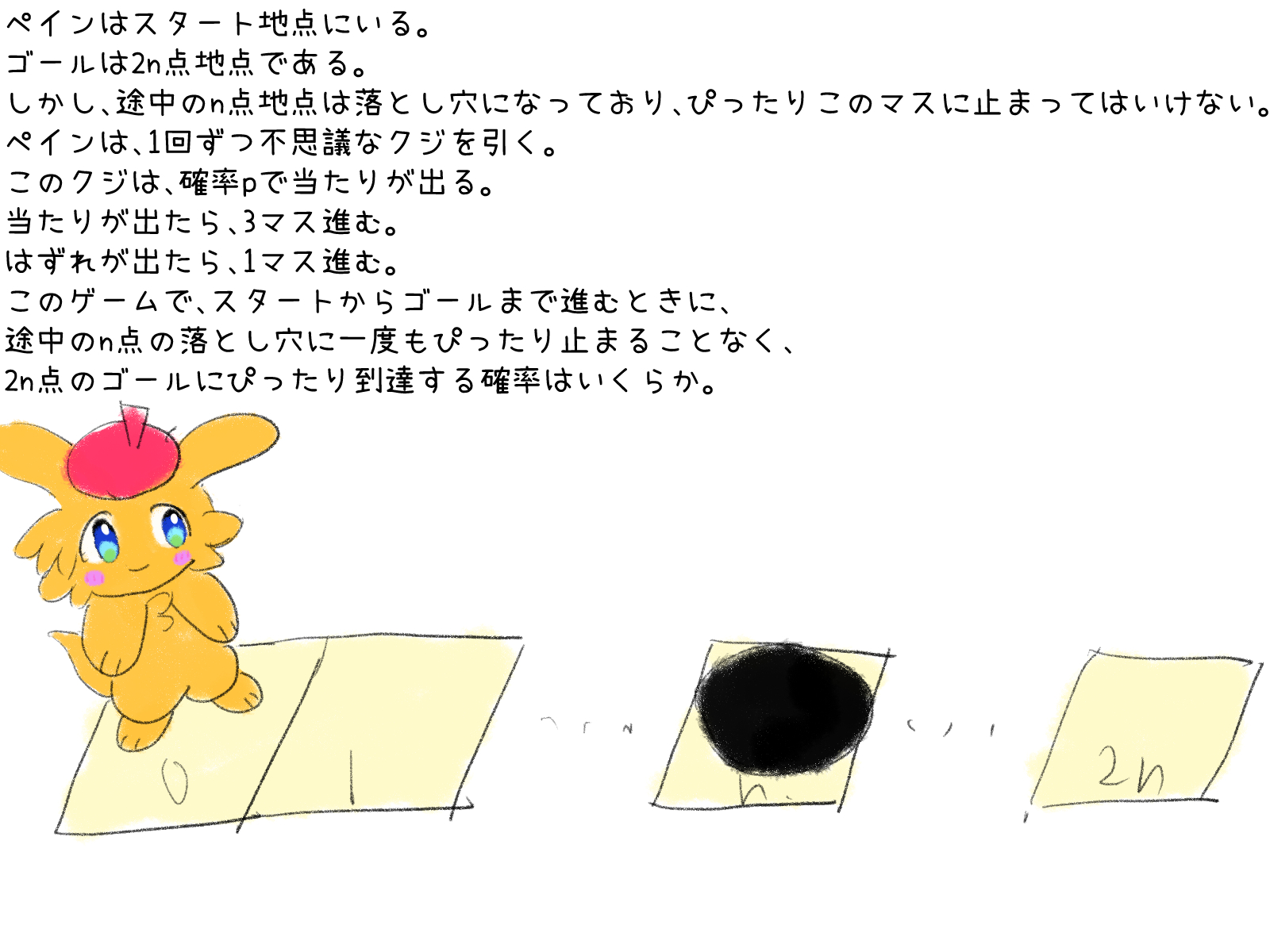 問題
問題
答え
$\frac{p}{(2p+1)^{2}}\left\{ 1+2p^{\frac{n+1}{2}}\cos (n-1)\cos^{-1}(-\frac{\sqrt{p}}{2})+\frac{2p^{\frac{n}{2}}(1-p)}{\sqrt{4-p}}\sin (n-1)\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}^{2}$
解法
くじ引きを繰り返す途中でのr回目で得点の合計がちょうどn+3点になるのは、r-1回目までにn+2点あって、r回目にはずれが出るか、または、r-1回目までにn点あって、r回目に当たりが出るかのどちらかで、それらは互いに排反事象なので、得点の合計が途中でちょうどn点となる確率を$a_{n}$とすると、$a_{0}=1,a_{1}=1-p,a_{2}=(1-p)^{2},a_{n+3}=a_{n+2}(1-p)+pa_{n}$
$a_{n}=A+B(\frac{-p+i\sqrt{p(4-p)}}{2})^{n}+C(\frac{-p-i\sqrt{p(4-p)}}{2})^{n}$と仮定し、実際に漸化式に代入すると成立していることが分かる。よって、
$$
\begin{align}
a_{n}&=A+p^{\frac{n}{2}}B(\frac{-\sqrt{p}+i\sqrt{4-p}}{2})^{n}+p^{\frac{n}{2}}C(\frac{-\sqrt{p}-i\sqrt{4-p}}{2})^{n}\\
&=A+p^{\frac{n}{2}}B\left\{\cos\cos^{-1}(-\frac{\sqrt{p}}{2})+i\sin\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}^{n}+p^{\frac{n}{2}}C\left\{\cos\cos^{-1}(-\frac{\sqrt{p}}{2})-i\sin\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}^{n}\\
\end{align}
$$
ド・モアブルの定理より、
$$
\begin{align}
a_{n}&=A+p^{\frac{n}{2}}B\left\{\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})+i\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}+p^{\frac{n}{2}}C\left\{\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})-i\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}\\
&=A+p^{\frac{n}{2}}B\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})+p^{\frac{n}{2}}Bi\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})+p^{\frac{n}{2}}C\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})-p^{\frac{n}{2}}Ci\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})\\
&=A+p^{\frac{n}{2}}(B+C)\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})+p^{\frac{n}{2}}i(B-C)\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})
\end{align}
$$
D=B+C、E=i(B-C)とすると、
$$
\begin{align}
a_{n}=A+p^{\frac{n}{2}}D\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})+p^{\frac{n}{2}}E\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})
\end{align}
$$
n=0のとき、
$$
\begin{align}
A+D\cos0+E\sin0&=1\\
A+D&=1…①
\end{align}
$$
n=1のとき、
$$
\begin{align}
A+\sqrt{p}D\cos\cos^{-1}(-\frac{\sqrt{p}}{2})+\sqrt{p}E\sin\cos^{-1}(-\frac{\sqrt{p}}{2})&=1-p\\
A-\frac{1}{2}pD+E\sqrt{p(1-\frac{p}{4})}&=1-p\\
A-\frac{1}{2}pD+\frac{1}{2}E\sqrt{p(4-p)}&=1-p…②
\end{align}
$$
n=2のとき、
$$
\begin{align}
A+pD\cos2\cos^{-1}(-\frac{\sqrt{p}}{2})+pE\sin2\cos^{-1}(-\frac{\sqrt{p}}{2})&=(1-p)^{2}\\
A+pD\left\{2\cos^{2}\cos^{-1}(-\frac{\sqrt{p}}{2})-1\right\}+2pE\sin\cos^{-1}(-\frac{\sqrt{p}}{2})\cos\cos^{-1}(-\frac{\sqrt{p}}{2})&=(1-p)^{2}\\
A+pD(\frac{p}{2}-1)-pE\sqrt{p(1-\frac{p}{4})}&=(1-p)^{2}\\
A-\frac{1}{2}pD(2-p)-\frac{1}{2}pE\sqrt{p(4-p)}&=(1-p)^{2}…③
\end{align}
$$
①~③より、$A=\frac{1}{2p+1},D=\frac{2p}{2p+1},E=\frac{2(1-p)}{2p+1}\sqrt{\frac{p}{4-p}}$
よって、$a_{n}=\frac{1}{2p+1}\left\{ 1+2p^{\frac{n}{2}+1}\cos n\cos^{-1}(-\frac{\sqrt{p}}{2})+\frac{2p^{\frac{n+1}{2}}(1-p)}{\sqrt{4-p}}\sin n\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}$
したがって、求める確率は$a_{n-1}^{2}p=\underline{\frac{p}{(2p+1)^{2}}\left\{ 1+2p^{\frac{n+1}{2}}\cos (n-1)\cos^{-1}(-\frac{\sqrt{p}}{2})+\frac{2p^{\frac{n}{2}}(1-p)}{\sqrt{4-p}}\sin (n-1)\cos^{-1}(-\frac{\sqrt{p}}{2})\right\}^{2}}$
コメント
確率を求めるために四項間漸化式を作って特性方程式を解くと1つの実数解と2つの虚数解を得ます。私は虚数を使わないで答えを表記する方が好きなので虚数解を極形式で表記して整理して漸化式の一般項を三角関数を使って表記します。
あとは頑張って計算しましょう。
おわりに
ちなみに、ここで登場したペインくんはばやちゃお様が管理する「魔けモン!」のキャラクターです。かわいいですね。このような感じで今後も需要がない問題を作っていこうと思います。最後まで記事を見てくれてありがとうございました!またどこかで会いましょう!
