幾何演算・幾何関数.１ 幾何演算・幾何関数の定義付け/(正三角形)^2
自己紹介
はじめまして。高校2年生のSosuoと申します。数学が得意というわけではないのですが、とても好きなので、素人なりに頑張ろうと思っています。年相応の数学しか知らないので、私の手法に対してなにか有用なものがあればご教授頂けると幸いです。また、Mathlogへの投稿も初めてなので、拙文極まっていると思っています。勉強しながら活動していこうと思うので、温かい目で見て頂けると嬉しいです。
今回の試みについて
まだ拙い定義となっております。
図形を関数（特に極方程式）として表現（幾何関数）し、直接的な演算を行うこと。ある図形$r_1(\theta)$と別の図形$r_2(\theta)$があるとき、$r_1(\theta)+n [nは任意の数]$や、$r_1(\theta)*｛r_2(\theta)｝^2$などのなにかしらの演算を行い、新たな図形$r'(\theta)$を作成すること。
ある日、図形を関数によって表現することができれば、図形について直接の演算ができるのではないか（$正三角形＋楕円$、$(正三角形)^2$ $etc,,$）と思い、まずは正ｎ角形について関数の形に、特に極方程式によって表現してみたらどうか、と考えました。以降は、正ｎ角形について、極方程式で表す一般的な方法について独自の方法を論じていこうと思います。
正ｎ角形の極方程式化
極方程式を考えていくうえで、まずは簡単のために正ｎ角形や楕円を考える際、図形の中心が極座標の原点に一致しているものとします。
$n=3$の場合について
正三角形は、以下の極方程式によるすべてのｍについての線分の集合として表される。
$r(\theta)=\frac{R}{2cos(\theta-60^\circ-(60^\circ*(2m-1)))} $ $[120^\circ(m-1)\leq\theta\leq120^\circ{m}]$
R:円の半径 $m:0\leq{m}< n$を満たす任意の自然数
半径$R$の円に内接する正三角形を考えます。任意の頂点を基準とし、動径の回転角を$\theta$、動径と正三角形との交点を$点P$とするとき、円の中心$点O$と$点P$との距離を$r(\theta)$とし、以降$r(\theta)$を求めることを目的とします（図1）。
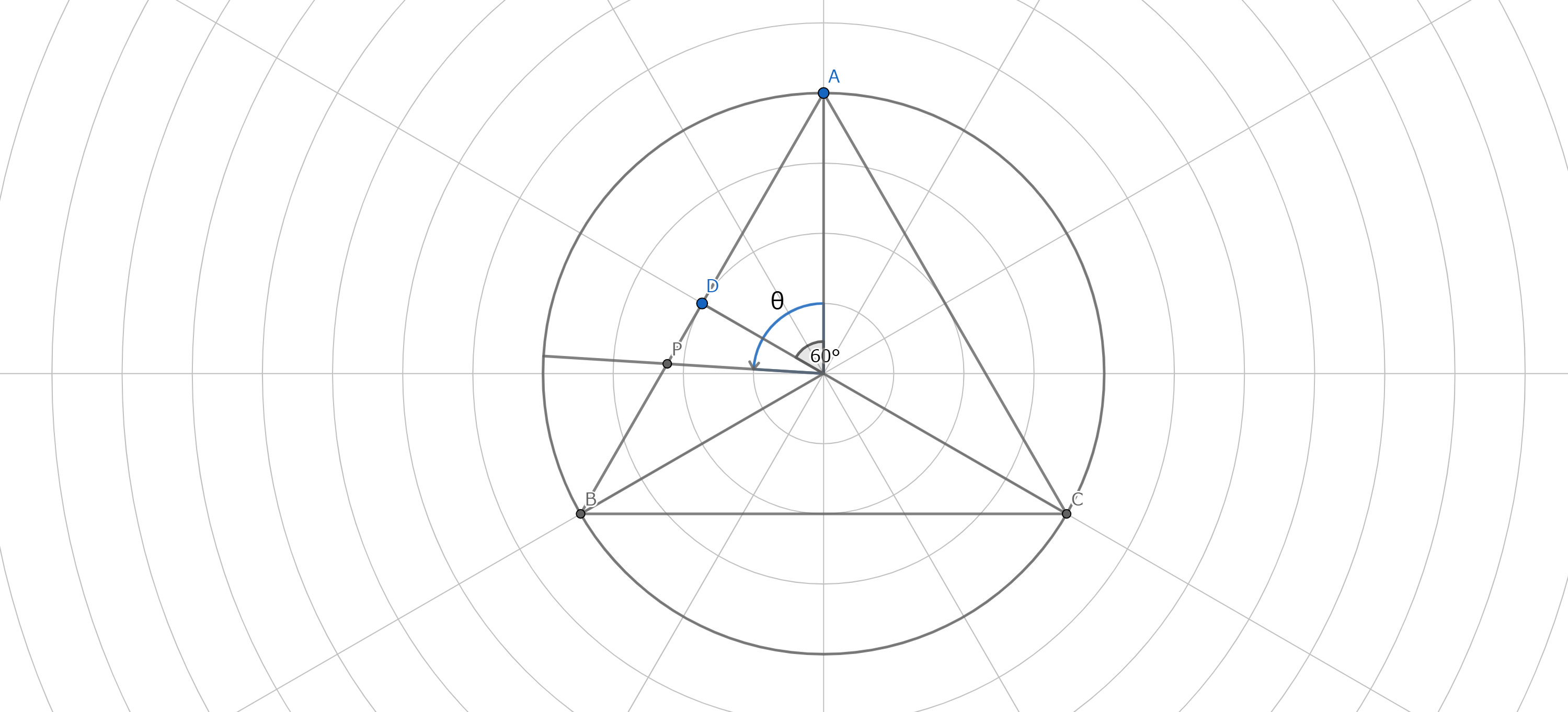
正三角形は$120^\circ$ごとに回転対称なので、$0^\circ\leq\theta\leq120^\circ$までの$r(\theta)$を求め、以降は関数のずらし方と定義域を関連付けることで済みます。
$r(60^\circ)$の時の$点P$を$点D$とすると、$△POD$より$r(\theta)$を求められます。
$0^\circ\leq\theta\leq60^\circ$において、$角POD$は$(60^\circ-\theta)$となるので、
$r(\theta)cos(60^\circ-\theta)=r(60^\circ)=\frac{R}{2}$
$∴ r(\theta)=\frac{r(60^\circ)}{cos(60^\circ-\theta)}=\frac{R}{2cos(60^\circ-\theta)}$
$60^\circ\leq\theta\leq120^\circ$において、$角PODは(\theta-60^\circ)$となるので、
$r(\theta)=\frac{r(60^\circ)}{cos(\theta-60^\circ)}=\frac{R}{2cos(\theta-60^\circ)}$
ここで、$cos(60^\circ-\theta)=cos(\theta-60^\circ)$なので、
$r(\theta)=\frac{R}{2cos(\theta-60^\circ)} [0^\circ\leq\theta\leq120^\circ]…(1)$
ここで、正三角形は$120^\circ$について回転対称なので、$120^\circ\le\theta\leq240^\circ$の場合については、$\theta$について先ほどの結果を$120^\circ$ずらす操作をすればいいです。なので、
$r(\theta)=\frac{R}{2cos(\theta-60^\circ-(2*60°))} [120^\circ\leq\theta\leq240^\circ]…(2)$
同様にして、
$r(\theta)=\frac{R}{2cos(\theta-60^\circ-(4*60^\circ))} [240^\circ\leq\theta\leq360^\circ]…(3
)$
これで正三角形についてすべての$\theta$についての関数がそれぞれできました。以降、定義域と関数を紐づけ、正三角形を一つの関数で表現する試みを行います。
定義域を$120^\circ (m-1)\leq\theta\leq120^\circ{m} (ｍは整数であり、0< m\leq{n})$とするとき、
$r(\theta)=\frac{R}{cos(\theta-60^\circ-(s*60^\circ))}$において、$(s,m)$に対して、$n=3$のとき、(1),(2),(3)より、$(s,m)=(0,1)(2,2)(4,3)$が考えられます。これらから、$s=2(m-1)$が導かれます。よって、
$r(\theta)=\frac{R}{2cos(\theta-60^\circ-(60^\circ*(2m-1)))} [120^\circ(m-1)\leq\theta\leq120^\circ{m}]…(4)$
となり、正三角形についての極方程式が完成しました。以降、ｎについて一般化していきます。
nについての一般化
正ｎ角形は、以下の極方程式によるすべてのｍについての線分の集合として表される。
$r(\theta)=\frac{Rcos\frac{180^\circ}{n}}{cos(\theta-\frac{180^\circ}{n}-(\frac{180^\circ}{n}*2(m-1)))} $ $ [\frac{360^\circ}{n}(m-1)\leq\theta\leq\frac{360^\circ}{n}m]$
$s$と$m$の関係は$n$を変えても引き継がれると考えられます。これより、(4)に登場した具体的な数字$(60と120)$とｎの関係を考えればよいことになります。正ｎ角形について、$角ＰＯＤ$は$\frac{180^\circ}{n}$となります。正ｎ角形についても、先ほどと同様な考え方をして極方程式を構築するため、$n=3$の場合に登場する$60^\circ$は全て$\frac{180^\circ}{n}$として表され、定義域の$120^\circ$は全て$\frac{360^\circ}{n}$と表されます。これを(4)に代入すると、
$r(\theta)=\frac{Rcos\frac{180^\circ}{n}}{cos(\theta-\frac{180^\circ}{n}-(\frac{180^\circ}{n}*2(m-1)))} [\frac{360^\circ}{n}(m-1)\leq\theta\leq\frac{360^\circ}{n}m]…(5)$
と求められます。ｍを１からｎまで動かした時の線分の集合を正ｎ角形とします。
ここで、正ｎ角形の一片の長さは$2Rsin\frac{180^\circ}{n}$です。
desmosにて検証
desmosにて、(5)を用いて、極座標と直交座標で正三角形、正四角形を出力します。
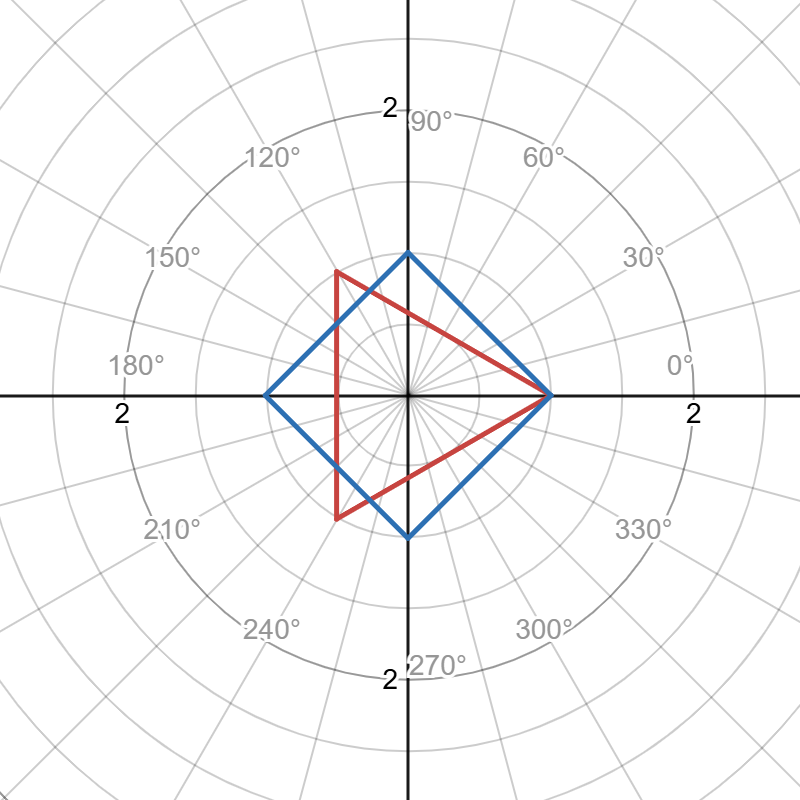赤：正三角形 青：正四角形
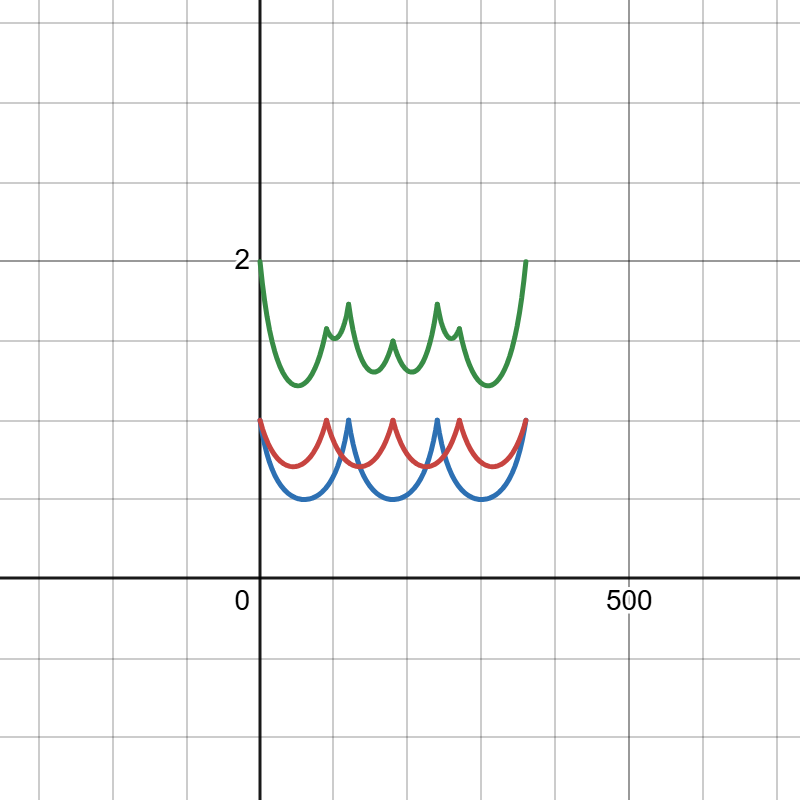
![青：正三角形 赤：正四角形（縦軸が!FORMULA[66][-401913993][0]、横軸は!FORMULA[67][1782773758][0]）](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FQD2uRe8MpDVg60398Jj7.png?alt=media)
青：正三角形 赤：正四角形（縦軸が$r(\theta)$、横軸は$\theta$）
ややこしくて申し訳ないです
正ｎ角形の極方程式を用いた演算
上記の極方程式を用いることで、関数に直に操作を加え、新たな図形を作成することが出来ます。
ex.)$正三角形＋\alpha 、正三角形-正四角形、(正三角形)^2$
主なイメージとしては、すべての$\theta$についての$r_1(\theta)$、$r_2(\theta) $について任意の演算を行った結果をあらたに$r'(\theta)$として作成するイメージです。
ex.)$r_1(1^\circ)+r_2(1^\circ)=r'(1^\circ)、r_1(2^\circ)+r_2(2^\circ)=r'(2^\circ)$
例１ $正n角形＋正n'角形$
先ほど作成した関数を用いて、正ｎ角形と正ｎ’角形について関数で表現し、それぞれを足し合わせます。ここで大切なのは定義域です。例えば正三角形と正四角形を足し合わせる場合、図３より、定義域が切り替わるところが違いますから、そこを考えなければなりません。なので、新たに作られる図形の関数の定義域は、元の関数の定義域の周期ごとに定義しておく必要があります。図３では、
$0^\circ\leq\theta\leq90^\circ , 90^\circ\leq\theta\leq120^\circ,120^\circ\leq\theta\leq180^\circ,180^\circ\leq\theta\leq240^\circ,240^\circ\leq\theta\leq270^\circ,270^\circ\leq\theta\leq360^\circ$
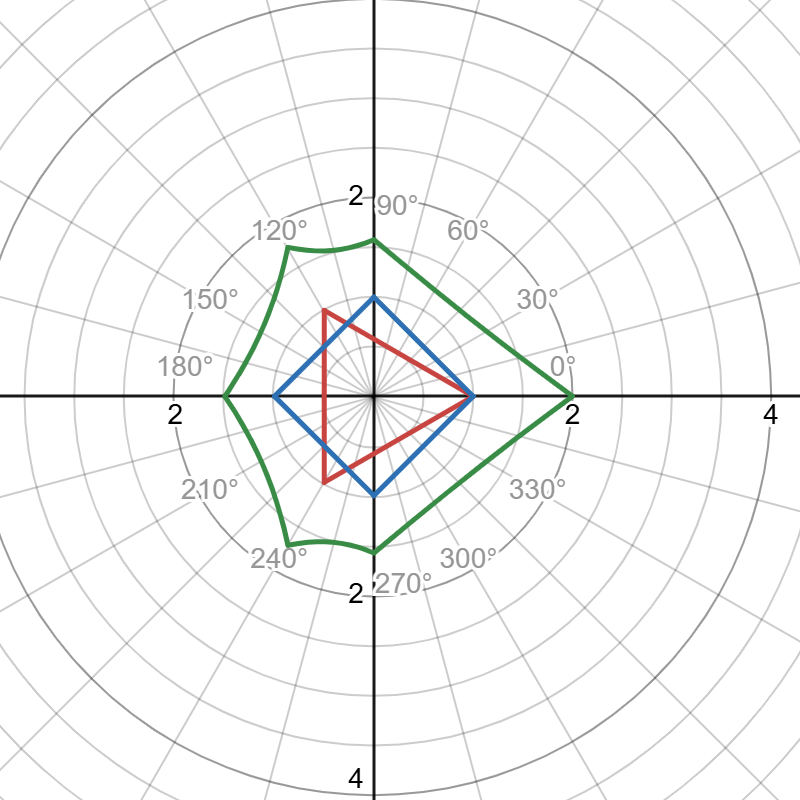
の６つになります。それをもとに関数を作成し、desmosにて描画したものが図４、図5、図6です。
緑：正三角形＋正四角形
正三角形＋正四角形
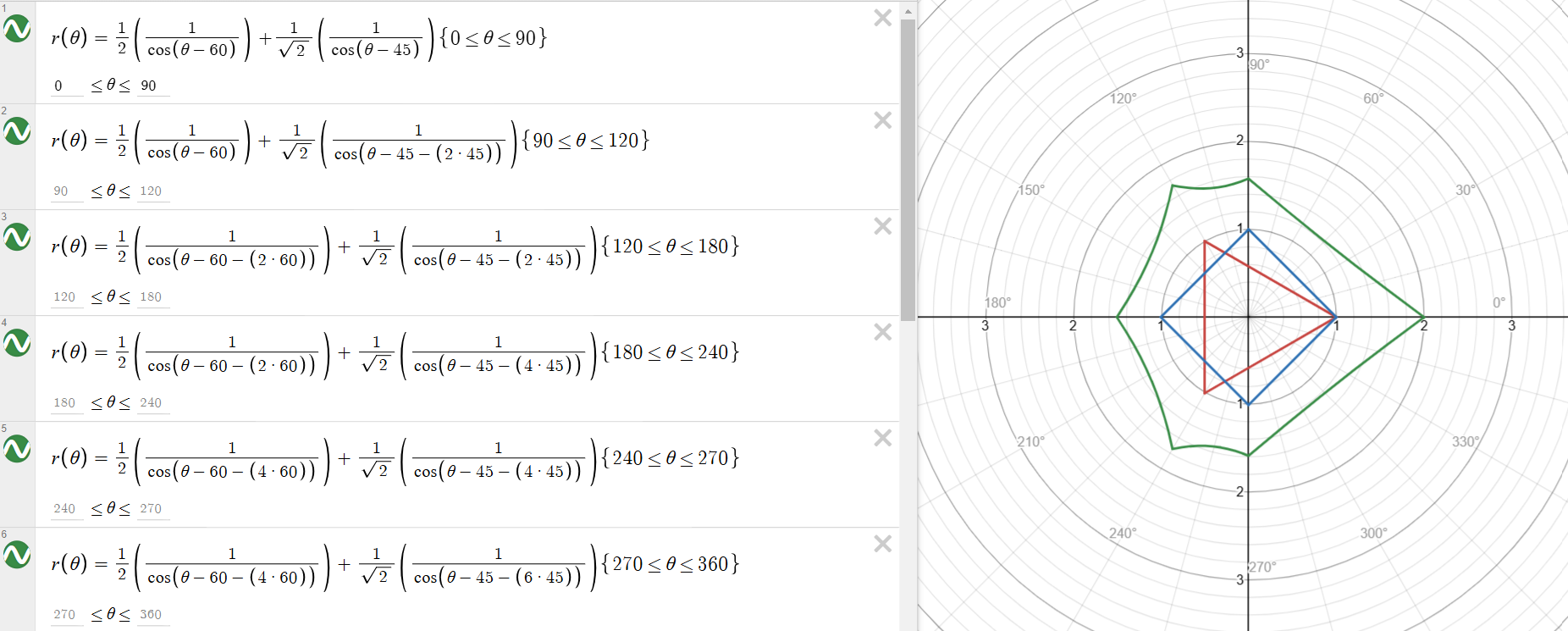極座標 数式
このように、新たな図形を作成することが出来ます。また、今回は原点から頂点までの長さを同じにしていますが、これを変更することも出来ます。
例２ $正ｎ角形*正ｎ’角形$
加法と同様にして、乗法についても定義できます。それをもとに極座標に描画したものが図7です。
![!FORMULA[77][-627754324][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F2VZ4PHZqIyuHkartoC2m.png?alt=media)
$正三角形＊正四角形$
$正三角形^2$は図8です。
![!FORMULA[79][911472982][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FRb8KT0BuDaNMOwKpTisn.png?alt=media)
$正三角形^2$
例３ $\frac{正ｎ角形}{正ｎ’角形}$
これも先ほどと同様にして、定義域を設定することで、定義することが出来ます。極座標に描画したものが図９です。
![!FORMULA[81][-1922230664][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FPmhgSGMKBOiZhUVXBgw0.png?alt=media)
$\frac{正三角形}{正四角形}$
例4 $正ｎ角形+\alpha(自然数)$
これについては、定義域について考えないでいいので楽です。ただ、定義域を決めないと、変なグラフになります。これについてはまた考えてみたいと思います。
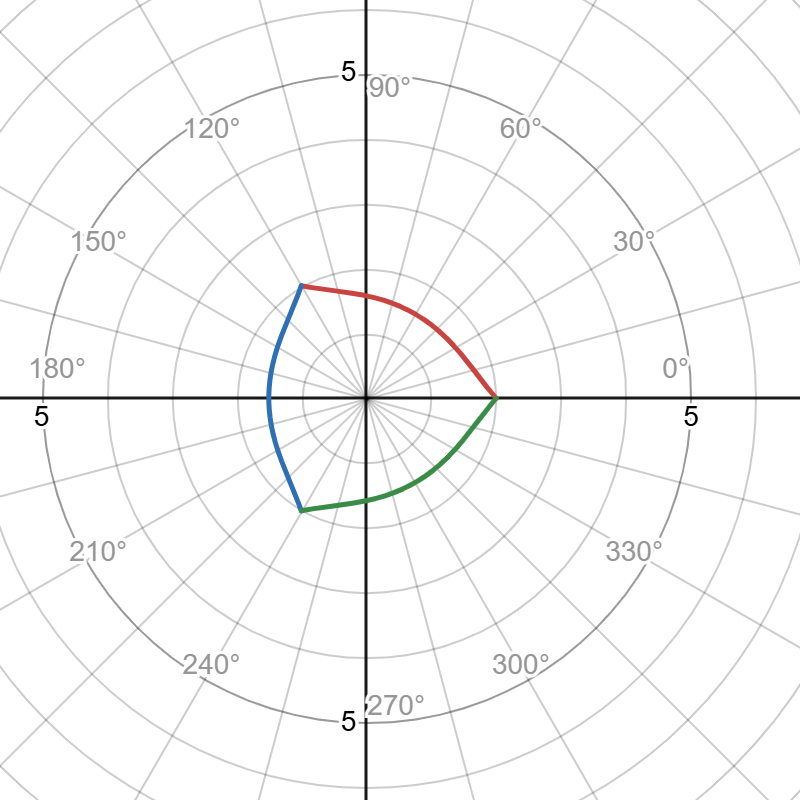正三角形＋１
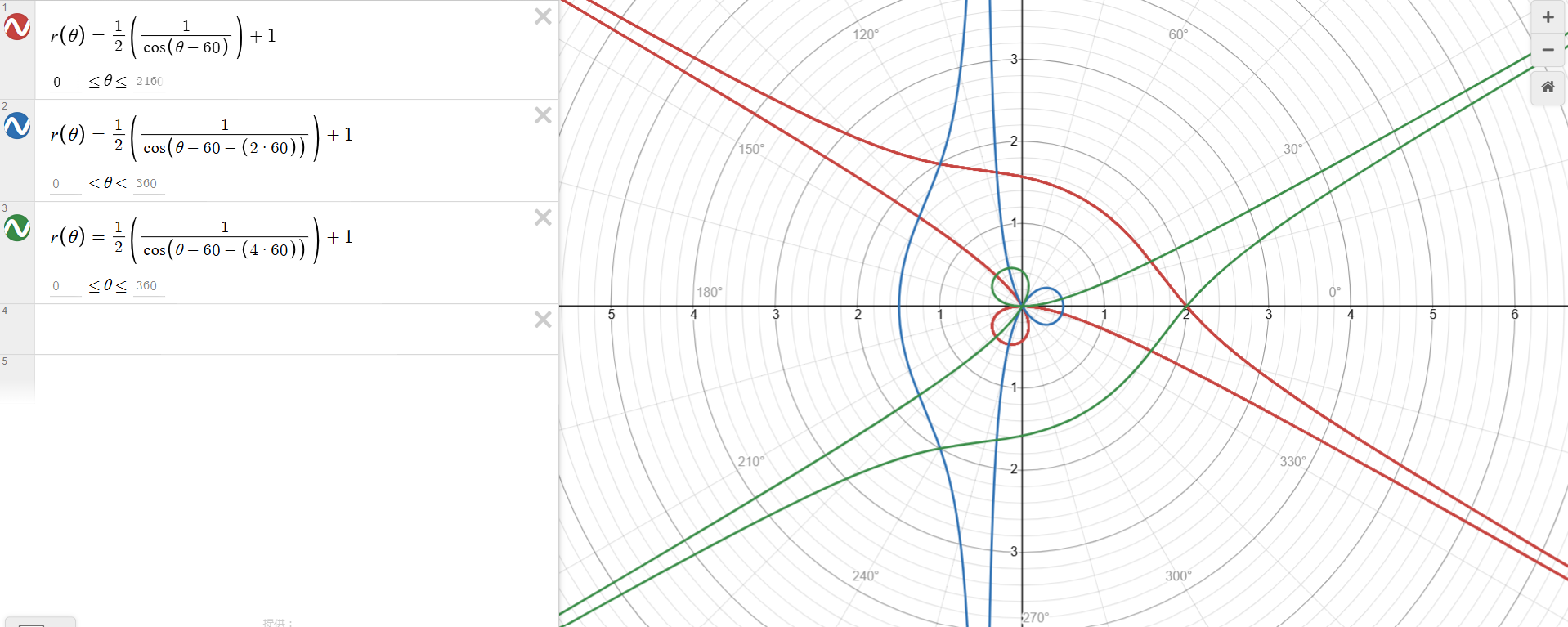正三角形+1（定義域決めずに）
結
これまでだらだら見づらいまま話してきましたが、もしこれをおもしろいと思っていただけたら、いろんな図形について極方程式を立てて、計算し、それを見せて頂けると幸いです。また、このようなアプローチはどうかというもの、誤字脱字の気づきがあれば、ご教授いただければ幸いです。ここまでお読みいただきありがとうございました。つぎは、楕円を離心率について、一般化した極方程式を立てたいと思っています。
資料
今回使用したグラフがこちらに入っていますので、ご参考になれば幸いです。
https://www.desmos.com/calculator/vfxlcpulxq
この記事を高評価した人
この記事に送られたバッジ
投稿者
