パステルカラーで保型形式を見る記事

この記事ではいくつかの保型形式(尖点形式)のグラフを眺めてみましょう．ふーん綺麗だな，と気楽に見てみてください．

また，$S_k(\Gamma_1(N))$の基底は，newformと呼ばれる特別な保型形式によって構成されます．その具体例を見てみましょう．この記事では主に1の用語や記法を用います．

グラフの描画について

まず保型形式とは正則な関数$f:\mathcal H\to \mathbb C$であって，ある種の対称性を持つものです．ただし$\mathcal H$は$\mathcal H:=\{\tau\in\mathbb C\mid \text{Im}\tau>0\}$で，複素平面の上半分の領域です．

$f:\mathcal H\to \mathbb C$のグラフは始域と終域がそれぞれ2次元的な広がりを持つので，グラフを描くことは普通にはできません．そこでこの記事では次のように工夫してグラフを描くことにします．

まず，次のように$\mathbb C$の各点にいい感じに色を割り振っておきます：
$\mathbb C$に色を割り振る

偏角が$-\pi$から$\pi$まで変化するとき，色は赤$\to$青$\to$黄$\to$赤と変化するようにしました．また，絶対値が小さいほど白に近い色になります．原点では白です．

関数$f:\mathcal H\to \mathbb C$が与えられたとき，位置$\tau\in\mathcal H$に$f(\tau)\in \mathbb C$に対応する色を置きます．これがこの記事における$f$のグラフです．

例えば，(これは保型形式ではありませんが)$f(\tau)=(\tau+1)(\tau-1-i)$の$\mathcal H$におけるグラフは次のようになります：
$f(\tau)=(\tau+1)(\tau-1-i)$

$\tau=-1,\;1+i$は$f$の零点なのでその2点ではグラフが白くなっていることが観察されます．

(この方法で複素関数のグラフを描くのは楽しいのでおすすめです．保型形式に限らず色々描いてみるといいと思います．私はプログラミングはそこまで詳しくないのですが，ChatGPTに相談しながらPythonで描画を行いました．)

レベル$13$のnewform

newformのグラフ

保型形式のうち特別なものはnewformと呼ばれます．重さ$2$，レベル$13$のnewformは2つあります．それらを見てみましょう．

1つは，次の$f_{13}$です．(2参照)：

$f_{13}(\tau)=q+(-\zeta_6-1)q^2+(2\zeta_6-2)q^3+\zeta_6q^4+(-2\zeta_6+1)q^5+\cdots$．

ただし，$\zeta_6$は$1$の原始$6$乗根$\zeta_6=\cos\dfrac{2\pi}{6}+i\sin\dfrac{2\pi}{6}$であり，$q=q(\tau)=e^{2\pi i\tau}$とおいています．

さて，$\sigma:\mathbb C\to \mathbb C$を複素共役を返す写像とします．$\sigma(\tau)=\overline\tau$．$f_{13}$の$q^n$の係数($a_n(f_{13})$と書くことにする)を$\sigma(a_n(f_{13}))$で置き換えたものを$f_{13}^\sigma$と書くことにすると，これもレベル$13$のnewformになります．$\overline{\zeta_6}=\zeta_6^{-1}$なので，

$f_{13}^\sigma(\tau)=q+(-\zeta_6^{-1}-1)q^2+(2\zeta_6^{-1}-2)q^3+\zeta_6^{-1}q^4+(-2\zeta_6^{-1}+1)q^5+\cdots$となります．

重さ$2$，レベル$13$のnewformは$f_{13},\;f_{13}^\sigma$の2つです．$\{f_{13},\;f_{13}^\sigma\}$は$S_2(\Gamma_1(13))^{new}(=S_2(\Gamma_1(13)))$の$\mathbb C$上の基底になっています．

これらのグラフを見てみましょう．
$f_{13}$
$f_{13}^\sigma$

まず，それぞれのグラフで$f_{13}(\tau+1)=f_{13}(\tau),\;f_{13}^\sigma(\tau+1)=f_{13}^\sigma(\tau)$となっていることが見てとれます．これは保型形式の持つ対称性の1つです．

また，2つのグラフの(色はさておき)形に注目すると$f_{13}$のグラフを虚軸に関して対称移動させたものが$f_{13}^\sigma$のグラフになっていることがわかります．このことには，$h:\mathcal H\to \mathcal H,\;a+bi\mapsto-a+bi$としたときに，$\overline q=\overline{e^{2\pi i\tau}}=e^{2\pi i h(\tau)}$となることから，$f_{13}^\sigma(\tau)=\sum \overline{a_n(f_{13})}q^n=\overline{\sum a_n(f_{13})\overline{q}^n}=\overline{f_{13}(h(\tau))}$という関係にあることが反映されています．

ヘッケ作用素を作用させる

一般に，正の整数$n$ごとにヘッケ作用素と呼ばれる$\mathbb C$上の線形写像$T_{n,(N)}:S_k(\Gamma_1(N))\to S_k(\Gamma_1(N))$があり，レベル$N$のnewformは$T_{n,(N)}$に関して非常に良い性質を持っています．

保型形式$f\in S_k(\Gamma_1(N))$の$q^n$の係数を$a_n(f)$と書くことにします：$f=\sum a_n(f)q^n$．このとき，$f$がレベル$N$のnewformであれば，$f$は$T_{n,(N)}$の固有ベクトルであり，その固有値は係数$a_n(f)$になるのです： $\forall n\in \mathbb Z^+,\; T_{n,(N)}f=a_n(f)f$．

固有ベクトルになるだけではなく，その固有値が係数に現れるというのはnewformの驚くべき性質です．

では先ほどの$f_{13}$を用いてヘッケ作用素の具体例を見てみましょう．
$T_{2,(13)}:S_2(\Gamma_1(13))\to S_2(\Gamma_1(13))$は一般の$f\in S_2(\Gamma_1(13))$に対して

$T_{2,(13)}f=\dfrac{1}{2}f(\dfrac{\tau}{2})+\dfrac{1}{2}f(\dfrac{\tau+1}{2})+\dfrac{2}{(26\tau+2)^2}f(\dfrac{14\tau+1}{26\tau+2})$と表せます．

この表示を用いて$T_{2,(13)}f_{13}$のグラフを描くと次のようになります：
$T_{2,(13)}f_{13}$

また，単に$a_2(f_{13})=-\zeta_6-1$倍した$(-\zeta_6-1)f_{13}$のグラフは次のようになります：
$(-\zeta_6-1)f_{13}$

近似値で描いているので少し違うのですが，この2つのグラフは似ていることがわかります．$T_{2,(13)}f_{13}=(-\zeta_6-1)f_{13}$となっていることが確認できました．

遠目に見るとけっこう似てる↓

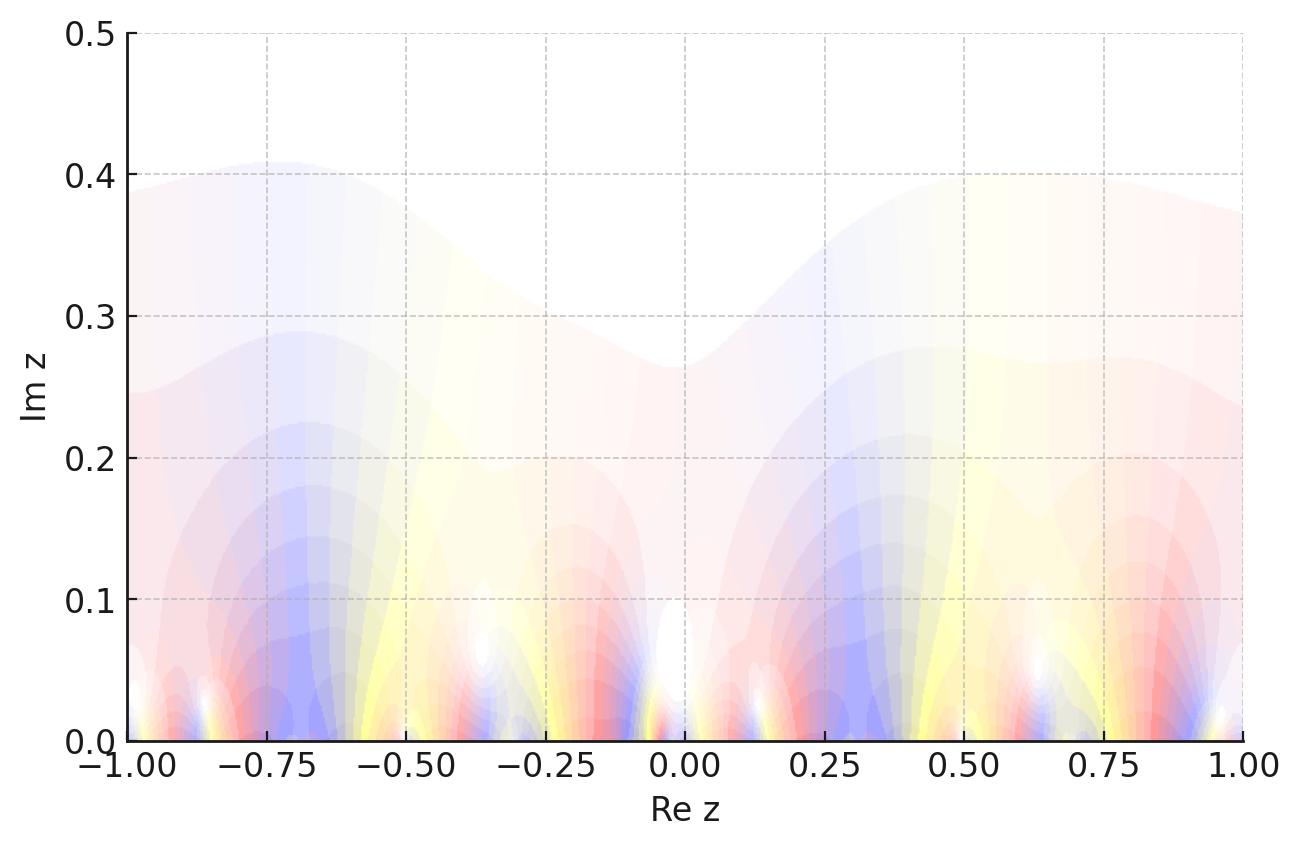
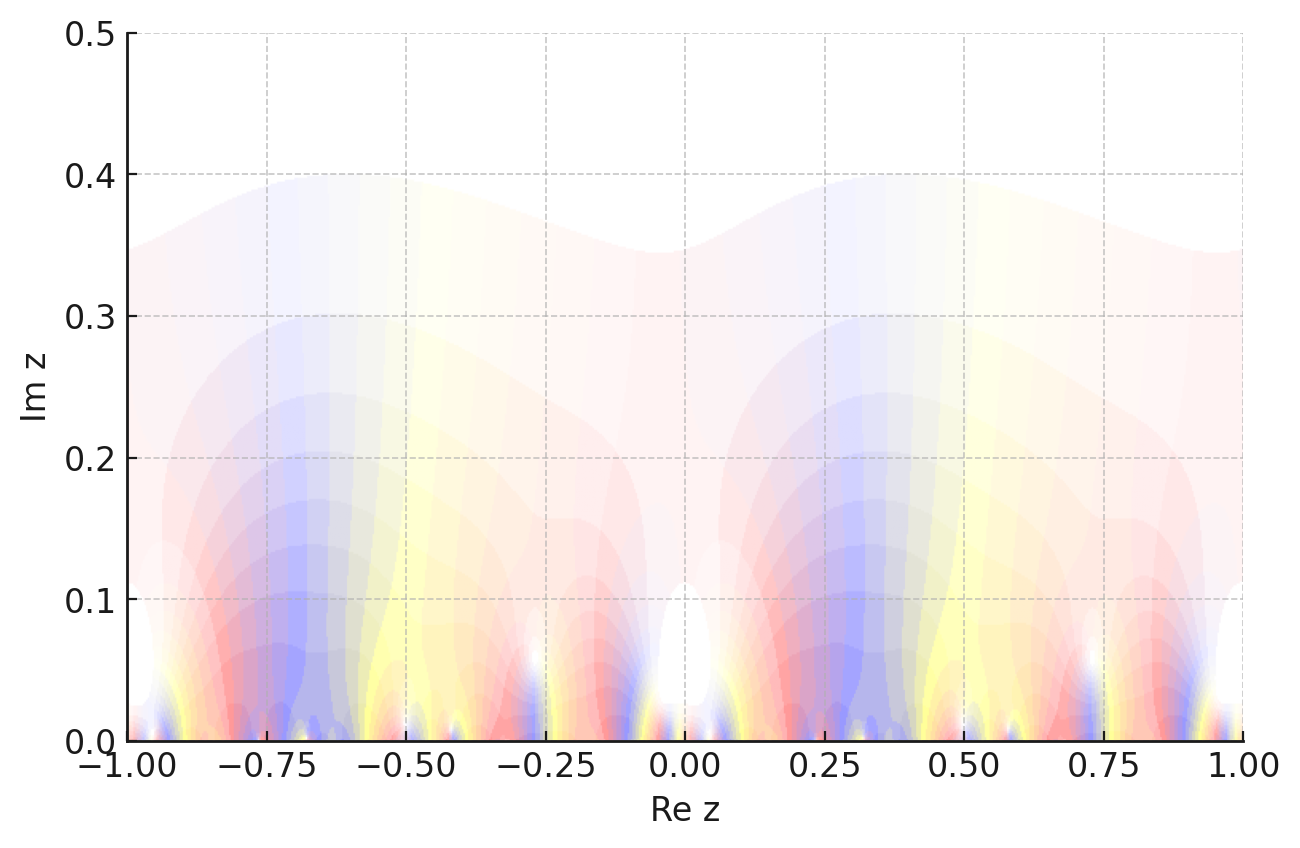
レベル$26$のnewform

newformのグラフ

レベル$26$のnewformを見てみましょう．レベル$26$のnewformは次の6個です．(2参照．)
$f_{26,1}=q-q^2+q^3+q^4-3q^5+\cdots$．
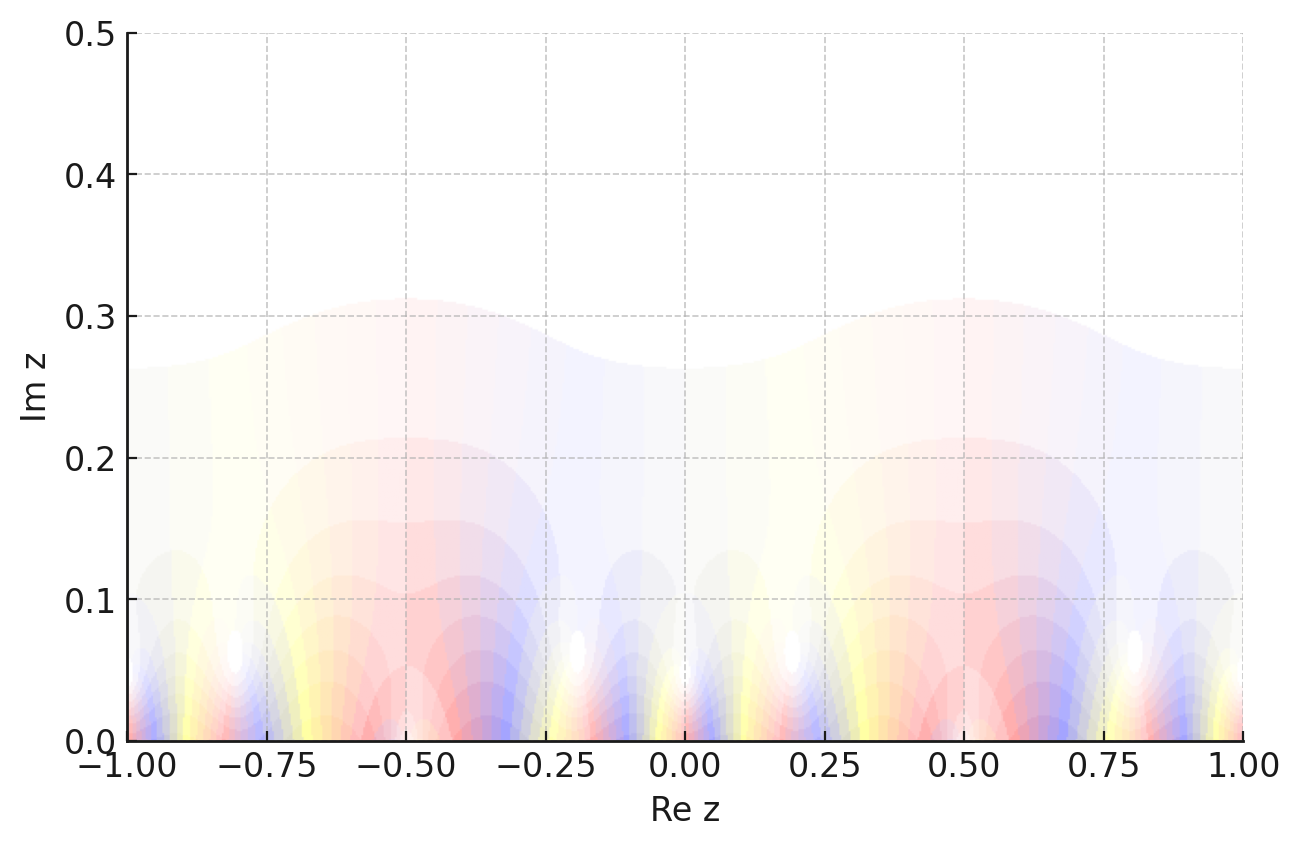f_{26,1}

$f_{26,2}=q+q^2-3q^3+q^4-q^5+\cdots$．
$f_{26,2}$

$f_{26,1},\;f_{26,2}$は$q^n$の係数が全て整数なので，さっきのレベル$13$のときの同様の考察により，$f_{26,j}(\tau)=\overline{f_{26,j}(h(\tau))}\;(j=1,2)$が得られ，(色はさておき)グラフの形だけ見ると，それぞれ虚軸に関して線対称になっていることがわかります．

$f_{26,3}=q+iq^2-q^3-q^4-3iq^5+\cdots$．
$f_{26,3}$

$f_{26,3}$の$q^n$の係数を複素共役で置き換えた$f_{26,3}^\sigma$．
$f_{26,3}^\sigma$

$f_{26,4}=q+(\zeta_6-1)q^2-\zeta_6 q^4-q^5+\cdots$．
$f_{26,4}$

$f_{26,4}$の$q^n$の係数を複素共役で置き換えた$f_{26,4}^\sigma$．

$f_{26,4}^\sigma$

$S_2(\Gamma_1(26))$の基底

重さ$2$，レベル$26$のnewformは$f_{26,1},\;f_{26,2},\;f_{26,3},\;f_{26,3}^\sigma,\;f_{26,4},\;f_{26,4}^\sigma$の6個です．

$\{f_{26,1},\;f_{26,2},\;f_{26,3},\;f_{26,3}^\sigma,\;f_{26,4},\;f_{26,4}^\sigma\}$

は$S_2(\Gamma_1(26))^{new}$の$\mathbb C$上の基底になっています．

ここにレベル$13$のnewformから作られる$f_{13},\;f_{13}(2\tau),\;f_{13}^\sigma,\;f_{13}^\sigma(2\tau)$の4つを加えた

$\{f_{26,1},\;f_{26,2},\;f_{26,3},\;f_{26,3}^\sigma,\;f_{26,4},\;f_{26,4}^\sigma,\;f_{13},\;f_{13}(2\tau),\;f_{13}^\sigma,\;f_{13}^\sigma(2\tau)\}$

が$S_2(\Gamma_1(26))$の基底になります．

実は一般に$S_k(\Gamma_1(N))$の基底はレベルが$N$の約数であるようなnewformたちによって構成されるのです．

本の紹介

今，私は『A First Course in Modular Forms』1を読んでいます．最初は$M_k(\Gamma)$や$S_k(\Gamma)$がどんな線形空間かイメージがつかなったのですが，読み進めると実はその基底はけっこう明示的に表せることがわかり，グラフを描いたりしてそれらに馴染んできました．特に$S_k(\Gamma_1(N))$の基底はnewformたちで記述できるのが美しいと思います．

まだ本の途中なのですが，イメージがわかなかったものがだんだんクリアになってくる楽しい本です．英語で書かれていますが，最後まで頑張って読みたいと思います．おしまい