Airy関数の一般化２：C-両側Laplace変換と高階Airy関数

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

前書き

前回の記事で、基本解を得ることができました。
今回は、もっといい性質を持つような解を構成していきます。
この記事では$\mu,\nu$は常に正整数とし、$\zeta_\omega=e^{2\pi i/\omega}$と記すことにします。
複素変数のグラフのメモリは正確ではないです。

$C$-両側Laplace変換

$s\in\mathbb{C}$に対して、第一種Airy関数は次のように定義されます。
$$\Ai{s}=\frac{1}{2\pi i}\int_{e^{-\pi i/3}\infty}^{e^{\pi i/3}\infty}e^{x^3/3-sx}dx=\frac{1}{2\pi i}\int_{e^{-2\pi i/3}\infty}^{e^{2\pi i/3}\infty}e^{-x^3/3+sx}dx$$
これは$e^{x^3/3}\in\Om{1}{2},e^{-x^3/3}\in\Ombar{1}{2}$という関数を使って$\Om{2}{1}$の解が構成できているということですね。
この方法を一般化することを考えましょう。

$C$-両側Laplace変換

関数$f$と、$f$が両端で消えているような経路$C$に対して、$C$-両側Laplace変換を次のように定めます。
$$\B{f(x)}{s}=\int_Ce^{-sx}f(x)dx $$
$$\Bstar{f(x)}{s}=\int_Ce^{sx}f(x)dx $$

通常の両側Laplace変換と逆両側Laplace変換を一般の経路に関して拡張した感じですね。
ただし、$\mathcal{B}_C$と$\mathcal{B}^*_C$は互いの逆変換になっていないことに注意しましょう。

部分積分を使うと、こんな性質が成り立つことがわかります。

階数と次数を入れ替える

$$\B{D^\mu f(x)}{s}=s^\mu\B{f(x)}{s}$$
$$\B{x^\nu f(x)}{s}=(-D)^\nu\B{f(x)}{s}$$
$$\Bstar{D^\mu f(x)}{s}=(-s)^\mu\B{f(x)}{s}$$
$$\Bstar{x^\nu f(x)}{s}=D^\nu\B{f(x)}{s}$$

この変換を多項式係数の線形微分方程式の両辺に施すことを考えると、
$\mathcal{B}:D\mapsto x,x\mapsto-D $
$\mathcal{B}^*:D\mapsto-x,x\mapsto D$
という置換になります。
$Dx-xD=1$に注意して、各項について$D$が右側に来るように整理すればこれは新たな微分方程式になります。

双対方程式

多項式係数の線形微分方程式$E$に対して、$\mathcal{B}:D\mapsto x,x\mapsto-D$という変換を施して得られる新しい方程式を、$\mathcal{B}E$と記し、$E$の双対方程式と呼ぶことにします。

同様に、$\mathcal{B}^*:D\mapsto-x,x\mapsto D$という変換を施して得られる方程式を$\mathcal{B}^*E$と記し、これも$E$の双対方程式と呼びます。

双対方程式の解を用いて、元の方程式の解を記述できます。

$C$-両側Laplace変換を用いた解の表示

$y\in\mathcal{B}E$とすると、$\Bstar{y}{s}$は$E$の解となる。同様に、$y^*\in\mathcal{B}^*E$とすると、$\B{y^*}{s}$は$E$の解となる。

これは$\mathcal{B}$と$\mathcal{B}^*$が方程式への作用に関して逆変換になっていることからくる性質です。
また、この手法は有界な解を得る方法も与えてくれます。

定理２において$C$を虚軸にすることができれば、$\Bstar{y}{s},\B{y^*}{s}$は$E$の実軸上有界な解となる。

Riemann–Lebesgueの補題からの帰結です。
ほかにも、ある方向で有界な解を得たければそれに直交する経路を取ればいいこともわかります。
$C^\top$を$C$に直交する経路とすると、$\mathcal{B}_C \circ\mathcal{B}^*_{C^\top}= \mathcal{B}^*_{C^\top}\circ\mathcal{B}_C=2\pi i\;\mathrm{id} $となるということですね。

蛇足ですが、これは微分方程式をWeyl代数$A_1(\mathbb{C})=\mathbb{C}[x,D]/(Dx-xD-1)$の元とみなして、
写像$\mathcal{B}:A_1(\mathbb{C})\to A_1(\mathbb{C})$を生成元に関する関係式$\mathcal{B}(x)=-D,\mathcal{B}(D)=x$で定めています。
これは演算と整合的で$\mathbb{C}$の元を動かしません。そして$\mathcal{B} ^4=\mathrm{id}$となるので$\mathbb{C}$同型になります。
これは$\mathbb{C}[[x,D]]/(Dx-xD-1)$に一意拡張できるので、実は差分方程式を解くのに使えたりもします。

この手法を用いて実際に解を構成しましょう！

高階Airy関数の定義

$\Om{\mu}{1}:D^\mu y=xy$の有界な解を得ることを考えます。

$\mathcal{B}\Om{\mu}{1}=\Ombar{1}{\mu}$なので、$\Bstar{e^{-x^\omega/\omega}}{s}\in\Om{\mu}{1}$となります。
そこで、どのように$C$を選べばいいか考えましょう。$e^{-x^\omega/\omega}$のグラフを見てみます。
!FORMULA[58][112342475][0] $e^{-x^\omega/\omega}\;\;(\omega=2,...,9)$
白い部分を避けて経路を引く必要があります。収束するセクターと虚軸の関係はmod4で分類できますね。
$\omega\equiv0$：虚軸は収束セクターの内側に含まれている
$\omega\equiv1$：虚軸は収束セクターの左側に触れている
$\omega\equiv2$：経路を虚軸に沿わせることはできない
$\omega\equiv3$：虚軸は収束セクターの右側に触れている
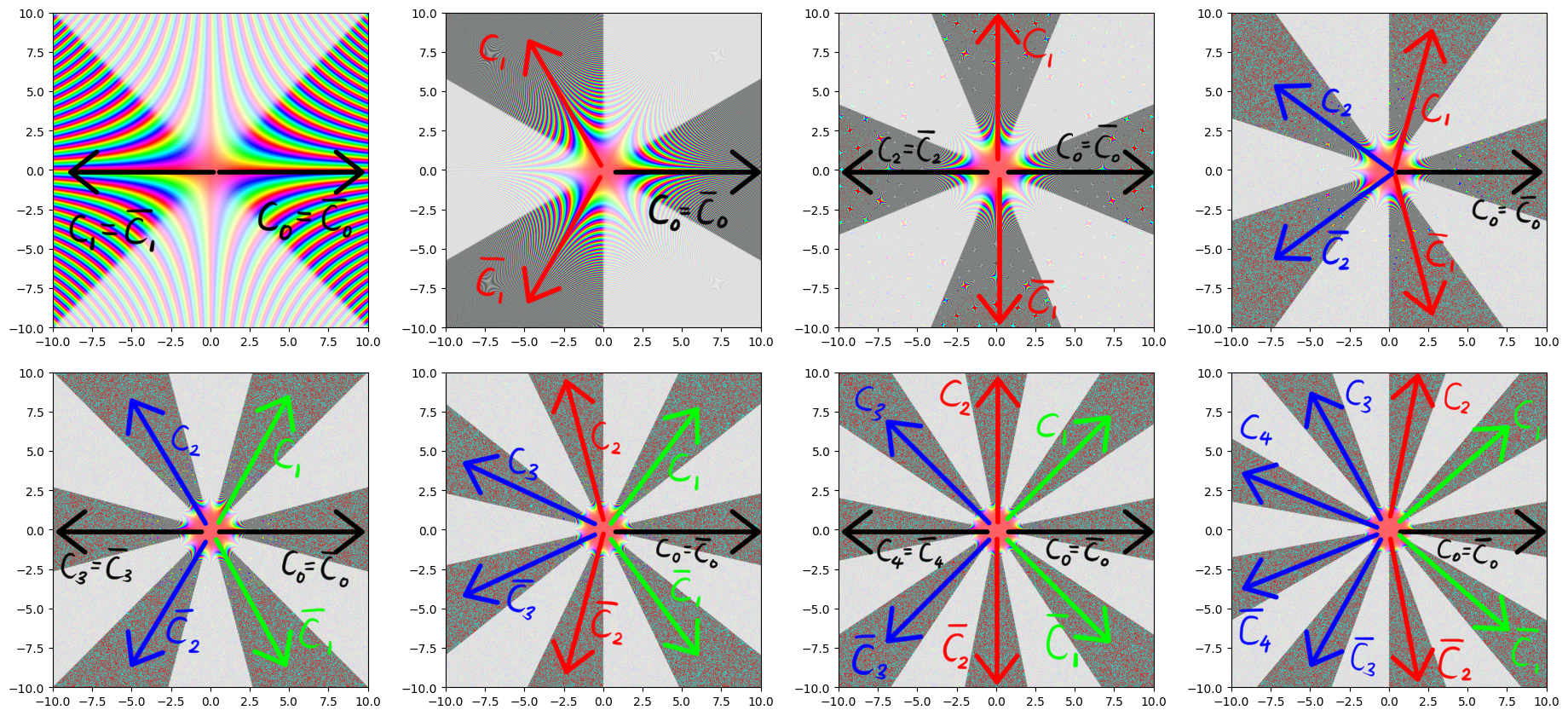経路の取り方
虚軸に接するセクターの経路を赤、右半平面の経路を緑、左半平面の経路を青、実軸を含むセクターの経路を黒で書いています。ごちゃごちゃしているのでこれ以上書きませんが、要領はつかめたと思います。
$C_n:x=\zeta_\omega^nt\:$ $\bar{C}_n:x=\zeta_\omega^{-n}t$ $(0< t<\infty)$
という風に書けますね。経路はセクターを跨がない限り自由に変形しても大丈夫です。
$C_n$と$\bar{C}_n$は$n\neq0$の時共役な経路になっているので、これらを足し引きすれば実軸上で実数値をとる関数が得られます。

高階Airy関数

$1$次の高階Airy関数を次のように定義します。
$$\Aimu{\mu}{n,s}=\frac{1}{2\pi i}\int_{C_n-\bar{C}_n}e^{-x^\omega/\omega+sx}dx$$
$$\Bimu{\mu}{n\to m,s}=\frac{1}{2\pi}\int_{C_m+\bar{C}_m-C_n-\bar{C}_n}e^{-x^\omega/\omega+sx}dx$$
$m=0$のときは矢印を省略して$\Bimu{\mu}{n,s}$と書くことにします。

$\mu=1,2$のときは次のようになります。
$$\Bimu{1}{1,s}=\sqrt{\frac{2}{\pi}}e^{s^2/2}\:,\mathrm{Ai}^2(1,s)=\mathrm{Ai}(s)\:,\mathrm{Bi}^2(1,s)=\mathrm{Bi}(s)$$

実部・虚部を使った表示

$$\mathrm{Ai}^\mu(n,s)=\frac{1}{\pi}\mathfrak{I}\int_{0}^{\infty}e^{-x^\omega/\omega+\zeta_\omega^nsx}\zeta_\omega^ndx$$
$$\mathrm{Bi}^\mu(n\to m,s)=\frac{1}{\pi}\mathfrak{R}\left(\int_0^\infty e^{-x^\omega/\omega+\zeta_\omega^msx}\zeta_\omega^mdx-\int_{0}^{\infty}e^{-x^\omega/\omega+\zeta_\omega^nsx}\zeta_\omega^ndx\right)$$

変数変換しただけです。こう表せるように定義したんでしたね。
この表示を使ってこれらの関数の高階導関数の$0$での値を求めて次を得ます。

級数表示

前回の記事の定理２系より、
$$\mathrm{Ai}^\mu(n,x)=\frac{1}{\pi\omega}\sum_{k=0}^{\mu-1}\omega^{(k+1)/\omega}\sin\left(\frac{2\pi n(k+1)}{\omega}\right)\Gamma\left(\frac{k+1}{\omega}\right)\Omega_{\mu 1k}(x)$$
$$\mathrm{Bi}^\mu(n\to m,x)=\frac{1}{\pi\omega}\sum_{k=0}^{\mu-1}\omega^{(k+1)/\omega}\left(\cos\left(\frac{2\pi m(k+1)}{\omega}\right)-\cos\left(\frac{2\pi n(k+1)}{\omega}\right)\right)\Gamma\left(\frac{k+1}{\omega}\right)\Omega_{\mu 1k}(x)$$

これらの関数の中で最も重要な関数は、経路を虚軸に変形できるものです。
これはセクターが虚軸を含む、もしくは接しているとき（つまり$\omega\cancel{\equiv}2\mod4$のとき）存在します。

有界な関数

$C_n$が虚軸に接するセクターに含まれるとき、$\Aimu{\mu}{n,s}$は実軸上有界な関数になる。
これを単に$\Aimu{\mu}{s}$と記す。ついでに同じ$n$に対して$\Bimu{\mu}{n,s}$を$\Bimu{\mu}{s}$と記すことにする。

実変数の積分表示

$s\in\mathbb{C}$に対して、次が成り立つ。
・$\omega \equiv 0\mod4$のとき：
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{\pi}\int_0^\infty e^{-x^\omega/\omega}\cos(sx)dx \end{align*}$$

また、$s\in\mathbb{R}$に対して、次が成り立つ。
・$\omega \equiv 1\mod4$のとき：
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{\pi }\int_{0}^{\infty} \cos\left(\frac{x^\omega}{\omega}-sx\right)dx \end{align*}$$
・$\omega \equiv 3\mod4$のとき：
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{\pi }\int_{0}^{\infty} \cos\left(\frac{x^\omega}{\omega}+sx\right)dx \end{align*}$$

経路の極限を取って示す

・$\omega \equiv 0\mod4$
この場合、虚軸は収束セクターの中心にあるので、問題なく積分路に虚軸を選べて次のようになります。
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{2\pi i}\int_{-i\infty}^{i\infty} e^{-x^\omega/\omega+sx}dx=\frac{1}{\pi}\int_0^\infty e^{-x^\omega/\omega}\cos(sx)dx \end{align*}$$
・$\omega \equiv 1\mod4$
先程ほど簡単にはいきません。虚軸はセクターの左側にあります。そこで$\epsilon>0$を使って、
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{2\pi i}\int_{-i\infty+\epsilon}^{i\infty+\epsilon} e^{-x^\omega/\omega+sx}dx=\frac{1}{2\pi }\int_{-\infty-i\epsilon}^{\infty-i\epsilon} e^{-ix^\omega/\omega+isx}dx\\ &=\frac{1}{2\pi }\int_{-\infty-i\epsilon}^{\infty-i\epsilon} \cos\left(\frac{x^\omega}{\omega}-sx\right)dx-\frac{1}{2\pi }\int_{-\infty-i\epsilon}^{\infty-i\epsilon} \sin\left(\frac{x^\omega}{\omega}-sx\right)dx \end{align*}$$
$\epsilon\rightarrow 0$とすれば次を得ます。ただしこれは$s$が実数の時しか収束しません。
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{\pi }\int_{0}^{\infty} \cos\left(\frac{x^\omega}{\omega}-sx\right)dx \end{align*}$$
・$\omega \equiv 3\mod4$
先ほどと逆で、虚軸はセクターの左に触れています。$\epsilon$の符号を変えて同じように計算すれば、
$$\begin{align*}\mathrm{Ai}^\mu(s)&=\frac{1}{\pi }\int_{0}^{\infty} \cos\left(\frac{x^\omega}{\omega}+sx\right)dx \end{align*}$$
が得られます。

このように、関数の挙動を決定するのは経路がどのセクターを通るかで決定されます。

$C_n$が左（右）半平面にあるセクターに含まれるとき、$n:left$（$n:right$）と記すことにしましょう。
このとき、虚軸に接するセクターは左右両方に含まれると解釈してください。
公式１の表示により、次のようなことが言えます。

収束の雰囲気

-実軸上有界な関数
$$\mathrm{Ai}^\mu(s)$$
-正の実軸で収束する関数（$n,m:left$）
$$\mathrm{Ai}^\mu(n,s),\mathrm{Bi}^\mu(n\rightarrow m,s)$$
-負の実軸で収束する関数（$n,m:right$）
$$\mathrm{Ai}^\mu(n,s),\mathrm{Bi}^\mu(n\rightarrow m,s)$$

$\Bimu{\mu}{n\to m,s}$を使うときは、経路を左から右に取ると$0$での値が正になって少しうれしいです。
実軸上よく振舞う解が得られました。これらの関数の例を見てみましょう。

高階Airy関数の例

$\mu=1,2$のとき、既知の関数で表せるのでした。では、より高階の場合を見ていきましょう。

$\Om{3}{1}$の解

$\Aimu{3}{s},\Bimu{3}{s},\Bimu{3}{-s}$は実軸上もっともよく振舞う$\Om{3}{1}$の基本解となる。

!FORMULA[121][315881673][0]のグラフ $\Aimu{3}{s},\Bimu{3}{s},\Bimu{3}{-s}$のグラフ
これは$\Bimu{3}{2\to1,s}=\Bimu{3}{-s}$となるからですね。
これらが線形独立であることはセクターを跨がずに経路をほかの関数の経路に変形できないことから従います。

いくつかの性質

$$\mathrm{Ai}^3(x)=\frac{\Gamma(1/4)}{2\sqrt{2}\pi}\Omega_{310}(x)-\frac{\Gamma(3/4)}{\sqrt{2}\pi}\Omega_{312}(x)$$
$$\mathrm{Bi}^3(x)=\frac{\Gamma(1/4)}{2\sqrt{2}\pi}\Omega_{310}(x)+\frac{1}{\sqrt{\pi}}\Omega_{311}(x)+\frac{\Gamma(3/4)}{\sqrt{2}\pi}\Omega_{312}(x)$$
$$\mathrm{Bi}^3(-x)=\frac{\Gamma(1/4)}{2\sqrt{2}\pi}\Omega_{310}(x)-\frac{1}{\sqrt{\pi}}\Omega_{311}(x)+\frac{\Gamma(3/4)}{\sqrt{2}\pi}\Omega_{312}(x)$$

$$\mathcal{W}(\mathrm{Ai}^3(x),\mathrm{Bi}^3(x),\mathrm{Bi}^3(-x))=\frac{\sqrt{2}}{\pi^{3/2}}$$
$$\int_{-\infty}^\infty\Aimu{3}{x}dx=1\:,\:\:\int_{0}^\infty\Aimu{3}{x}dx=\frac12\:,\:\:\int_{-\infty}^0\Bimu{3}{x}dx=0$$
$$\int_{-\infty}^\infty e^{sx}\Aimu{3}{x}dx=e^{-s^4/4}$$
$$\int_0^\infty e^{-sx}\mathrm{Ai}^3(x)dx=\frac{e^{-s^4/4}}{2}\left(1+ \frac{s^3}{3\Gamma(3/4)}{}_{1}F_{1}\left[\begin{matrix}3/4\\7/4\end{matrix};\frac{s^4}{4}\right]-\frac{2s}{\Gamma(1/4)}{}_{1}F_{1}\left[\begin{matrix}1/4\\5/4\end{matrix};\frac{s^4}{4}\right]\right)$$
$$\int_0^\infty e^{-sx}\mathrm{Bi}^3(-x)dx=e^{-s^4/4}\left( \frac{s^3}{6\Gamma(3/4)}{}_{1}F_{1}\left[\begin{matrix}3/4\\7/4\end{matrix};\frac{s^4}{4}\right]+\frac{s^2}{2\sqrt{\pi}}{}_{1}F_{1}\left[\begin{matrix}3/4\\7/4\end{matrix};\frac{s^4}{4}\right]+\frac{s}{\Gamma(1/4)}{}_{1}F_{1}\left[\begin{matrix}1/4\\5/4\end{matrix};\frac{s^4}{4}\right]\right)$$
$$\int_0^\infty x^{s-1}\mathrm{Ai}^3(x)dx=\frac{2^\frac{1-s}{2}}{4\pi}\Gamma(s)\Gamma\left(\frac{1-s}{4}\right)\cos\left(\frac{\pi s}{2}\right)$$
$$\int_0^\infty x^{s-1}\mathrm{Bi}^3(-x)dx=\frac{2^\frac{1-s}{2}}{4\pi}\Gamma(s)\Gamma\left(\frac{1-s}{4}\right)\left(1-\sin\left(\frac{\pi s}{2}\right)\right)$$
$$2\Aimu{3}{ix}=\Bimu{3}{x}+\Bimu{3}{-x}$$
$$\int_{-\infty}^{\infty}\Aimu{3}{x+s}\Aimu{3}{x+s'}dx=\frac{1}{2^{1/4}}\Aimu{3}{\frac{s-s'}{2^{1/4}}}$$

これらの性質は以前の結果を当てはめるだけ、もしくは次章で一般の場合について示すのでここでは証明しません。

$\Om{4}{1}$の解

$\Aimu{4}{s},\Bimu{4}{s},\Aimu{4}{2,s},\Bimu{4}{2\to1,s}$は実軸上もっともよく振舞う$\Om{4}{1}$の基本解となる。

!FORMULA[138][2064527328][0]のグラフ $\Aimu{4}{s},\Bimu{4}{s},\Aimu{4}{2,s},\Bimu{4}{2\to1,s}$のグラフ

先ほどよりもAiry関数感がありますね。先ほどと同じ理由で基本解になっています。
$\Bimu{4}{2,s}$ではなく$\Bimu{4}{2\to1,s}$を使ったのは経路を左半平面にとるためです。

いくつかの性質

$$\mathcal{W}(\Aimu{4}{s},\Bimu{4}{s},\Aimu{4}{2,s},\Bimu{4}{2\to1,s})=\frac{1}{\pi^2}$$
$$\int_{-\infty}^\infty\Aimu{4}{x}dx=1\:,\:\:\int_{0}^\infty\Aimu{4}{x}dx=\frac35\:,\:\:\int_{-\infty}^0\Aimu{4}{x}dx=\frac25$$
$$\int_{0}^\infty\Aimu{4}{2,x}dx=\frac15\:,\:\:\int_{0}^\infty\Bimu{4}{2\to1,x}dx=0\:,\:\:\int_{-\infty}^0\Bimu{4}{x}dx=0$$
$$\int_{-\infty}^\infty e^{-sx}\Aimu{4}{x}dx=e^{-s^5/5}$$
$$\int_{-\infty}^{\infty}\Aimu{4}{x+s}\Aimu{4}{x+s'}dx=\delta(s-s')$$

片側Laplace変換やMellin変換は煩雑になるので省略しました。
先ほどよりもAiry関数との類似性が見て取れますね。

$\Om{5}{1}$の解

$\Aimu{5}{1,s},\Bimu{5}{1,s},\Aimu{5}{1,-s},\Bimu{5}{1,-s},\Bimu{5}{3\to0,s}$は実軸上もっともよく振舞う$\Om{5}{1}$の基本解となる。

!FORMULA[149][-442314239][0]のグラフ $\Aimu{5}{1,s},\Bimu{5}{1,s},\Aimu{5}{1,-s},\Bimu{5}{1,-s},\Bimu{5}{3\to0,s}$のグラフ
先ほど見た通り、$6\equiv2\mod4$なので有界な解は存在しません。
一方、$\Aimu{5}{2,s}=\Aimu{5}{1,-s},\Bimu{5}{3\to2,s}=\Bimu{5}{1,-s}$となるので３種類の関数で基本解を構成できます。
注目すべきは、$\Bimu{5}{3\to0,is}$が$\Ombar{5}{1}$の有界な解になっている点ですね。

いくつかの性質

$$\mathcal{W}(\Aimu{5}{1,s},\Bimu{5}{1,s},\Aimu{5}{1,-s},\Bimu{5}{1,-s},\Bimu{5}{3\to0,s})=\frac{\sqrt{2}}{\pi^{5/2}}$$
$$\int_{0}^\infty\Aimu{5}{1,-x}dx=\frac13\:,\:\:\int_{0}^\infty\Bimu{5}{1,-x}dx=0\:,\:\:\int_{-\infty}^0\Bimu{4}{x}dx=0$$

通常のAiry関数の場合も含めてこれで$\mod4$で一つずつ例を見ました。
次に一般の場合に成り立つ性質を見ていきましょう。

高階Airy関数の性質

ここではAiry関数の様々な性質を高階Airy関数に一般化していきます。
どんな式を一般化したのかわかるように毎回Airy関数に関する式も書いています。

Airy関数の積分

$$\int_{-\infty}^{\infty}\Ai{x}dx=1$$
$$\int_{0}^{\infty}\Ai{x}dx=\frac13$$
$$\int_{-\infty}^{0}\Ai{x}dx=\frac23$$

高階Airy関数の積分

$$\int_{-\infty}^{\infty}\Aimu{\mu}{x}dx=1$$

$$\int_{0}^{\infty}\mathrm{Ai}^\mu(s)ds= \begin{eqnarray} \left\{ \begin{array}{l} \frac{1}{2}\left(1-\frac{1}{\omega}\right)\:\:(\omega\equiv3\mod4) \\ \frac{1}{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(\omega\equiv0\mod4)\\ \frac{1}{2}\left(1+\frac{1}{\omega}\right)\:\:(\omega\equiv1\mod4) \\ \end{array} \right. \end{eqnarray} $$
$$\int_{-\infty}^{0}\mathrm{Ai}^\mu(s)ds= \begin{eqnarray} \left\{ \begin{array}{l} \frac{1}{2}\left(1+\frac{1}{\omega}\right)\:\:(\omega\equiv3\mod4) \\ \frac{1}{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:(\omega\equiv0\mod4)\\ \frac{1}{2}\left(1-\frac{1}{\omega}\right)\:\:(\omega\equiv1\mod4) \\ \end{array} \right. \end{eqnarray} $$

デルタ関数でごり押し

$$\mathrm{Ai}^\mu(s)=\frac{1}{2\pi i}\int_{-i\infty}^{i\infty}e^{-x^\omega/\omega+sx}dx=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{-i^\omega x^\omega/\omega+isx}dx$$
と書けばデルタ関数を使って次のように計算できる
$$\begin{align*}\int_{-\infty}^{\infty}\mathrm{Ai}^\mu(s)ds&=\int_{-\infty}^{\infty}\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{-i^\omega x^\omega/\omega+isx}dxds\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{-i^\omega x^\omega/\omega}2\pi\delta(x)dx=1 \end{align*}$$
同様に
$$\begin{align*}\int_{0}^{\infty}\mathrm{Ai}^\mu(s)ds&=\int_{0}^{\infty}\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{-i^\omega x^\omega/\omega+isx}dxds\\ &=\frac{1}{2\pi}p.v.\int_{-\infty}^{\infty}e^{-i^\omega x^\omega/\omega}\left(\pi\delta(x)-\frac{1}{ix}\right)dx\\ &=\frac{1}{2}-\frac{1}{\pi}p.v.\int_0^\infty\frac{e^{-i^\omega x^\omega/\omega}}{ix}dx \end{align*}$$
ここで$\omega\equiv0\mod4$なら最後のコーシー主値は消え答えは$1/2$になる
$\omega\equiv3\mod4$なら答えは
$$\frac{1}{2}-\frac{1}{\pi}\int_0^\infty\frac{\sin(x^\omega/\omega)}{x}dx=\frac{1}{2}\left(1-\frac{1}{\omega}\right)$$
となる。$\omega\equiv1\mod4$の時は符号が変わるだけである

Airy関数の両側Laplace変換

$\mathfrak{R}s\leq0$のとき、次が成り立つ
$$\int_{-\infty}^{\infty}e^{-sx}\Ai{x}dx=e^{-s^3/3}$$

高階Airy関数の両側Laplace変換

適切な$s$（$\omega\equiv0$なら$s\in\mathbb{C}$、$\omega\equiv1$なら$\mathfrak{R}s\geq0$、$\omega\equiv3$なら$\mathfrak{R}s\leq0$）について、次が成り立つ
$$\int_{-\infty}^{\infty}e^{-sx}\Aimu{\mu}{x}dx=e^{-s^\omega/\omega}$$

$\mathcal{B}^*\Ombar{1}{\mu}=\Om{\mu}{1}$の解として$\Aimu{\mu}{x}$を取り、経路として実軸を取ると、
$$\int_{-\infty}^{\infty}e^{-sx}\Aimu{\mu}{x}dx=ce^{-s^\omega/\omega} $$
は$\Ombar{1}{\mu}$の解となるので、$s=0$とすれば定理８より$c=1$とわかります。

Airy関数の片側Laplace変換

$$\int_0^\infty e^{-sx}\Ai{x}dx=e^{-s^3/3}\left(\frac13-\frac{s}{3^{1/3}\Gamma(1/3)}{}_{1}F_{1}\left[\begin{matrix}1/3\\4/3\end{matrix};\frac{s^3}{3}\right]+\frac{s^2}{2 \cdot 3^{2/3}\Gamma(2/3)}{}_{1}F_{1}\left[\begin{matrix}2/3\\5/3\end{matrix};\frac{s^3}{3}\right]\right)$$

高階Airy関数の片側Laplace変換

$\Omega$が$\Om{\mu}{1}$の解で、$\int_0^\infty\Omega(x)dx$が存在するとき、次が成り立つ。
$$\int_0^\infty e^{-sx}\Omega(x)dx=e^{-s^\omega/\omega}\left(\int_0^\infty\Omega(x)dx+\sum_{n=1}^{\mu}\frac{s^n}{n}{}_{1}F_{1}\left[\begin{matrix}n/\omega\\1+n/\omega\end{matrix};\frac{s^\omega}{\omega}\right]\Omega^{(\mu-n)}(0)\right)$$

この片側Laplace変換を$s$で微分して部分積分を繰り返せば、一階の非斉次微分方程式：
$$Dy+x^\mu y=\sum_{n=0}^{\mu-1}x^n\Omega^{\mu-n-1}(0)$$
の解になっていることが分かるので、これを解いて$s=0$で定数を決定すればいいです。

Airy関数のMellin変換

$$\int_0^\infty x^{s-1}\Ai{x}dx=\frac{3^\frac{1-s}{3}}{3\pi}\Gamma(s)\Gamma\left(\frac{1-s}{3}\right)\cos\left(\frac{\pi s}{2}+\frac{\pi}{2}\frac{1-s}{3}\right)$$
$$\int_0^\infty x^{s-1}\Ai{-x}dx=\frac{3^\frac{1-s}{3}}{3\pi}\Gamma(s)\Gamma\left(\frac{1-s}{3}\right)\cos\left(\frac{\pi s}{2}-\frac{\pi}{2}\frac{1-s}{3}\right)$$

高階Airy関数のMellin変換

$f(s)=\frac{\omega^\frac{1-s}{\omega}}{\omega\pi}\Gamma(s)\Gamma(\frac{1-s}{\omega})$とすると、$n,m:left$について次が成り立つ。
$$\int_0^\infty x^{s-1}\Aimu{\mu}{n,x}dx=f(s)\sin\left(\frac{2\pi n(1-s)}{\omega}+\pi s\right)$$
$$\int_0^\infty x^{s-1}\Bimu{\mu}{n\to m,x}dx=f(s)\left(\cos\left(\frac{2\pi m(1-s)}{\omega}+\pi s\right)-\cos\left(\frac{2\pi n(1-s)}{\omega}+\pi s\right)\right)$$
また、$n,m:right$について次が成り立つ。
$$\int_0^\infty x^{s-1}\Aimu{\mu}{n,-x}dx=f(s)\sin\left(\frac{2\pi n(1-s)}{\omega}\right)$$
$$\int_0^\infty x^{s-1}\Bimu{\mu}{n\to m,-x}dx=f(s)\left(\cos\left(\frac{2\pi m(1-s)}{\omega}\right)-\cos\left(\frac{2\pi n(1-s)}{\omega}\right)\right)$$

公式１を使ってひたすら計算するだけなので証明は省略します。
高階Airy関数の挙動はよくわからないので、$s$の範囲も場合によって考えなければいけませんね。
$s\to1$とすると次を得ます。

定理11

$n,m:left$について次が成り立つ。
$$\int_0^\infty \Aimu{\mu}{n,x}dx=1-\frac{2n}{\omega}$$
$$\int_0^\infty \Bimu{\mu}{n\to m,x}dx=0$$
また、$n,m:right$について次が成り立つ。
$$\int_0^\infty \Aimu{\mu}{n,-x}dx=\frac{2n}{\omega}$$
$$\int_0^\infty \Bimu{\mu}{n\to m,-x}dx=0$$

こんな性質も成り立ちます。

Airy関数の直交性

$$\int_{-\infty}^\infty\Ai{x+s}\Ai{x+s'}dx=\delta(s-s')$$

高階Airy関数の直交性

$\omega$が奇数のとき、次が成り立つ：
$$\int_{-\infty}^\infty\Aimu{\mu}{x+s}\Aimu{\mu}{x+s'}dx=\delta(s-s')$$
また、$\omega\equiv0$のとき、次が成り立つ：
$$\int_{-\infty}^\infty\Aimu{\mu}{x+s}\Aimu{\mu}{x+s'}dx=\frac{1}{2^{1/\omega}}\Aimu{\mu}{\frac{s-s'}{2^{1/\omega}}}$$

デルタ関数でごり押し

$\omega$が奇数なら、
$$\begin{align*}\int_{-\infty}^{\infty}\mathrm{Ai}^\mu(x+s)\mathrm{Ai}^\mu(x+s')dx &=\frac{1}{(2\pi i)^2} \int_{-\infty}^{\infty}\int_{-i\infty}^{i\infty}e^{-t^\omega/\omega+t(x+s)}dt\int_{-i\infty}^{i\infty}e^{-{t'}^\omega/\omega+t'(x+s')}dt'dx\\ &=\frac{1}{(2\pi)^2} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{it^\omega/\omega+i{t'}^\omega/\omega+its+it's'}\int_{-\infty}^{\infty}e^{ix(t+t')}dxdtdt'\\ &=\frac{1}{2\pi} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{it^\omega/\omega+i{t'}^\omega/\omega+its+it's'}\delta(t+t')dtdt'\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{it^\omega/\omega+i(-t)^\omega/\omega+its-its'}dt\\ &=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{it(s-s')}dt\\ &=\delta(s-s') \end{align*}$$
となる。$\omega\equiv0$なら四行目の式で$t^\omega$が打ち消されず、$\Aimu{\mu}{s}$の定義に帰着されますね。

これによって全く使いどころがわからない積分変換が定義でき、おなじみの性質が成り立ちます。

定理12

$\omega$が奇数の時、高階Airy変換を次のように定義する。
$$\mathcal{A}^\mu_x[f(x)](s)=\int_{-\infty}^\infty f(x)\mathrm{Ai}^\mu(x+s)dx$$
逆変換は自分自身になり、次の性質が成り立つ：
プランシュレルの定理
$$\int_{-\infty}^\infty f(x)g(x)dx=\int_{-\infty}^\infty \mathcal{A}^\mu_x[f(x)](s)\mathcal{A}^\mu_x[g(x)](s)ds$$
パーセバルの定理
$$\int_{-\infty}^\infty \abs{f(x)}^2dx=\int_{-\infty}^\infty \abs{\mathcal{A}^\mu_x[f(x)](s)}^2ds$$
積分で不変（定数が固有関数なのでプランシュレルの定理において$g=1$とする）
$$\int_{-\infty}^\infty f(x)dx=\int_{-\infty}^\infty \mathcal{A}^\mu_x[f(x)](s)ds$$
微分との順序交換
$$\frac{d^\mu}{ds^\mu}\mathcal{A}^\mu_x[f(x)](s)=\mathcal{A}^\mu_x\left[\frac{d^\mu}{dx^\mu}f(x)\right](s)=\mathcal{A}^\mu_x[xf(x)](s)+s\mathcal{A}^\mu_x[f(x)](s)$$

これで主要な積分が分かりました。ほかにもいくつか性質を見て高階Airy関数について終わります。

細々とした性質たち

$\omega\equiv0$のとき、$2\Aimu{\mu}{is}=\Bimu{\mu}{s}+\Bimu{\mu}{-s}$

$\omega\equiv2$のとき、$\Bimu{\mu}{\omega/2\to0,is}$は$\Ombar{\mu}{1}$の有界な解。

$C_n$と$C_m$が虚軸に関して互いに線対称なとき、$\Aimu{\mu}{n,s}=\Aimu{\mu}{m,-s}$

$C_n-C_m$と$C_{n'}-C_{m'}$が虚軸に関して線対称なとき、$\Bimu{\mu}{n\to m,s}=-\Bimu{\mu}{n'\to m',-s}$

Wronskian

$\omega\in2\mathbb{N}$のとき、実軸上もっともよく振舞う基本解のWronskianは$\sqrt{2}/\pi^{(\omega-1)/2}$となる。
$\omega\in2\mathbb{N}+1$のとき、実軸上もっともよく振舞う基本解のWronskianは$1/\pi^{\omega-2}$となる。

高階Scorer関数

非斉次なAiryの微分方程式：
$$D^2y=xy+\frac1\pi$$
の特殊解として通常、Scorer関数を次のように定義します。
$$\mathrm{Hi}(s)=\frac1\pi\int_0^\infty e^{-x^3/3+sx}dx\;,\;\;\mathrm{Gi}(s)=\frac1\pi\int_0^\infty \sin\left(\frac{x^3}{3}+sx\right)dx $$
$\mathrm{Hi}(s)+\mathrm{Gi}(s)=\Bi{s} $となるため、$\mathrm{Hi}(s)$と$-\mathrm{Gi}(s)$のどちらを特殊解として選んでも問題ないです。

この関数の類似を高階Airy関数に定義していきましょう。先ほどの図をもう一度見てみます。
経路の取り方

$$D^\mu y=xy+\frac1\pi$$の特殊解として、次の関数を定義します

高階Scorer関数

$$\Gi{\mu}{n,s}=\frac{1}{2\pi}\int_{-C_n-\bar{C}_n}e^{-x^\omega/\omega+sx}dx$$
$$\Hi{\mu}{s}=-\Gi{\mu}{0,s} $$
$C_n$が虚軸に接するセクターに含まれるとき、$\Gi{\mu}{n,s}$を単に$\Gi{\mu}{s}$と記す。

-
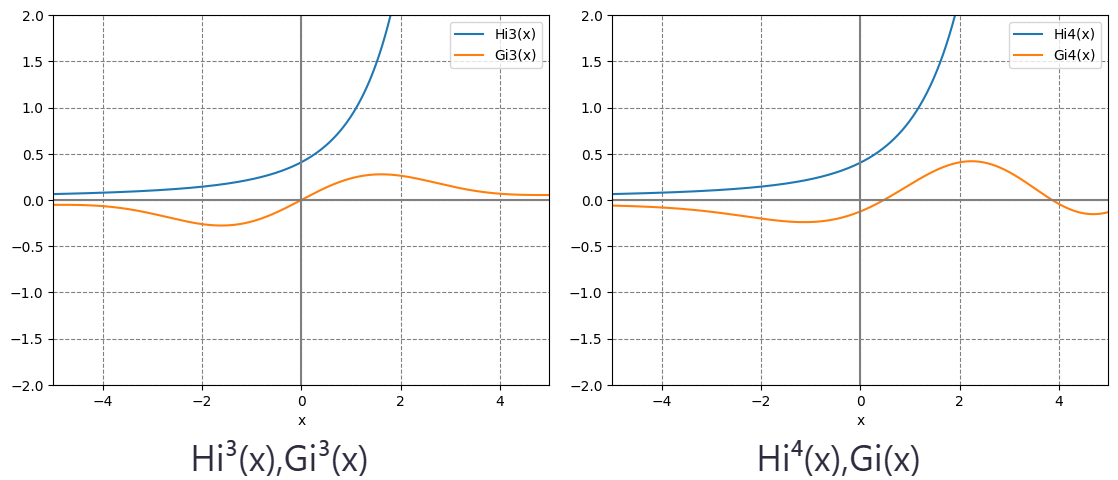実変数のScorer関数の関数のグラフ
$\Hi{\mu}{s},-\Gi{\mu}{n,s} $を特殊解として選ぶことができます。$-\Gi{\mu}{s}$は実軸上有界になので通常これを選びます。
Scorer関数に類似する性質が成り立ちます。

$\Bimu{\mu}{n\to m,s}$との関係

$$\Bimu{\mu}{n\to m,s}=\Gi{\mu}{n,s}-\Gi{\mu}{m,s}$$
$$\Bimu{\mu}{n,s}=\Gi{\mu}{n,s}+\Hi{\mu}{s}$$
$$\Bimu{\mu}{s}=\Gi{\mu}{s}+\Hi{\mu}{s}$$

経路の取り方から明らかですね。同じように、積分表示もできます。

積分表示

$$\Hi{\mu}{s}=\frac1\pi\int_0^\infty e^{-x^\omega/\omega+sx}dx$$
$$\Gi{\mu}{s}= \begin{eqnarray} \left\{ \begin{array}{l} \frac{1}{\pi }\int_{0}^{\infty} \sin\left(\frac{x^\omega}{\omega}+sx\right)dx\:\:(\omega\equiv3\mod4) \\ \frac{1}{\pi}\int_0^\infty e^{-x^\omega/\omega}\sin(sx)dx\:\:(\omega\equiv0\mod4)\\ \frac{1}{\pi }\int_{0}^{\infty} \sin\left(\frac{x^\omega}{\omega}-sx\right)dx\:\:(\omega\equiv1\mod4) \\ \end{array} \right. \end{eqnarray} $$

この関数についても様々な問題を考えられそうですが、次の類似をあげて終わりたいと思います。

Airy関数のHilbert変換

$$p.v.\int_{-\infty}^\infty\frac{\Ai{x}}{s-x}dx=\pi\mathrm{Gi}(s)$$

高階Airy関数のHilbert変換

$$p.v.\int_{-\infty}^\infty\frac{\Aimu{\mu}{x}}{s-x}dx=\pi\Gi{\mu}{s}$$