整式の方程式の複素数解を求める際に役に立つかもしれない考え方

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

以下の方程式の解を求めてください.
(1) $x^{4} + 1 = 0$
(2) $x^{4} - x^{2} + 1 = 0$

私たちが知っている公式は以下である.

$z^{n} = 1$ の解は $z = α_{k} = \cos \frac{2 k π}{n} + i \sin \frac{2 k π}{n}, (k = 0, . . ., n - 1)$ である.複素数平面上にこの点を描画すると以下のような図1となり,隣り合う点を結ぶと正n角形ができる.

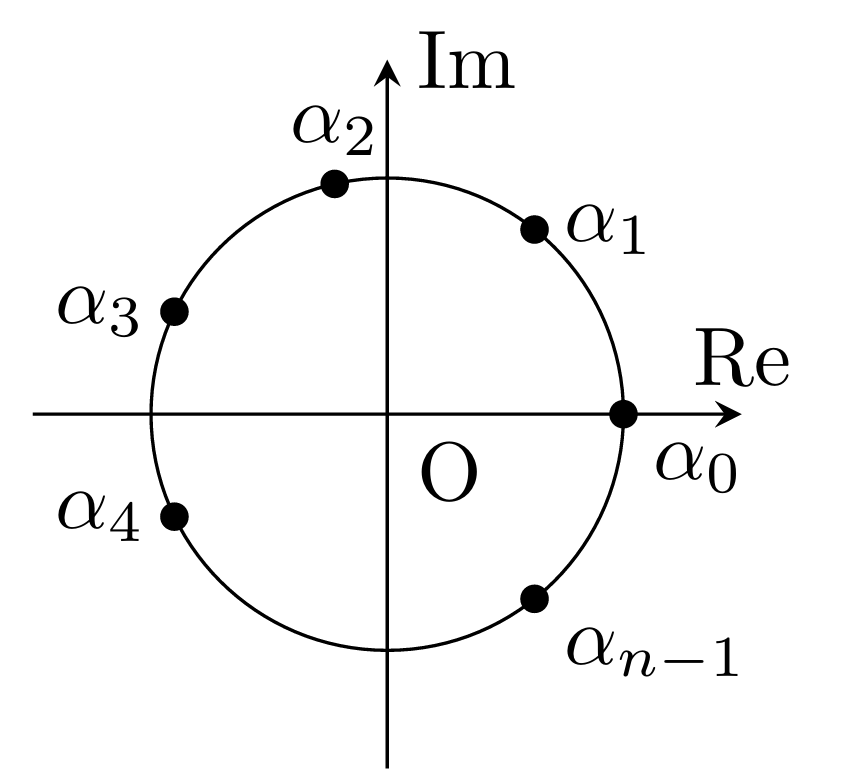
この公式をうまく使って上の例題を解いてあげようというのがこの記事の旨である.

(1)両辺に $x^{4} - 1$ をかけると $x^{8} - 1 = 0$ となる.公式を用いてあげると以下が解であることがわかる.

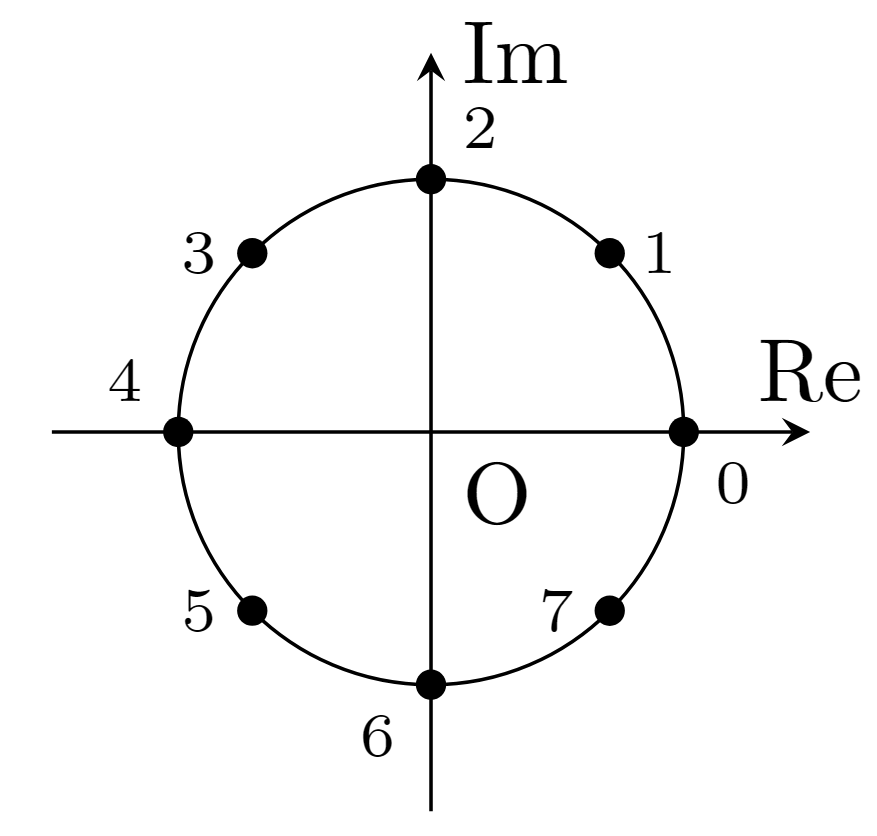
このうちかけた分( $x^{4} - 1 = 0$ )の解は $0, 2, 4, 6$ の点なので $1, 3, 5, 7$ がこの解である.

(2) $x^{4} - x^{2} + 1 = 0$ の両辺に $x^{2} + 1$ をかけると $x^{6} + 1 = 0$ が得られ,さらに $x^{6} - 1$ をかけると $x^{12} - 1 = 0$ が得られる.この解は以下の点である.

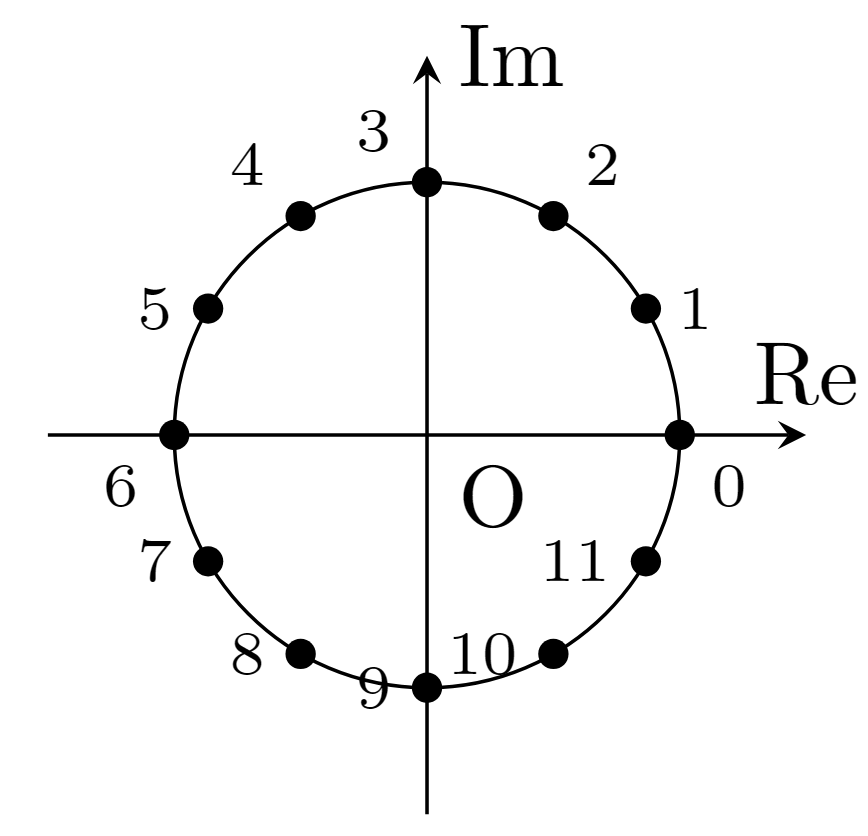
このうちかけた分( $x^{2} + 1 = 0$ , $x^{6} - 1 = 0$ )の解は $3, 6$ と $0, 2, 4, 6, 8, 10$ の点なので $1, 5, 7, 11$ がこの解である.

投稿日：3月11日

この記事を高評価した人

高評価したユーザはいません

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

197

数学。主に積分。

コメントはありません。

読み込み中