JMO2024本選4(幾何)
かばたんです. 初めまして. JMO2024本選がついこの前実施されました. 自分は４番で誤読をして本来なら解けていたはずのこの問題を落とし, 春合宿に行けるかかなり危うい状況です. 数学のモチベも特にないので, 戒めを含め解説でも書こうかなと思い立ちました.（実は初投稿です）
JMO2024本選4の解説
とりあえず解説を書いていこうと思います.
$AB< AC$を満たす鋭角三角形$ABC$があり, その外心を$O$, 三角形$ABC$の外接円の$A$を含まない方の弧$BC$の中点を$M$とする. 辺$AB$の$B$側の延長線上の点$D$が$BD=BM$を満たした. また, 辺$AC$（端点を除く）上の点$E$が$CE=CM$を満たした. 三角形$ABE$の外接円と三角形$ACD$の外接円が$A$出ない点$X$で交わっているとき, 線分$DE$の垂直二等分線は三角形$AOX$の外接円に接することを示せ.
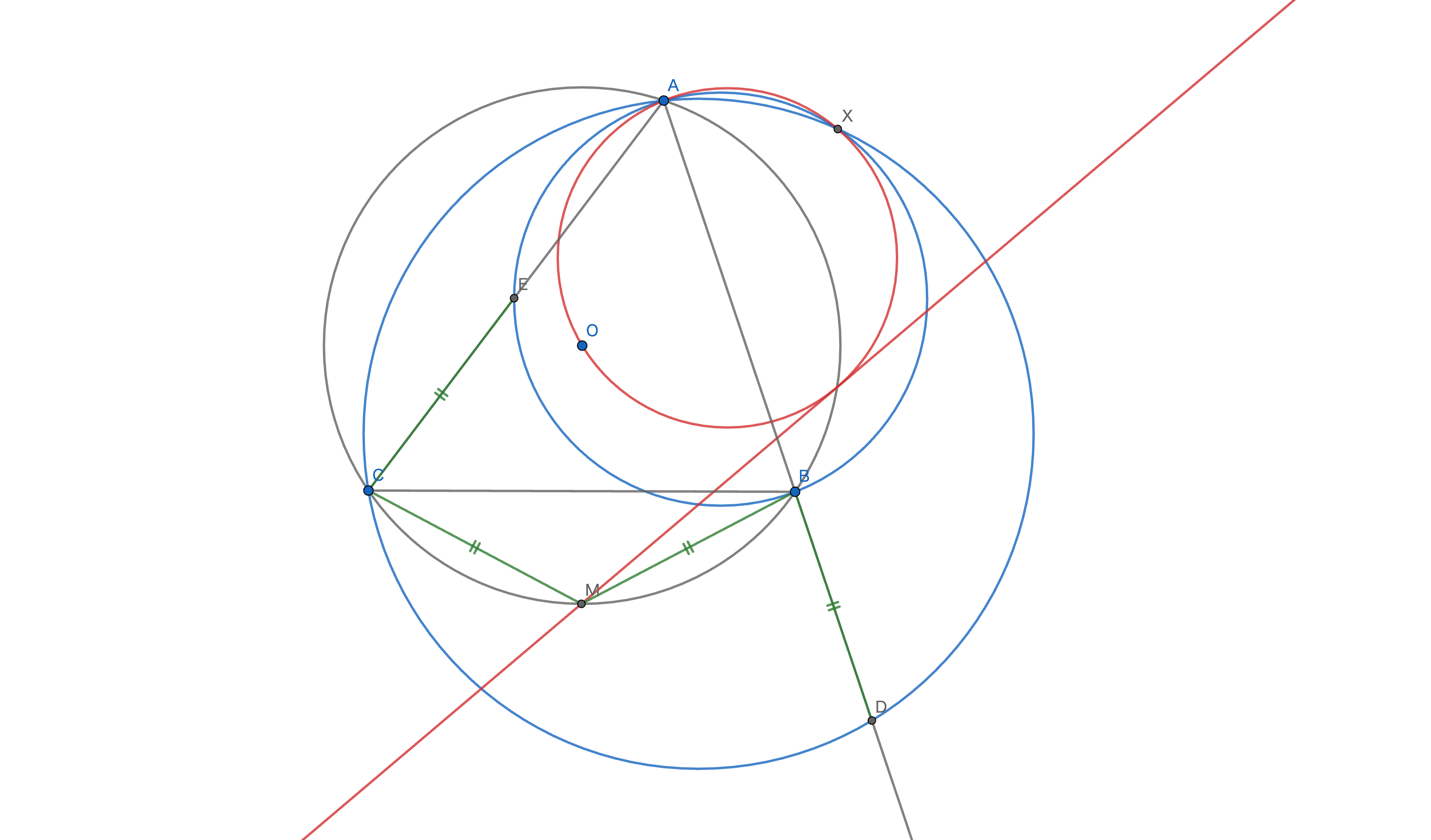問題の図
（Geogebraを使うと明らかに見えてしまいますが）コンパスで丁寧に作図すれば, 以下のような予想が立つはずです.
- $DE$の垂直二等分線は$M$を通る
- 問題となる接点は, 三角形$ABC$の外接円と三角形$AOX$の外接円の交点である
接点を$T$などと適当におけば, 以下の予想も立てられると思います（初見では気づきにくいと思いますが)
- 四角形$AXTO$は$AX\parallel OT$なる等脚台形である
まずはこれらを示すことを目標にしていきます. 実際一つ目の予想は比較的簡単に証明できます.
$A,D,E,M$は同一円周上にある. さらに$DE$の垂直二等分線は$M$を通る
内接四角形の定理より$\angle{MBD}=\angle{MCE}$であり, $BD=BM=CM=CE$だったので$\triangle{BMD}\equiv \triangle{CME}$となります. 従って$DM=ME$であり, $AM$が$\angle{BAC}$の二等分線だったことから$A,D,E,M$の共円がわかります. また$DE$の垂直二等分線が$M$を通ることもここからただちにわかります.
予想が一つ証明できました. 嬉しいですね. しかし二つ目以降はなかなかうまくいきません（簡単な方法があるのかもしれませんが）.
これは点$T$がまだかなり扱いにくいところから来ています. ということで, 点$T$をもう少し眺めてみます. すると, $T$が三角形$ADE$の外心になるのではないかと思えてきます（この点が$DE$の垂直二等分線上にあるので, 素直に外心を考えます). 実際に作図をして確認してみるといいと思います.
$T$は三角形$ADE$の外心である
![!FORMULA[46][37236][0]は三角形!FORMULA[47][35250694][0]の外心？](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F96QpejujytyZHBskccRp.png?alt=media)
$T$は三角形$ADE$の外心？
なんだか正しそうですね. ではこれを正当化するにはどうすればいいでしょうか？ 以下の二つを示せばいいわけです.
- 三角形$ADE$の外心を$O'$とすれば, $O'$は三角形$ABC$の外接円上にある.
- 四角形$AXO'O$は等脚台形をなす
これさえわかればangle-chasingで適当に終わりそうですね（実際終わります）. 一つ目の証明の方が素直なのでそっちから.
$O'$は三角形$ABC$の外接円上にある
同一法で示します. つまり, $OM$の垂直二等分線と$ABC$の外接円の交点$P$をとり, $O'=P$をいいます. $P$の定義より$AP=PM$なので$2\angle{ADM}=\angle{APM}$を言えばいいわけですが, これはかなり簡単にわかります（補題1が重要な役割を果たしています）.
$\angle{AOP}=\angle{MOP}=\angle{MBD}=\angle{ACB}$より$\triangle{OAP}=\triangle{OMP}=\triangle{BMD}$が従い示されました.
さて, ここまでは基本的な内容でできるわけですが, 最後の補題の証明は少し難しいです（僕も試験中この証明に苦労しました. 後述）. ここで$BD=CE$が生きてきます. かなり綺麗でめっちゃ好きです.
四角形$AXO'O$は等脚台形である
三角形$ABE,ACD$の外心を$O_1,O_2$とします. $AX$はこれらの外接円の根軸であり$O_1O_2\perp AX$となるので, 四角形$OO_1O'O_2$が菱形になることを言えばいいとわかります（これを言えば, $O_1O_2\perp OO'$より$AX\parallel OO'$であることと, $O_1O=O_1O'$ことより主張が従います. $O_1$は三角形$ABE$の外心だったので$O_1A=O_1X$が成り立つことに注意.）.
さて, $AB,AD,AC,AE$の垂直二等分線を$l_1,l_2,l_3,l_4$としましょう. 明らかに$l_1\parallel l_2$かつ$l_3\parallel l_4$なので$OO_1O'O_2$が平行四辺形になるとわかります. つまり$OO_1=OO_2$を示せば十分ですが, これは$l_1$と$l_2$の距離と$l_3$と$l_4$の距離が等しいことと同値です（詳細は省きます）. 一方, よく考えれば$l_1$と$l_2$の距離は$AB$の中点と$AD$の中点の距離なので, $\dfrac{1}{2}(AD-AB)=\dfrac{1}{2}BD$に等しいです. 同様に$l_3$と$l_4$の距離は$\dfrac{1}{2}CE$となるので$BD=CE$より主張が示されました.
綺麗ですね〜. 自分が試験中この証明を思いついたときには感動したんですけども（笑）. さっきも言いましたけどまるで死んでいたように思える$BD=CE$がめっちゃ効いてくるのが好きなポイントです.
さてあとは消化試合です. 接弦定理より$\angle{OAT}=\angle{OTM}$を示せばいいわけですが, $\angle{OAT}=\angle{OTA}=\angle{OTM}$よりこれは簡単に従います！よってこの問題を解くことができました.
誤読について
ここからはたぶん多くの受験者がやらかし, 僕も試験中にやってしまった誤読についてです. 問題文を載せたときに「辺」が強調されていたことから察していたと思いますが, 以下のような誤読をしてしまいました.
$AB< AC$を満たす鋭角三角形$ABC$があり, その外心を$O$, 三角形$ABC$の外接円の$A$を含まない方の弧$BC$の中点を$M$とする. 辺$AB$の$B$側の延長線上の点$D$が$BD=BM$を満たした. また, 辺$AC$の$C$側の延長線上の点$E$が$CE=CM$を満たした. 三角形$ABE$の外接円と三角形$ACD$の外接円が$A$出ない点$X$で交わっているとき, 線分$DE$の垂直二等分線は三角形$AOX$の外接円に接することを示せ.
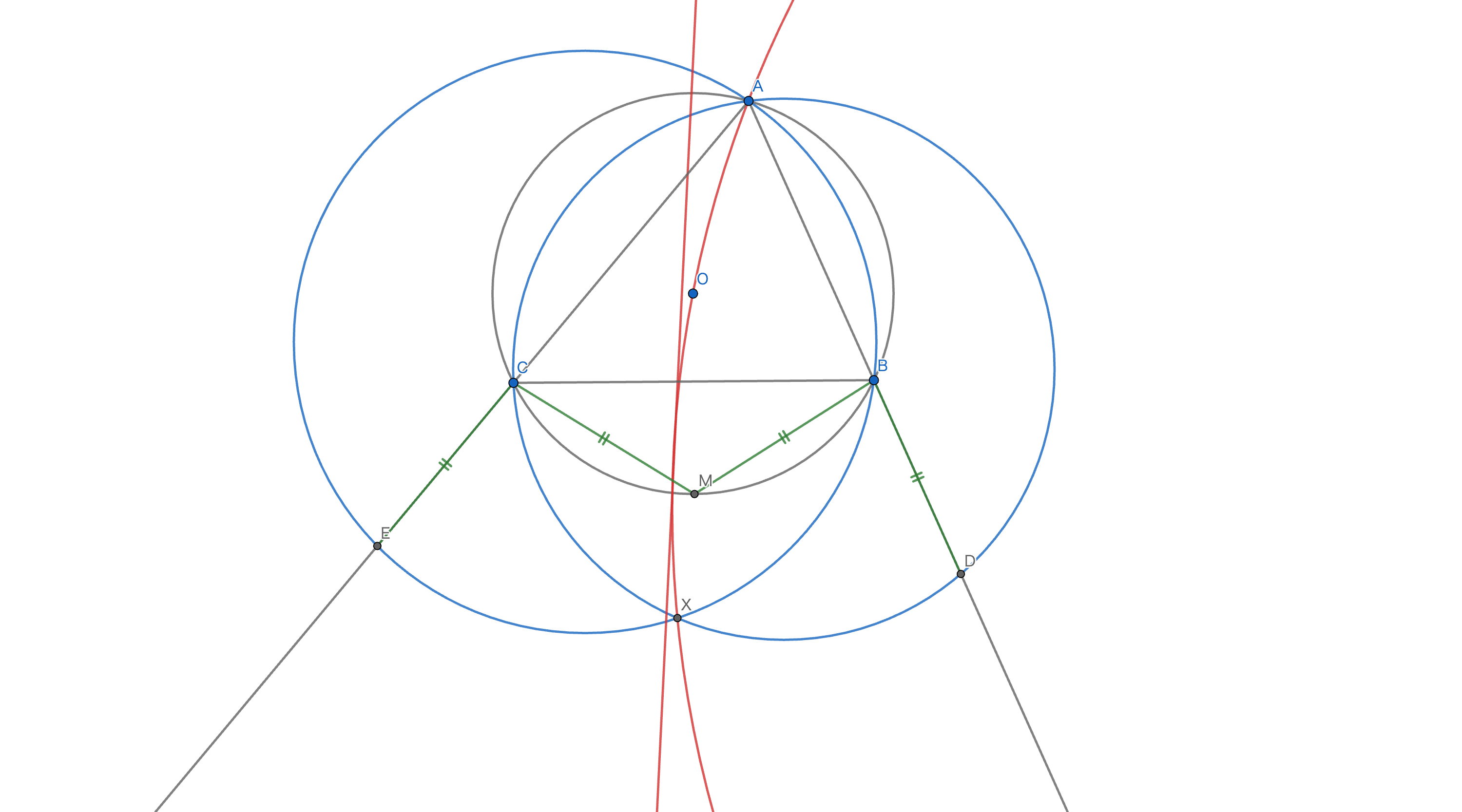これは接線です
図を見ればわかると思いますが, この誤読が頻発した原因はぱっと見主張が成立している点にあります. コンパス作図でこれを接していないと見抜ける人はいないでしょう. さらに$A,B,D$の位置関係と$A,C,E$の位置関係が対称である点, $A,M,X$が共線のように見え図形的性質も比較的良さそうに思える点がその誤読を後押ししています. 実際に$A,M,X$は共線であり, 三角形$XBD$と$XEC$は合同になっていました. また, 先ほどの解説でかなり重要であった四角形$AOO'X$も, なんと等脚台形になります（試験中の僕もこのことに気がつきました）. せっかくなのでその辺に触れていこうと思います.
$A,M,X$は共線である
実は問題を解く上ではそんなに関係ないですが, せっかくなので証明します. まず内接四角形の定理より$\angle{XBD}=\angle{XCE},\angle{XDB}=\angle{XCE}$であり, $BD=CE$だったので$\triangle{XBD}\equiv\triangle{XEC}$が成り立ちます. 従って$BX=EX$となるので$AX$は$\angle{BAC}$の二等分線になりますが, $AM$もそうだったのでこれらは一致します. よって示されました.
$O'$を三角形$ADE$の外心とする. 四角形$AOO'X$は等脚台形である
先ほどの解説での補題3と全く同じ証明で示せます.
ここまでを導いた僕は, あとは適当にangle-chasingをすれば終わるだろうと思っていました. しかし全然解けない！そりゃそうです. そもそも主張が間違っているので. そうこうしているうちに時間がなくなり, 上の内容を解答用紙に書いたところで試験が終わりました. 終了直後は誤読に気づいていないので, まあ半分はもらえるだろうと考えていたのを覚えています.（その後たけまさとHi_mathと話しているときに誤読に気がついて絶望しました）
終わりに
誤読には気をつけましょう. この誤読がなければ4番を普通に倒せて春には余裕を持って行けていたと思うのでかなり悔しいです. （図が間違えているので厳しいと思いますが）なんとか部分点が入って春合宿に奇跡的に行けることを期待するばかりです.
この記事を高評価した人
この記事に送られたバッジ
投稿者
