直交する２直線と４円からなる共円・共線・双心四角形の性質について

はじめに

　平面上の異なる４円が以下の図のような関係になっている場合について、いくつか性質を発見したので紹介します。
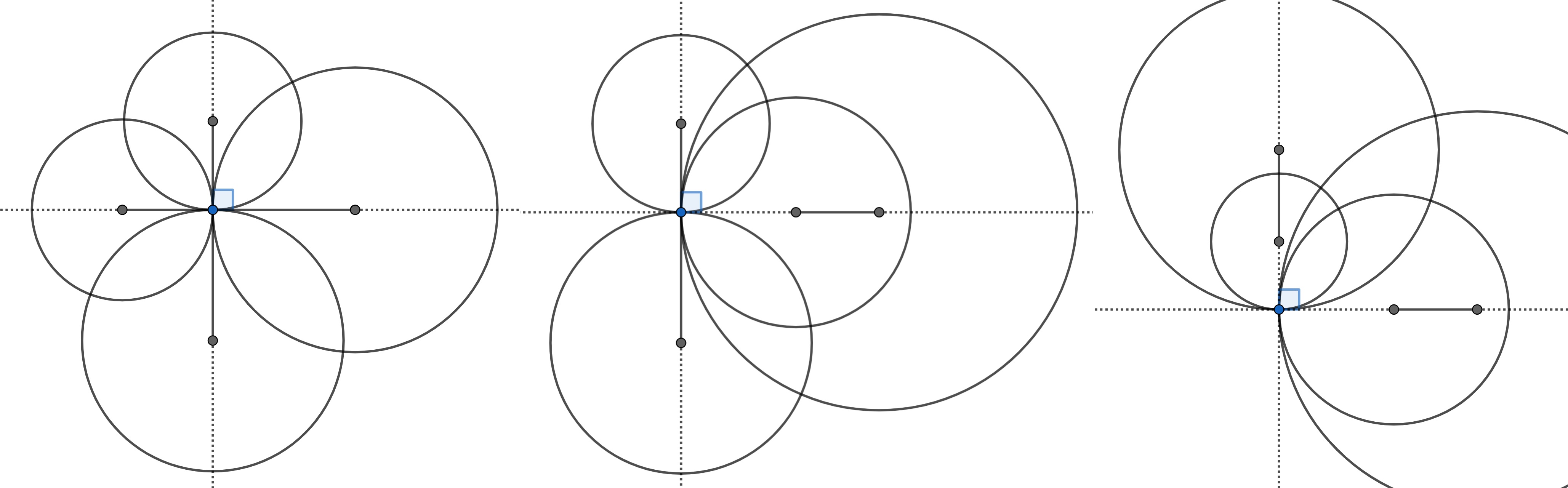直交する２直線と４円
　
＊注意
　既に知られている性質もあるかもしれません。予めご了承ください。
また、これより良い証明方法がおそらくあると思います。思いついた方がいましたら、教えていただけると助かります。
　
$\ $

性質

　
　言葉だけだと伝わりにくいと思うので、GeoGebraにて図を作成しました。（画像をクリックすると、実際にパラメーターを動かすことができるページに移動します。）
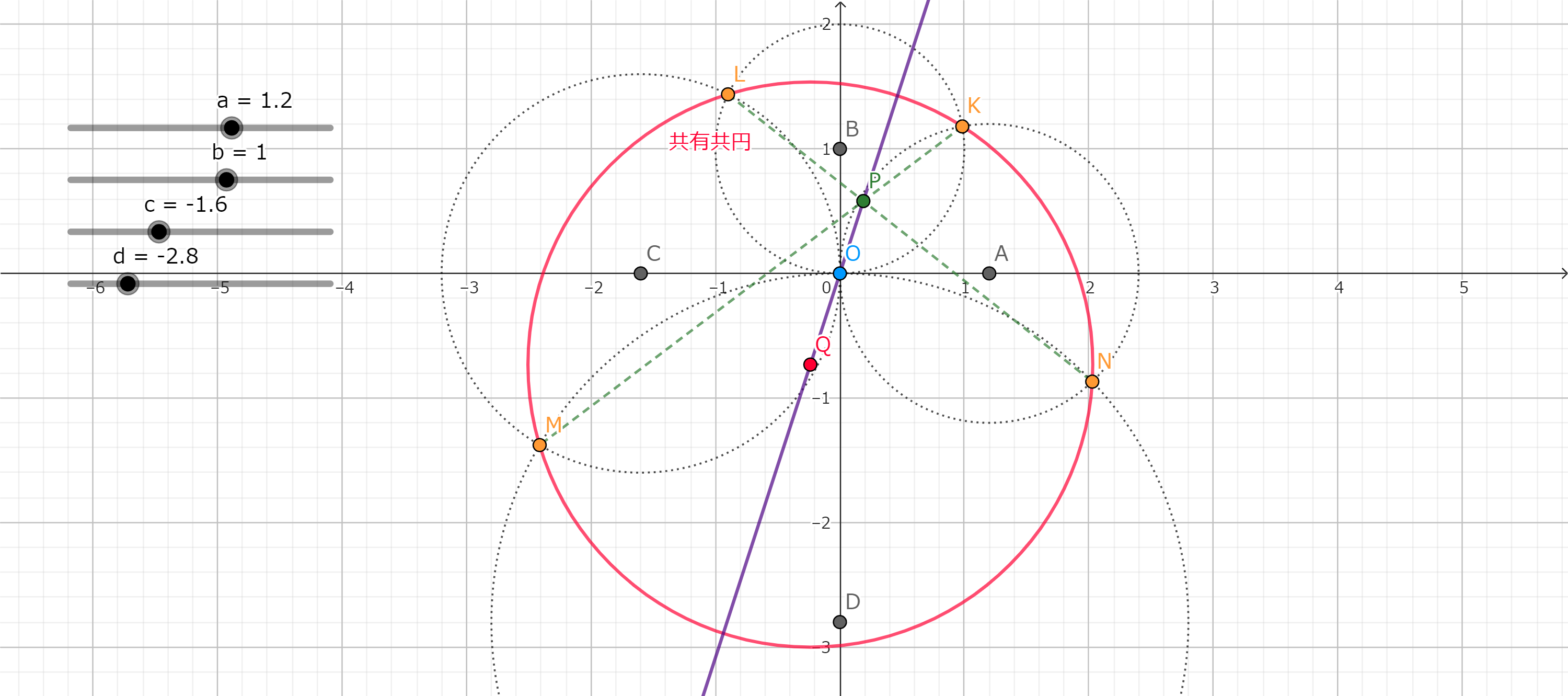GeoGebra
　
　この他にも、「線分 OA,OC の長さがそれぞれ等しくないとき、３直線 AC,KL,MN が一点で交わる」など様々な性質がありますが、そこまで書くと長くなってしまうので、今回は比較的有用であると判断した上記の性質について証明していきます。（いつか他の性質についても証明したいです。）
　
$\ $

性質の証明

準備

　直線 AC と直線 BD が点 O で直交していることから、$xy$ 平面で考えると良さそうです。0でない任意の実数 $a,b,c,d$ ($a≠c, \ b≠d$) を用いて、点 O を $(0,0)$ 、点 A を $(a,0)$ 、点 B を $(0,b)$ 、点 C を $(c,0)$ 、点 D を $(0,d)$ とそれぞれおきます。このとき、４円それぞれの方程式は以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} C_{\mathrm{A}}:(x-a)^2+y^2=a^2 \\ C_{\mathrm{B}}:x^2+(y-b)^2=b^2 \\ C_{\mathrm{C}}:(x-c)^2+y^2=c^2 \\ C_{\mathrm{D}}:x^2+(y-d)^2=d^2 \\ \end{array} \end{eqnarray} $$
　
　この方程式同士を連立することで、点 K が $(\frac{2ab^2}{a^2+b^2},\frac{2a^2b}{a^2+b^2})$ 、点 L が $(\frac{2b^2c}{b^2+c^2},\frac{2bc^2}{b^2+c^2})$ 、点 M が $(\frac{2cd^2}{c^2+d^2},\frac{2c^2d}{c^2+d^2})$ 、点 N が $(\frac{2d^2a}{d^2+a^2},\frac{2da^2}{d^2+a^2})$ であることが分かります。

$\ $

〔Ⅰ〕の証明

　まず、直線 AC と直線 BD 、直線 AB と直線 CD がそれぞれ直交していることから、点 A が三角形 BCD の垂心であると分かります。したがって垂心の性質より、直線 DA と直線 BC は直交します。
　
　次に点 E,D の座標をそれぞれ求めましょう。直線 AB,BC,CD,DA の方程式はそれぞれ以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{AB}}:y=-\frac{b}{a}x+b \\ {\mathrm{BC}}:y=-\frac{b}{c}x+b \\ {\mathrm{CD}}:y=-\frac{d}{c}x+d \\ {\mathrm{DA}}:y=-\frac{d}{a}x+d \\ \end{array} \end{eqnarray} $$
　
直線 AB と直線 CD が直交するため、垂直条件より
$$ \left(-\frac{b}{a}\right)\left(-\frac{d}{c}\right)=-1 \Longleftrightarrow ac=-bd$$
が成り立ちます。さらに変形すると
$$ abcd=-b^2d^2<0$$
と表せるため、それぞれ以下のように 0 でないことを示せます。
$$ \begin{eqnarray} \begin{array}{l} abcd-b^2c^2<0 \Longrightarrow da-bc≠0 \\ abcd-c^2d^2<0 \Longrightarrow ab-cd≠0 \end{array} \end{eqnarray} $$
　
　これらを利用して方程式同士を連立すると、点 E が $(-\frac{ac(b-d)}{da-bc},\frac{bd(a-c)}{da-bc})$ 、点 F が $(\frac{ac(b-d)}{ab-cd},\frac{bd(a-c)}{ab-cd})$ であると分かります。また、直線 EF の方程式を求めると以下のようになります。
$$ {\mathrm{EF}}:(a+c)x-(b+d)y=2ac$$
点 K,L,M,N の座標を直線 EF の方程式に代入してみると、$ac=-bd$ を用いることでいずれの等式も成立することが分かります。
　
　以上より、６点 E,F,K,L,M,N は同一直線上にあることが示されました。
　
　$\ $

〔Ⅱ〕１．の証明

　３点 L,M,N を通る円 $C_\mathrm{Q}$ について考えましょう。まず実数 $l,m,n$ を用いて円 $C_\mathrm{Q}$ の方程式を以下のように定義します。
$$ C_\mathrm{Q}:x^2+y^2+lx+my+n=0$$
この方程式に３点 L,M,N の座標をそれぞれ代入して整理すると、
$$ \begin{eqnarray} \left\{ \begin{array}{l} 4b^2c^2+2b^2cl+2bc^2m+(b^2+c^2)n=0 \\ 4c^2d^2+2cd^2l+2c^2dm+(c^2+d^2)n=0 \\ 4d^2a^2+2d^2al+2da^2m+(d^2+a^2)n=0 \end{array} \right. \end{eqnarray} $$
と表せます。それぞれ連立して解くと以下のように表せます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} l=-\frac{2bd(a+c)}{ac+bd} \\ m=-\frac{2ac(b+d)}{ac+bd} \\ n=\frac{4abcd}{ac+bd} \end{array} \right. \end{eqnarray} $$
（直線 AB と直線 CD が直交しないため、〔Ⅰ〕より $ac+bd≠0$ ）
　
　よって、円 $C_\mathrm{Q}$ の方程式は以下のように表せます。
$$ C_\mathrm{Q}:x^2+y^2-\frac{2bd(a+c)}{ac+bd}x-\frac{2ac(b+d)}{ac+bd}y+\frac{4abcd}{ac+bd}=0$$
この方程式に点 K の座標を代入すると等式が成立するため、４点 K,L,M,N が同一円周上にあると分かります。
　
　後の証明で使うため、中心点 Q の座標を求めます。円 $C_\mathrm{Q}$ の方程式を変形すると、以下のように表せます。
$$ C_\mathrm{Q}:\left( x-\frac{bd(a+c)}{ac+bd}\right) ^2+\left(y-\frac{ac(b+d)}{ac+bd}\right)^2=\frac{b^2d^2(a-c)^2+a^2c^2(b-d)^2}{(ac+bd)^2}$$
したがって、点 Q の座標は $(\frac{bd(a+c)}{ac+bd},\frac{ac(b+d)}{ac+bd})$ であると分かります。
　
　
　続いて、４点 K,L,M,N がこの順であることを場合分けして示します。
　$\ $

$ \angle \mathrm{KLM}=\angle \mathrm{KNM}= 90^{\circ} $ であるとき

　線分 KM は直径であるため、点 Q が２点 K,M の中点であることが分かります。したがって、以下の２つの等式が成り立ちます。
$$ \begin{eqnarray} \begin{array}{l} \frac{1}{2} \left( \frac{2ab^2}{a^2+b^2}+\frac{2cd^2}{c^2+d^2} \right) =\frac{bd(a+c)}{ac+bd} \\ \frac{1}{2} \left( \frac{2a^2b}{a^2+b^2}+\frac{2c^2d}{c^2+d^2} \right) =\frac{ac(b+d)}{ac+bd} \end{array} \end{eqnarray} $$
この２つの等式をそれぞれ整理すると以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} (da-bc)\left( a^2b(c^2+d^2)-c^2d(a^2+b^2) \right)=0 \\ (da-bc)\left( ab^2(c^2+d^2)-cd^2(a^2+b^2) \right)=0 \end{array} \end{eqnarray} $$
　
この２つの等式を満たすためには、
$da-bc=0$ であるか、
$a^2b(c^2+d^2)-c^2d(a^2+b^2)=0$ かつ $ab^2(c^2+d^2)-cd^2(a^2+b^2)=0$ であるか
のどちらかの条件を満たす必要があります。
　
後者の条件が成り立つことは、
$$ \left( a^2b(c^2+d^2)-c^2d(a^2+b^2) \right)^2+\left( ab^2(c^2+d^2)-cd^2(a^2+b^2) \right)^2 $$
が 0 であることと同値です。この式を整理すると以下のように表せます。
$$ (a^2+b^2)(c^2+d^2)\left( a^2c^2(b-d)^2+b^2d^2(a-c)^2 \right)$$
この式が 0 にならないことは明らかなので、$a^2b(c^2+d^2)-c^2d(a^2+b^2)=0$ かつ $ab^2(c^2+d^2)-cd^2(a^2+b^2)=0$ を満たす実数 $a,b,c,d$ は存在しないことが分かります。
　
　以上より、$ \angle \mathrm{KLM}=\angle \mathrm{KNM}= 90^{\circ} $ であることと、$da-bc=0$ であることが同値であると分かりました。
　
（証明上では４点 K,L,M,N が同一円周上にある前提でしたが、〔Ⅰ〕と〔Ⅱ〕１．の証明より、４点 K,L,M,N が同一円周上にないときは４点 K,L,M,N は同一直線上にあり、$da-bc≠0$ であることが示されているため、同値関係が成り立ちます。）
　
　$da-bc=0$ であることを用いると、直線 OQ の式は以下のように表せます。
$$ \mathrm{OQ}:y=\frac{a}{b}x$$
この方程式に２点 K,M の座標を代入すると、どちらも方程式を満たします。したがって、４点 K,M,O,Q は同一直線上にあることが分かります。
　
　ここで、共有共円の円周のうち $y>\frac{a}{b}x$ を満たす弧を $A_1$ 、$y<\frac{a}{b}x$ を満たす弧を $A_2$ とすると、２点 L,N はどちらかの弧上にあることが分かります。
　
　続いて直線 OQ と平行な直線を、任意の実数 $k$ を用いて以下のように定義します。
$$ y=\frac{a}{b}x+k $$
このとき、この直線は $k>0$ であるとき $A_1$ と、$k<0$ であるとき $A_2$ とそれぞれ共有点を持つことが分かります。この直線が２点 L,N をそれぞれ通るときの $k$ の値は、それぞれ以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} \mathrm{L}:k=-\frac{2bc(a-c)}{b^2+c^2} \\ \mathrm{N}:k=\frac{2bc(a-c)}{d^2+a^2} \end{array} \end{eqnarray} $$
$2bc(a-c)≠0$ であるため、$k$ の符号はそれぞれ異なっています。したがって、２点 L,N のうちどちらか１点は $A_1$ にあり、もう一方の１点は $A_2$ にあることが分かります。
　
　よって、直線 KM に対して２点 L,N が互いに異なる側にあるため、４点 K,L,M,N がこの順に同一円周上にあることが示せます。
　$\ $

$ \angle \mathrm{KLM}=\angle \mathrm{KNM}= 90^{\circ} $ でないとき

　$ \angle \mathrm{KLM}+\angle \mathrm{KNM}= 180^{\circ} $ であるとき、４点 K,L,M,N がこの順で同一円周上にあることが円周角の定理より分かります。また $ \angle \mathrm{KLM}+\angle \mathrm{KNM}≠ 180^{\circ} $ であるとき、直線 KM に対して２点 L,N は同じ側にあることになるため、４点 K,L,M,N がこの順ではなく、$ \angle \mathrm{KLM}=\angle \mathrm{KNM}$ が成り立つことが円周角の定理より分かります。
　
　ここで内積 $ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}} $ , $ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}} $ の符号について考えると、$ \angle \mathrm{KLM}$, $\angle \mathrm{KNM}$ がそれぞれ鋭角であるときは正、それぞれ鈍角であるときは負になります。
　
　よって４点 K,L,M,N が同一円周上にあり、$ \angle \mathrm{KLM}=\angle \mathrm{KNM}= 90^{\circ} $ でないとき、$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}} $ , $ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}} $ の符号が互いに異なるならば $ \angle \mathrm{KLM}+\angle \mathrm{KNM}= 180^{\circ} $ であり、$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}} $ , $ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}} $ の符号が互いに同じであるならば $ \angle \mathrm{KLM}=\angle \mathrm{KNM}$ であることが分かります。では、それぞれの内積を求めていきましょう。
　
　$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}} $ の値は以下のように表せます。
$$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}}=\left( \frac{2ab^2}{a^2+b^2}-\frac{2b^2c}{b^2+c^2} \right)\left( \frac{2cd^2}{c^2+d^2}-\frac{2b^2c}{b^2+c^2} \right)+\left( \frac{2a^2b}{a^2+b^2}-\frac{2bc^2}{b^2+c^2} \right)\left( \frac{2c^2d}{c^2+d^2}-\frac{2bc^2}{b^2+c^2} \right)$$
整理すると以下のように表せます。
$$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}}=\frac{4b^2c^2(a-c)(b-d)(da-bc)}{(a^2+b^2)(b^2+c^2)(c^2+d^2)}$$
$ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}} $ の値も同様に整理すると以下のように表せます。
$$ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}}=-\frac{4a^2d^2(a-c)(b-d)(da-bc)}{(c^2+d^2)(d^2+a^2)(a^2+b^2)}$$
$ \angle \mathrm{KLM}=\angle \mathrm{KNM}= 90^{\circ} $ でないことから、$ \overrightarrow{\mathrm{LK}} \cdot \overrightarrow{\mathrm{LM}} $ , $ \overrightarrow{\mathrm{NK}} \cdot \overrightarrow{\mathrm{NM}} $ の符号は互いに異なることが分かります。
　
　したがって、$ \angle \mathrm{KLM}+\angle \mathrm{KNM}= 180^{\circ} $ であり、４点 K,L,M,N がこの順に同一円周上にあることが示せます。
　
　
　以上より、どちらの場合においても４点 K,L,M,N がこの順に同一円周上にあることが示されました。
　
　$\ $

〔Ⅱ〕２．の証明

　点 O,Q の座標はすでに分かっているので、点 P の座標を求めたいです。まず、直線 KM,LN の方程式はそれぞれ以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{KM}}:(cd^2a^2+b^2cd^2-ab^2c^2-d^2ab^2)y-(c^2da^2+b^2c^2d-a^2bc^2-d^2a^2b)x=2abcd(da-bc) \\ {\mathrm{LN}}:(c^2d^2a+d^2ab^2-a^2b^2c-b^2cd^2)y-(c^2da^2+da^2b^2-a^2bc^2-bc^2d^2)x=2abcd(cd-ab) \end{array} \end{eqnarray} $$
これらを連立することで点 P の座標を求められるのですが、計算が複雑になってしまいます。
　
　今回最終的に証明したいことは、直線 OQ が点 P を通ることです。言い換えると、３直線 KM,LN,OQ が一点 P で交わることを示せば良さそうです。直線 OQ は

$a+c=0$ のとき、
$$ \mathrm{OQ}:x=0$$
$a+c≠0$ のとき、
$$ \mathrm{OQ}:y=\frac{ac(b+d)}{bd(a+c)}x$$
とそれぞれ表せるので、直線 OQ と直線 KM の交点 P'、直線 OQ と直線 LN の交点 P'' のそれぞれの座標は、点 P より求めやすそうです。場合分けをして、２点 P',P'' の座標について考えてみましょう。
　$\ $

$a+c=0$ のとき

　直線 KM の方程式の $x$ に 0 を代入して整理すると、以下のように表せます。
$$ (cd^2a^2+b^2cd^2-ab^2c^2-d^2ab^2)y=2abcd(da-bc)$$
$a+c=0$ より、さらに整理すると以下のように表せます。
$$ a(d^2a^2+2b^2d^2+a^2b^2)y=2a^3bd(b+d)$$
$a(d^2a^2+2b^2d^2+a^2b^2)≠0$ であることは明らかなので、$y$ について解くと以下のように表せます。
$$ y=\frac{2a^2bd(b+d)}{d^2a^2+2b^2d^2+a^2b^2}$$
したがって、点 P' の座標は $(0,\frac{2a^2bd(b+d)}{d^2a^2+2b^2d^2+a^2b^2})$ であると分かります。
　
　点 P'' についても同様に座標を求めると、$(0,\frac{2a^2bd(b+d)}{d^2a^2+2b^2d^2+a^2b^2})$ であると分かります。２点 P',P'' が同一の座標であるので、３直線 KM,LN,OQ が点 P $(0,\frac{2a^2bd(b+d)}{d^2a^2+2b^2d^2+a^2b^2})$ で交わることが分かります。
　
　よって $a+c=0$ のとき、３点 O,P,Q は同一直線上にあることが示せました。
　$\ $

$a+c≠0$ のとき

　直線 KM の方程式の $y$ に、直線 OQ の方程式を代入して整理すると、以下のように表せます。
$$ \left((cd^2a^2+b^2cd^2-ab^2c^2-d^2ab^2)ac(b+d)-(c^2da^2+b^2c^2d-a^2bc^2-d^2a^2b)bd(a+c) \right)x=2ab^2cd^2(da-bc)(a+c)$$
少し計算が大変ですが、左辺をさらに整理すると以下のように表せます。
$$ (a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2)(da-bc) x=2ab^2cd^2(da-bc)(a+c)$$
$a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2≠0 $ であることは明らかですが、$da-bc$ については 0 になることもあるため、$x$ について解くためには場合分けが必要です。
　$\ $

$da-bc=0$ のとき

　〔Ⅱ〕１．より、４点 K,M,O,Q が同一直線上にあるため、直線 KM と直線 LN の交点 P が直線 OQ 上にあるのは明らかです。（４点 K,L,M,N がこの順に同一円周上にあるため、線分 KM と線分 LN は交点を持つ。）
　$\ $

$da-bc≠0$ のとき

　点 P' の座標は $\left( \frac{2ab^2cd^2(a+c)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2},\ \frac{2a^2bc^2d(b+d)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2} \right)$ と表せます。同様にして点 P'' の座標も求めると、$\left( \frac{2ab^2cd^2(a+c)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2},\ \frac{2a^2bc^2d(b+d)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2} \right)$ と表せることが分かります。よって２点 P',P'' が同一の座標であるので、３直線 KM,LN,OQ が点 P $\left( \frac{2ab^2cd^2(a+c)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2},\ \frac{2a^2bc^2d(b+d)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2} \right)$ で交わることが分かります。
　
　
　よって $a+c≠0$ のときも、３点 O,P,Q は同一直線上にあることが示されたため、いずれの場合においても３点 O,P,Q は同一直線上にあることが示されました。
　
　今回は示しませんでしたが、$ac+bd≠0$ であるとき、いずれの場合も点 P の座標は $\left( \frac{2ab^2cd^2(a+c)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2},\ \frac{2a^2bc^2d(b+d)}{a^2b^2c^2+b^2c^2d^2+c^2d^2a^2+d^2a^2b^2} \right)$ と表せます。
　
　$\ $

〔Ⅲ〕１．の証明

　線分 AC と線分 BD が点 O で交わることから、$a,c$ の符号、$b,d$ の符号はどちらもそれぞれ互いに異なっています。

　４点 A,B,C,D が同一円周上にあるとき、その円を $C'$ とします。このとき、方べきの定理より以下が成り立ちます。
$$ \mathrm{OA} \cdot \mathrm{OC} = \mathrm{OB} \cdot \mathrm{OD} \Longleftrightarrow \left| a \right| \left| c \right| = \left| b \right| \left| d \right| \Longleftrightarrow \left| ac \right| = \left| bd \right| $$
また、 $ac<0$, $bd<0$ であるため、$ac=bd$ が成り立ちます。
　
　よって $ac+bd≠0$ であるため、〔Ⅱ〕１．より４点 K,L,M,N がこの順に同一円周上にあることが分かります。
　
　続いて円 $C'$ の方程式を求めると、以下のように表せます。
$$ C':\left( x-\frac{a+c}{2} \right)^2+\left( y-\frac{b+d}{2} \right)^2=\frac{a^2+b^2+c^2+d^2}{4}$$
したがって円 $C'$ の中心 Q'' の座標は、$\left(\frac{a+c}{2}, \ \frac{b+d}{2} \right)$ だと分かります。
　
　次に〔Ⅱ〕１．より、４点 K,L,M,N を通る円 $C$ の中心 Q' の座標は、$\left(\frac{a+c}{2}, \ \frac{b+d}{2} \right)$ だと分かります。

　よって、２点 Q',Q'' が一致することが示されました。
　
　$\ $

〔Ⅲ〕２．の証明

　四角形 KLMN が双心四角形であることを示すために、以下の定理を用います。

今回はこの定理の証明を省略して用います。（証明が気になる方は、 ピトーの定理 - Wikipedia の脚注にある PDF(英語) がおそらくこの定理の証明に該当します。）
　
　四角形 KLMN の各辺の長さを求めると、それぞれ以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{KL}}:\frac{2\left| b \right|\left| a-c \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ {\mathrm{LM}}:\frac{2\left| c \right|\left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ {\mathrm{MN}}:\frac{2\left| d \right|\left| a-c \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ {\mathrm{NK}}:\frac{2\left| a \right|\left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \end{array} \end{eqnarray} $$
このとき、２組の対辺の長さの和はそれぞれ以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{KL}}+{\mathrm{MN}}=\frac{2\left( \left| b \right| + \left| d \right| \right)\left| a-c \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ {\mathrm{LM}}+{\mathrm{NK}}=\frac{2\left( \left| a \right| + \left| c \right| \right)\left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \end{array} \end{eqnarray} $$
　
　$-ac=\left| ac \right|$ であるため、以下の同値関係が成り立ちます。
$$ -ac=\left| ac \right| \Longleftrightarrow \left| a-c \right|^2=\left( \left| a \right| + \left| c \right| \right)^2 \Longleftrightarrow \left| a-c \right| = \left| a \right| + \left| c \right|$$
$ac=bd$ より、同様にして以下の等式が成り立ちます。
$$ \left| b-d \right| = \left| b \right| + \left| d \right|$$
　
　したがって、以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{KL}}+{\mathrm{MN}}=\frac{2\left| a-c \right| \left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ {\mathrm{LM}}+{\mathrm{NK}}=\frac{2\left| a-c \right| \left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \end{array} \end{eqnarray} $$
よって、四角形 KLMN は２組の対辺の長さの和が等しい凸な四角形であるため、四角形 KLMN は内接円をもち、外接円も持つことから双心四角形であることが分かります。
　
　直線 KL,LM,MN,NK の方程式を求めると、以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} {\mathrm{KL}}:\left( \frac{2ab^2}{a^2+b^2} - \frac{2b^2c}{b^2+c^2} \right)y-\left( \frac{2a^2b}{a^2+b^2} - \frac{2bc^2}{b^2+c^2} \right)x+\frac{4abc(a-c)}{a^2+b^2+c^2+d^2}=0 \\ {\mathrm{LM}}:\left( \frac{2b^2c}{b^2+c^2} - \frac{2cd^2}{c^2+d^2} \right)y-\left( \frac{2bc^2}{b^2+c^2} - \frac{2c^2d}{c^2+d^2} \right)x+\frac{4bcd(b-d)}{a^2+b^2+c^2+d^2}=0 \\ {\mathrm{MN}}:\left( \frac{2cd^2}{c^2+d^2} - \frac{2d^2a}{d^2+a^2} \right)y-\left( \frac{2c^2a}{c^2+a^2} - \frac{2da^2}{d^2+a^2} \right)x+\frac{4cda(c-a)}{a^2+b^2+c^2+d^2}=0 \\ {\mathrm{NK}}:\left( \frac{2d^2a}{d^2+a^2} - \frac{2ab^2}{a^2+b^2} \right)y-\left( \frac{2da^2}{d^2+a^2} - \frac{2a^2b}{a^2+b^2} \right)x+\frac{4dab(d-b)}{a^2+b^2+c^2+d^2}=0 \end{array} \end{eqnarray} $$
原点 O と直線 KL,LM,MN,NK のそれぞれの距離 $d_\mathrm{KL},\ d_\mathrm{LM},\ d_\mathrm{MN},\ d_\mathrm{NK}$は、先ほど求めた四角形 KLMN の各辺の長さを用いることで以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} d_\mathrm{KL}=\frac{\left| \frac{4abc(a-c)}{a^2+b^2+c^2+d^2} \right|}{\frac{2\left| b \right|\left| a-c \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}} \\ d_\mathrm{LM}=\frac{\left| \frac{4bcd(b-d)}{a^2+b^2+c^2+d^2} \right|}{\frac{2\left| c \right|\left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}} \\ d_\mathrm{MN}=\frac{\left| \frac{4cda(c-a)}{a^2+b^2+c^2+d^2} \right|}{\frac{2\left| d \right|\left| a-c \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}} \\ d_\mathrm{NK}=\frac{\left| \frac{4dab(d-b)}{a^2+b^2+c^2+d^2} \right|}{\frac{2\left| a \right|\left| b-d \right|\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}} \end{array} \end{eqnarray} $$
さらに整理すると以下のように表せます。
$$ \begin{eqnarray} \begin{array}{l} d_\mathrm{KL}=-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ d_\mathrm{LM}=-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ d_\mathrm{MN}=-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \\ d_\mathrm{NK}=-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2} \end{array} \end{eqnarray} $$
　
　したがって、原点 O から四角形 KLMN の４辺までの距離がいずれも $-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}$ であるため、点 O が内心であり、その半径は $-\frac{2ac\sqrt{a^2+b^2+c^2+d^2}}{a^2+b^2+c^2+d^2}$ であることが分かります。（４点 K,L,M,N はそれぞれ異なる象限にあるため、点 O は四角形 KLMN の内部にあります。）
　
　$\ $

〔Ⅲ〕３．の証明

　
　〔Ⅱ〕３．と〔Ⅲ〕２．より、双心四角形 KLMN の内心を点 O 、双心四角形 KLMN の対角線の交点を P 、双心四角形 KLMN の外心を点 Q と対応させることができるため、この３点が同一直線上にあることが分かります。
　
　$\ $

おわりに

　
　ここまで読んでいただきありがとうございました！この性質自体は１年半ほど前に気づいていたのですが、なかなか証明をできずにいました。所々厳密性に欠ける部分はあったかもしれませんが、今回この場を借りて性質の紹介・証明をできたことが嬉しいです。ただ、証明に自信がないので、誤りがある場合は教えていただけるとありがたいです。
　
　この性質は図形的に単純な条件であるので、既に誰かが見つけていると思われます（もし、初めてなのであれば「共有共円定理」と名付けたいです）。