1
高校数学問題
図形問題
195
0
$$$$
図1において,四角形$ABCD$,$ECFG$は正方形で,四角形$BHIG$は長方形です.
また,点$A,D,I$は一直線上,点$H,C,I$も一直線上にあります.
$EI = 2$のとき,線分$AG$の長さを求めてください.
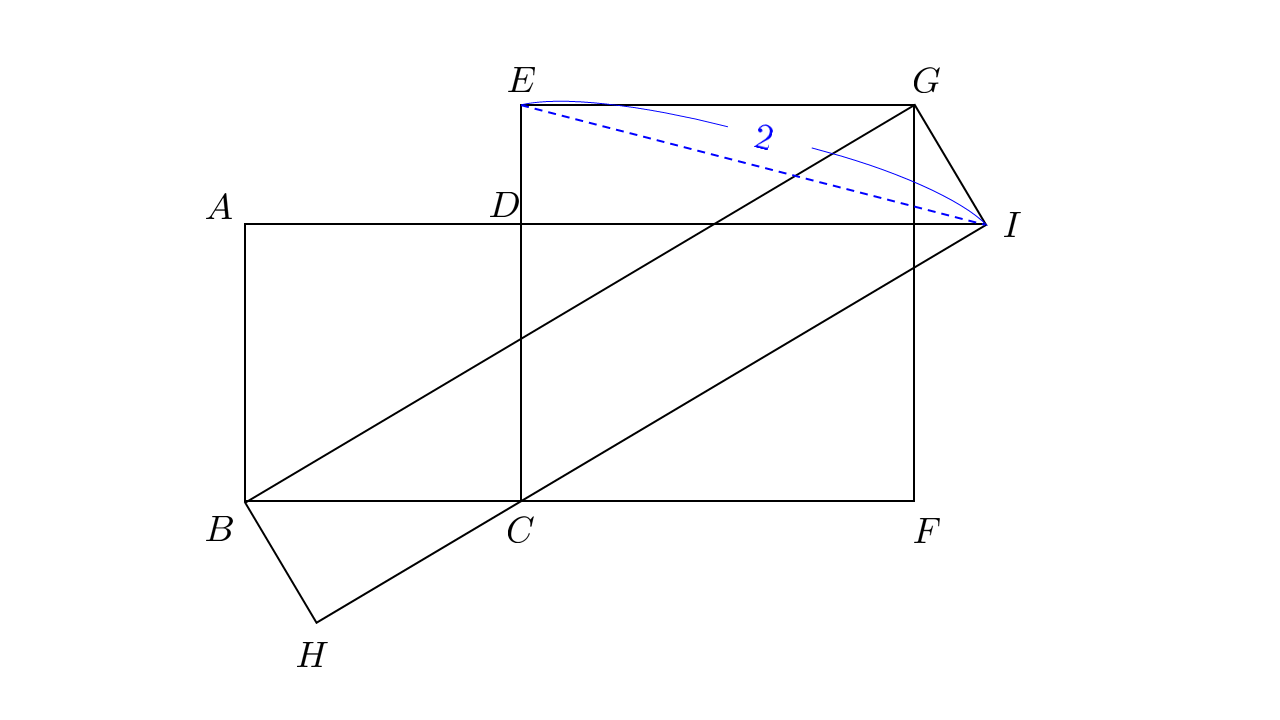
高校生の頃作った図形問題です.もっと簡単な解法が思い付いたら是非教えてください.
解答を表示
まず,正方形$ECFG$の外接円を描きます.

$\angle GIC = 90^{\circ}$より,この外接円は,四角形$ECIG$の外接円にもなります.
ここで,$EG = CE = L$, $GI = a$, $CI = b$とおくと,

$EI = 2$, $CG = \sqrt{2} L$より,トレミーの定理から,
$EC \cdot GI + EG\cdot CI = EI \cdot CG \Leftrightarrow La + Lb = 2\sqrt{2}L \Leftrightarrow a + b = 2\sqrt{2},$となります.
ここで,$C,G,I$を頂点に持つ長方形を考えると,面積は$ab$になります.
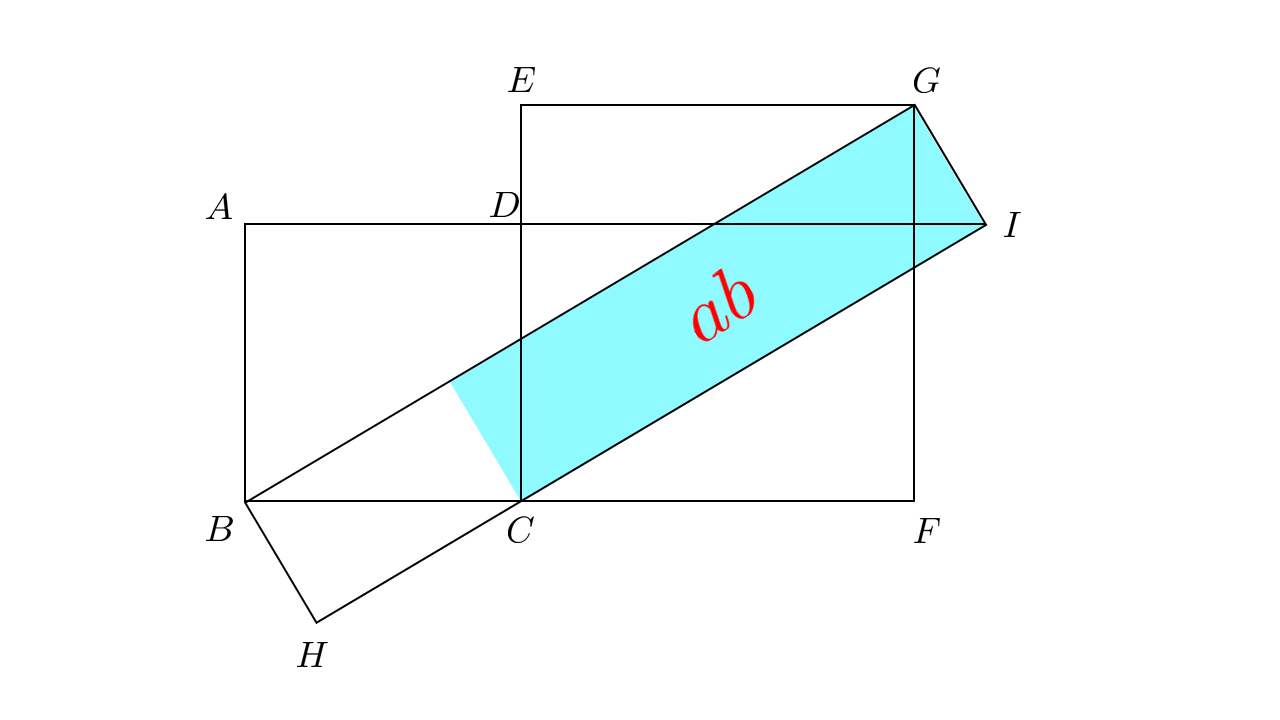
これを$B,C,I$を頂点に持つ平行四辺形に平行移動します.
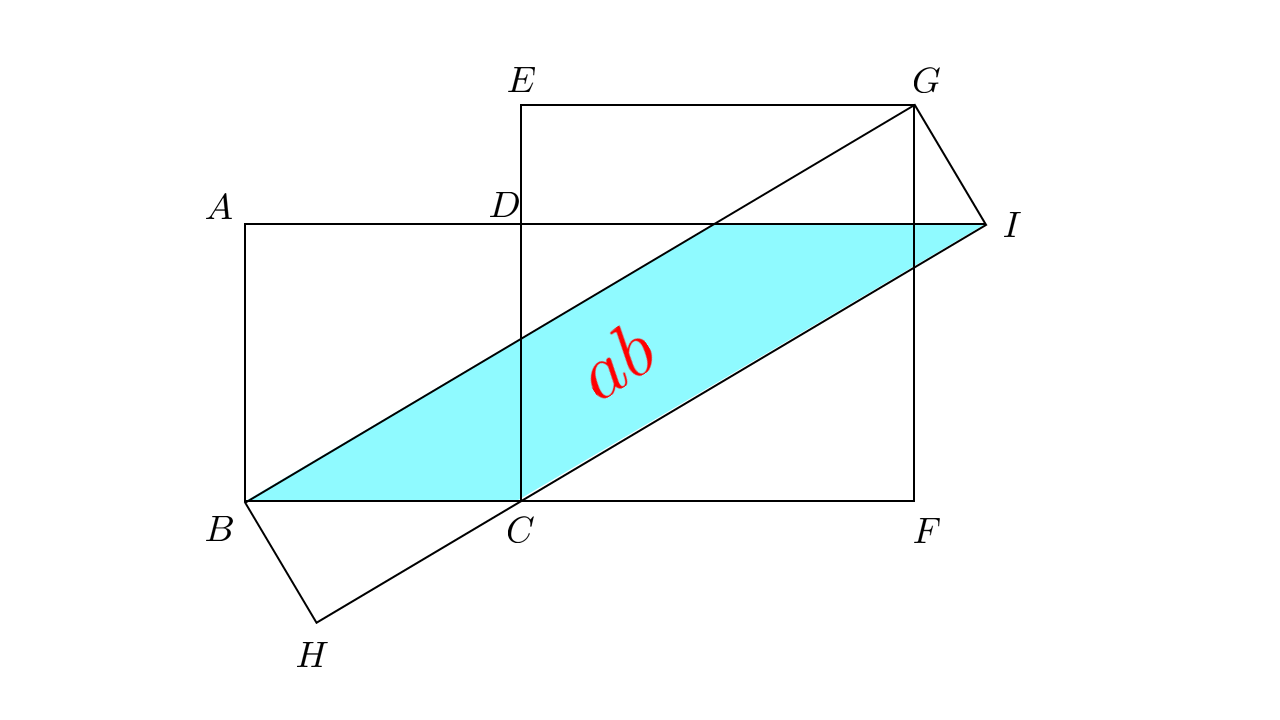
さらに,正方形$ABCD$に平行移動させると,平行移動を繰り返しただけなので,面積は変わらず$ab$となります.

したがって正方形$ABCD$の一辺の長さは$\sqrt{ab}$から,対角線の長さは$\sqrt{2ab}$となります.さらに$CG$の長さは三平方の定理から$\sqrt{a^2+b^2}$で,$\angle ACG = 90^{\circ}$なので,
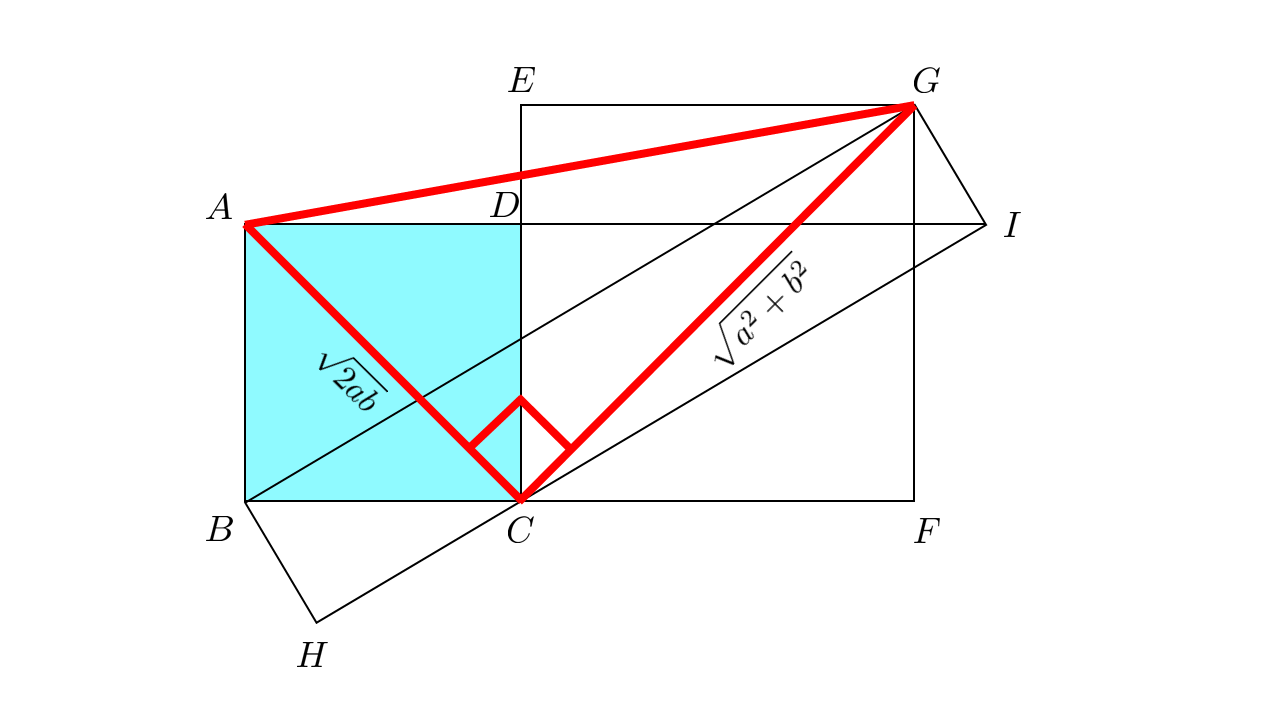
三平方の定理から,
$AG^2 = AC^2 + CG^2 = 2ab + a^2 + b^2 = (a+b)^2 $より,
$AG = a + b = 2\sqrt{2}$となります.
投稿日:2023年10月4日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
Mathお
56
8315
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中