3
高校数学解説
Apostolによる√2が無理数であることの図形証明
233
0
$$$$
Apostolによる√2が無理数であることの図形証明
25年前にApostolが見つけた$\sqrt2$が無理数であることの図形証明(文献[1])を紹介する. 非常にシンプルではあるがApostolの深い洞察力に驚かされる. Apostolの論文では「3辺が整数となるより小さな直角二等辺三角形がいくらでも作れるので矛盾」となっているが以下の言い回しの方が簡潔に見える.
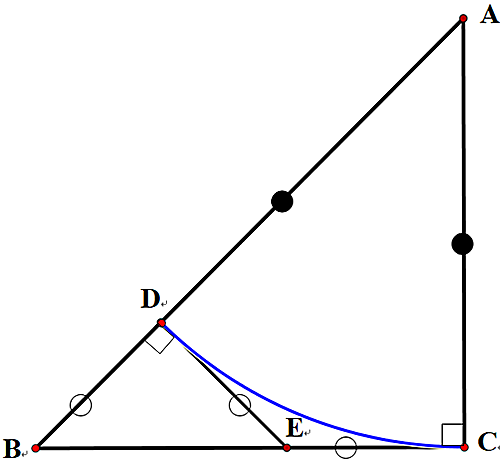
$\sqrt2$が有理数であると仮定すると直角二等辺三角形の3辺が整数比で表せる. いま, 3辺が整数となる最小の直角二等辺三角形$ABC$において, 下図のようにその内部に直角二等辺三角形$DBE$を作ると, これもまた3辺が整数となることがわかり, 直角二等辺三角形$ABC$の最小性に反し矛盾. ゆえに$\sqrt2$は無理数である.
(参考文献)
[1] T.M.Apostol, "Irrationality of the Square Root of Two — A Geometric Proof", American Mathematical Monthly 107.9(2000)
投稿日:2025年5月29日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中
